Ученический проект "Быстрые математики"

 

 

 

 

 

 

 

 

Проект

 

Быстрые математики.

 

 

 

 

 

 

 

 

Подготовили учащиеся 6Б класса

Видяпина Анастасия

Михайлов Дмитрий

 

Руководитель: учитель математики

Пастухова Н.А.

 

 

 

 

 

 

 

СОДЕРЖАНИЕ

ВВЕДЕНИЕ…………………………………………….………..……2

ОСНОВНАЯ ЧАСТЬ …………………………………………………

     1. История развития способов быстрых вычислений………………..3

2. Приемы устного счета………………………………….……………5

2.1.  сложение чисел

2.2.  вычитание чисел

2.3.  умножение чисел

2.4.  деление чисел

ЗАКЛЮЧЕНИЕ…….……………………………………………………8

СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ……………...……..9

ПРИЛОЖЕНИЯ………………………………………………………….10

 

Введение

На уроках математики намприходится производить разные вычисления.

Мне нравится программа «Удивительные люди». В ней  дети очень быстро считают, решают сложные примеры и задания. В моем классе некоторые одноклассники не очень хорошо и быстро считают, я решила им помочь.
Основополагающий вопрос: можно ли научиться быстрым вычислениям?
Гипотеза:
1) Быстрые вычисления доступны только «удивительным людям».
2) Можно овладеть приемами быстрого счета.

Известно, что производя математические вычисления в уме, человек выполняет настоящую интеллектуальную гимнастику, тренирует свои умственные способности, память.

У́стный счёт — математические вычисления, осуществляемые человеком без помощи дополнительных устройств (компьютер, калькулятор, счёты и т. п.) и приспособлений (ручка, карандаш, бумага и т. п.).

Счет в уме является самым древним способом вычисления. Знание приемов устных вычислений остается необходимым даже при наличии калькуляторов.  Устные вычисления дают возможность, произведя расчеты устно, контролировать, прогнозировать, оценивать возможные результаты при решении различных задач. А также, умение быстро считать устно поможет в жизни, чтобы не стать жертвами обмана на рынке или в магазине.

Поэтому, изучение приемов устного счета, позволяющие быстро и правильно производить в уме достаточно сложные вычисления, является актуальной темой.

Цель исследования: повысить вычислительную скорость через использование  приемов устного счета.

Задачи исследования:

1.      Познакомиться с историей развития  способов быстрых вычислений.

2.      Изучить приемы устного счета на примере арифметических действий с натуральными числами.

3.      Анализ и систематизация результатов диагностических работ.

На уроках математики вместе с учителем мы провели входную диагностику устного счета, состоящую из трех частей, после ее проведения мы знакомили одноклассников с приемами устного счета. Через некоторое время   диагностика была повторена, и результаты первоначального и повторного выполнения работы были сравнены. (Приложение 4 - 5).

 

 

 

 

 

 

 

Основная часть

1.                               История развития быстрых способов вычислений

Никто не знает, как впервые появилось число, как первобытный человек начал считать. Однако десятки тысяч лет назад первобытный человек, собирая плоды деревьев, охотясь  и занимаясь рыбной ловлей, научился считать различные предметы, с которыми он встречался в повседневной жизни. А решение многих важных жизненных вопросов привело к необходимости производить и различные вычисления.

Вначале человек научился выделять единичные предметы. Научившись выделять один предмет из множества других, древние люди говорили: "один", а если их было больше - "много". Частые наблюдения множеств, состоящих из пары предметов (глаза, уши, крылья, руки), привели человека к представлению о числе два. Постепенно человек научился считать до трех, затем до пяти и до десяти и т.д. Для счета люди использовали пальцы рук, ног. Ведь и маленькие дети тоже учатся считать по пальцам. Система счисления на основе десяти возникла как естественное развитие пальцевого счета.При помощи пальцев рук люди научились не только считать большие числа, но и выполнять действия сложения и вычитания.

По мере развития речи люди начали использовать слова для обозначения чисел и изображения чисел с помощью рисунков, чертежей или символов. Древние торговцы для удобства счета начали накладывать зерна и раковины на специальную дощечку, которая со временем стала называться абаком.

Особенно сложны и трудны были в старину действия умножения и деления - особенно последнее. «Умноженье - мое мученье, а с делением - беда», - говорили в старину. Известен старинный русский способ умножения на пальцах однозначных чисел от 6 до 9, он  издревле применялся купцами как вспомогательный при устном счёте. Первоначально пальцы обеих рук сжимали в кулаки. Затем на одной руке разгибали столько пальцев, на сколько первый множитель превосходит число 5, а на второй руке делали то же самое для второго множителя. Суммарное число вытянутых пальцев умножалось на 10, потом перемножалось число загнутых пальцев одной руки на число загнутых пальцев другой. Два полученных результата складывались. (Приложение 1). Также, используя пальцы рук, находили произведение чисел больше 2 на число 9. Повернув обе ладони к себе, загибали , считая слева, палец соответствующий множителю. Число пальцев слева от загнутого будет равно десяткам, а справа – единицам искомого произведения.(Приложение 2).

В книге В. Беллюстина «Как постепенно дошли люди до настоящей арифметики» (1914) изложено 27 способов умножения, причем автор замечает: «весьма возможно, что есть и еще (способы), скрытые в тайниках книгохранилищ, разбросанные в многочисленных, главным образом, рукописных сборниках».

Подробно разработанная система резкого повышения быстроты устного счета создана была в годы второй мировой войны цюрихским профессором математики Я. Трахтенбергом. Она известна под названием "Системы быстрого счета". История ее создания необычная. В 1941 году гитлеровцы бросили Трахтенберга в концлагерь. Чтобы уцелеть в нечеловеческих условиях и сохранить нормальной свою психику, Трахтенберг начал разрабатывать принципы ускоренного счета. За четыре страшных года пребывания в концлагере профессору удалось создать стройную систему ускоренного обучения детей и взрослых основам быстрого счета. После войны Трахтенберг создал и возглавил Цюрихский математический институт, получивший мировую известность.

      В России хорошо известна картина русского художника Николая Богданова-Бельского «Устный счёт. В народной школе С. А. Рачинского», написанная в 1895 году.

10 2 + 11 2 + 12 2 + 13 2 + 14 2 365 {\displaystyle {\frac {10^{2}+11^{2}+12^{2}+13^{2}+14^{2}}{365}}} На картине изображена деревенская школа конца XIX века во время урока арифметики при решении дроби в уме. Учитель — реальный человек, Сергей Александрович Рачинский (1833—1902), ботаник и математик, профессор Московского университета. На волне народничества в 1872 году Рачинский вернулся в родное село Татево, где создал школу с общежитием для крестьянских детей, разработал уникальную методику обучения устному счёту, прививая деревенским ребятишкам его навыки и основы математического мышления. Эпизоду из жизни школы с творческой атмосферой, царившей на уроках, и посвятил своё произведение Богданов-Бельский, сам в прошлом ученик Рачинского. (Приложение 3)

Существует достаточное количество математических книг и упражнений, обучающих секретам быстрого устного счета. Скорость и точность вычислений не являются особенным даром или талантом, их можно развить ежедневными упражнениями.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2. Приемы устного счета

2.1 Приемы быстрого сложения

Чтобы прибавить к числу 9, прибавьте к нему 10 и отнимите 1; чтобы прибавить 8, прибавьте 10 и отнимите 2; чтобы прибавить 7, прибавьте 10 иотнимите3 и т.д.

Пример: 56+8=56+10-2=64;

                 65+9=65+10-1=74.

1.Округление

Если слагаемые близки к круглым числам, то их заменяют разностью или суммой между круглым числом и дополнением числа до десятка. прием Пример: 3916+991=3916+1000-9=4916-10+1=4907;

                 399+473=(400 – 1)+473=872

 Этот прием можно использовать во всех четырех арифметических действиях

Пример: 35·18=35·20-35·2=700-70=630;

                596:4=600:4-4:4=150-1=149

2 . Переместительного и сочетательное свойства сложения (умножения)

Пример: 72 + 63 + 28 = 72 + 28 + 63 = 163;

                 25·37·4=25·4·37=3700.

Известен исторический пример использования этих свойств. Восьмилетний мальчик – будущий немецкий математик Карл Гаусс, поразил учителя, сосчитав необычным образом сумму натуральных чисел от 1 до 100: он сообразил, что сумма пар чисел, равноудаленных от концов, одинакова:

 1 + 100 = 2 + 99 = 3 + 98 =... = 50 + 51 = 101, и что таких пар ровно 50,поэтому искомая сумма равна 101·50 = 5050.

 

2.2  Приемы быстрого вычитания

1. Вычитание путем округления уменьшаемого или вычитаемого

При вычитании 9 из любого числа из него вычитают 10 и добавляют 1;
при   вычитании 8 из любого числа из него вычитают 10 и добавляют 2.

Пример:321-9=321-10+1=312;     321-8=321-10+2=313;     

 321-17=321-20+3=304;  302 – 75 = 300 – 75 + 2 = 227.

 

2 .Вычитание путем уравнивания числа единиц последних разрядов уменьшаемого.

Пример: 67 – 48 = 68 – 48 – 1=19

Добавив к уменьшаемому 1, вычитаем 48 из 68, получаем 20. Отняв от этой разности ранее добавленную единицу, окончательно получаем 19.

 

2.3  Приемы быстрого умножения

1. Умножение на 9.

Любые числа умножаются на 9 легко и просто: следует умножить заданное число на 10 (или просто приписать ноль), а от полученного числа отнять исходное: 

Пример: 63 · 9=630–63=567

 

2. Умножение на 5, на 50.

Чтобы умножить число на 5, нужно умножить его на 10 и разделить на 2 (или в другой последовательности).

Пример: 17·5=17·10:2=170:2=85

Чтобы умножить число на 50, нужно умножить его на 100 и полученное произведение разделить на 2.

Пример: 43·50=43·100:2=4300:2=2150

 

3.Умножение на 25; на 125.

Чтобы умножить число на 25, нужно умножить его на 100 и полученное произведение разделить на 4.

 Пример: 27·25=27·100:4=2700:4=675.

Чтобы умножить число на 125, нужно умножить его на 1000 и полученное произведение разделить на 8.

Пример: 96·125=96:8·1000=12000.

 

4.Умножение на 15.
При умножении на 15, если число нечетное, умножают его на10 и прибавляют половину полученного произведения:
23·15=23·10 + 230 : 2=230+115=345;
если же число четное, то к числу прибавляем его половину и результат умножаем на 10:
18·15=(18+9)·10=27·10=270.

5.Умножение на число, записанное одними девятками.
Для того, чтобы найти произведение числа, написанного одними девятками, на число, имеющее с ним одинаковое количество цифр, надо от множителя отнять единицу и к получившемуся числу приписать другое число, все цифры которого дополняют цифры получившегося числа до 9.
Пример: 8·9=72;
                 46·99=4554;
                 137·999=136 863;
                 3562·9999=35616438.
Наличие такого способа усматривается из следующего приёма решения приведённых   примеров:

8·9=8·(10–1)=80–8=72,

 46·99=46·(100–1)=4600–54=4554.

 

6.Умножение на 11.

Следует “раздвинуть” цифры числа, умножаемого на 11, и в образовавшийся промежуток вписать сумму этих цифр, причем если эта сумма больше 9, то, следует единицу перенести в старший разряд:

Пример: 34·11=374, т.к. 3+4=7 , семерку помещаем между тройкой и четверкой;

68·11=748, т.к. 6+8=14 , четверку помещаем между семеркой (шестерка плюс перенесенная единица) и восьмеркой.

 

7.Умножение чисел, близких к 100 и 1000.

Умножаем число на 100 (на 1000) и вычитаем произведение этого числа на дополнение второго множителя до 100 (до 1000).

Пример: 245·98=245· (100-2)=24500 – 490 =24010

                 375·999=375· (1000-1)=375 000 - 375 = 374 625

 

8.Умножение на 22,33,……99.

Чтобы умножить двузначное число на 22, 33,…,99 надо этот множитель представить в виде произведения однозначного числа (от 2 до 9) на 11, затем произведение первых двух чисел умножить на 11.

24·22 = 24·(2·11)= (24·2)·11= 48·11=528

23·33=23·3·11=69 ·11=759

 

9.Возведение в квадрат чисел, оканчивающихся на 5.

85²=7225

Шаг 1 – умножить цифру десятков на следующую за ней цифру:

8 · (8+1)=72

Шаг 2 – дописываем к получившемуся результату 25:   7225

 

10.Умножение двухзначного числа на 101.

Припишите ваше число к самому себе. Умножение закончено.

Пример: 57·101=5757

 

11.Умножение двузначных чисел на 111.
Например, 45·111
Так как 111=100+10+1, то 45·111=45·(100+10+1). 
 При умножении двузначного числа на 111, сумма цифр которого меньше 10, надо в середину между цифрами вставить два раза сумму цифр (т.е. чисел, ими изображаемых) его десятков и единиц 4+5=9.   4500+450+45=4995.

  Следовательно, 45·111=4995.

 

2.4 Приемы быстрого деления

1.Деление на 5, 50 и 25.

Чтобы число разделить на  5; 50 или 500, надо это число разделить на 10; 100 или 1000 соответственно, и затем результат умножить на 2 (или в другом порядке)

Пример: 315 : 5=315 ∙ 2 : 10=630 :10= 63;
                 3750 : 50=3750 ∙ 2 :100=7500 :100=75;
                 6400 : 25=6400 :100 ∙ 4 = 64 ∙ 4  = 256;
                 21600 : 50 = 21600 : 100 · 2 = 432.( 10 ⋅ N + 5 ) ⋅ ( 10 ⋅ N + 5 ) = 10 2 ⋅ N 2 + 2 ⋅ 5 ⋅ 10 ⋅ N + 5 2 = 100 ⋅ N 2 + 100 ⋅ N + 25 = 100 ⋅ N ( N + 1 ) + 25 {\displaystyle (10\cdot N+5)\cdot (10\cdot N+5)=10^{2}\cdot N^{2}+2\cdot 5\cdot 10\cdot N+5^{2}=100\cdot N^{2}+100\cdot N+25=100\cdot N(N+1)+25} A 2 = ( A + d ) ( A − d ) + d 2 {\displaystyle A^{2}=(A+d)(A-d)+d^{2}}

Заключение

Рассмотренные методы устного счета доступны для каждого человека и являются своеобразной гимнастикой для ума.  Сравнительный анализ результатов диагностической работы показал, что скорость и точность вычислений не являются особенным даром или талантом, их можно развить ежедневными упражнениями.  ( Приложение 5). Считаю, что математика не только точная наука, но и очень интересная. Благодаря данному исследованию, мой интерес, и думаю, интерес моих одноклассников к математике еще больше повысился.

Конечно, невозможно применять все существующие способы и приемы быстрого устного счета, так как их достаточно много, и чтобы изучить все требуется большое количество времени, но выбрать для себя самые практичные и полезные может каждый человек.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Литература

1. Кордемский Б.А., Ахадов А.А. Удивительный мир чисел: Книга для учащихся, - М. Просвещение, 1986.

2. Г.Н. Берман. Приемы быстрого счета, - ОГИЗ, Государственное издательство технико-теоретической литературы, 1947, Ленинград.

3. Я.И. Перельман «Занимательная арифметика» – М, Транзиткнига, 2005.

4. Бикташева Л. В. Алгоритмы ускоренных вычислений \ Камаев П. М. (сост.) Устный счет.  – М.: Чистые пруды, 2007. – 32 с. – (Библиотечка «Первого сентября», серия «Математика». Вып. 3(15)).

5.https://ru.wikipedia.org/wiki/%D0%A3%D1%81%D1%82%D0%BD%D1%8B%D0%B9_%D1%81%D1%87%D1%91%D1%82

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Приложение 1

Способ быстрого умножения чисел в пределах первого десятка чисел больших 5.

Например, умножим 7 на 8. В рассмотренном примере будет не загнуто 2 и 3 пальца. Если сложить количества не загнутых пальцев (2+3=5), затем умножить эту сумму на 10 и перемножить количества загнутых (2•3=6), то

получатся соответственно числа десятков и единиц искомого произведения 56.

 

 

 

 

 

 

 

 

 

 

 

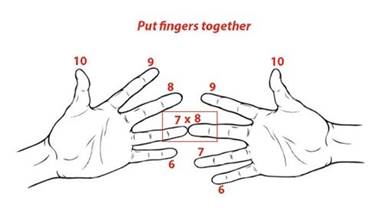Приложение 2

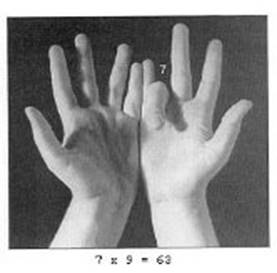Способ быстрого умножения чисел в пределах первого десятка на 9. Например, умножим 7 на 9. Повернём руки ладонями к себе и загнём седьмой палец (начиная считать от большого пальца слева). Число пальцев слева от загнутого будет равно десяткам - 6, а справа – единицам искомого произведения – 3.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Приложение 3

 

 

«Устный счет. В народной школе С.А. Рачинского».

Николай Богданов – Бельский, 1895г.

 

 

 

 

 

 

 

 

 

Приложение 4

 

Входная диагностика  №1

1.     3907 + 39 +993

2.     2567 + 9

3.     598 + 225

4.     747 - 349

5.     403 – 76

6.     1 + 2 + 3 + …+200

 

Входная диагностика  №2

7.     64 ∙ 25

8.      47 ∙ 5

9.      57 ∙ 11

10.  43 ∙ 22

11.  63 ∙ 101  

12.  43 · 15   

 Входная диагностика  №3

 

13.  25 ∙ 25

14.  43 ∙ 111

15.  47 · 99

16.  235 : 5

17.  1350 : 50

18.  2100 : 25

Приложение 5.

Правильно выполнили (кол-во учащихся) задания входной  (синие столбики) и повторной диагностики (красные столбики).

 

Диагностика 1.

 

 

Диагностика 2.

 

 

Диагностика 3.

 

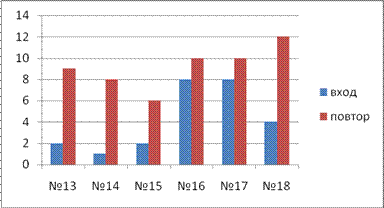
Скачано с www.znanio.ru