Урок алгебры по теме : " Решение линейных неравенств" 8 кл

МКОУ «Аджидадинская СОШ» Кумторкалинского  района

Открытый урок   по математике

На тему :

«Решение  линейных  неравенств »

8 класс

Провела учитель математики :

Эльдарханова М.А

2021г

Решение линейных неравенств

У р о к  1

Цели: объяснить правило решения и оформления решения линейных неравенств; формировать умение решать линейные неравенства.

Ход урока

I. Организационный момент.

II. Анализ самостоятельной работы.

На доске рассмотреть задания, по которым было допущено наибольшее количество ошибок. Учащимся, не справившимся с данной работой, домой дается работа, содержащая аналогичные задания.

1) Известно, что a < 3. Какой знак имеет следующее выражение:

а) 12a – 4;     б) (a – 1)2(a – 3);     в)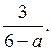

2) Докажите, что если a > 5, то 3a – 7 > 8.

3) Докажите, что при любых значениях переменной верно неравенство 14y – 49 ≤ y2.

III. Объяснение нового материала.

Учащиеся вспоминают понятие линейных уравнений. Учитель вводит понятие линейных неравенств, формулирует правила решения данных неравенств, показывает на координатной прямой множество решений данных неравенств:

а) x – 3 > 0;          б) 2x + 5 < 7.

IV. Закрепление нового материала.

1) На координатной прямой показать множества решений неравенств:

x > 8; x < –5; x ³ 2; x £ –2; x > 0,1.

2) Рассмотреть решение неравенств № 33.1; 33.4; 33.6; 33.9; 33.11; 33.13.

3) Найдите   наименьшее   целое   значение,   удовлетворяющее   неравенству:

а) 2x + 13 > 57;                б) 5x – 14 > 1; в) 3x + 8 > 2.

4) Найдите наибольшее целое число, удовлетворяющее неравенству:

а) 5x – 6 < 14;                  б) 7x + 1 < –20.

V. Подведение итогов.

Домашнее задание: изучить материал параграфа 33, выучить правила. Решить задачи № 33.3; 33.5; 33.8; 33.10.

У р о к  2

Цели: повторить правила решения линейных неравенств; рассмотреть решение линейных неравенств различного уровня сложности; развивать умение  решать  неравенства  и  показывать  решение  на  координатной прямой.

Ход урока

I. Организационный момент.

II. Индивидуальная работа.

К доске вызываются четыре ученика, которые самостоятельно выполняют задания с карточек:

III. Актуализация знаний.

Во время проведения индивидуальной работы остальные учащиеся устно решают следующие неравенства:

2x > 24;  5x < –15;  –3x > 21;  10x < –30;  –2x < –16.

Затем выполняют № 33.2; 33.12; 33.25 (б).

IV. Решение задач.

1) Решаются неравенства № 33.15; 33.17; 33.19; 33.21; 33.30 (а, б).

2) Найдите наибольшее целое значение переменной x, удовлетворяющей неравенству:

а) 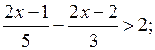     б)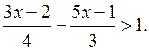

3) Найдите наименьшее целое x, удовлетворяющее неравенству:

а) 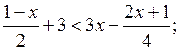     б)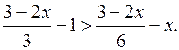

4) С  сильными  учениками  разобрать  решение  следующего  неравенства:

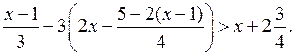
Р е ш е н и е:

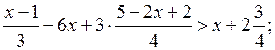
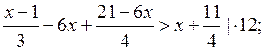
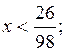
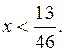
О т в е т: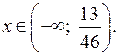

V. Подведение итогов.

Домашнее задание: решить задачи № 33.16; 33.18; 33.23; 33.25 (в).

У р о к  3

Цели: рассмотреть решения неравенств различной сложности, а также решение задач, с помощью неравенств; развивать умение решать линейные неравенства.

Ход урока

I. Организационный момент.

II. Индивидуальная работа.

К доске вызываются ученики выполнить задания с карточек:

III. Актуализация знаний.

Пока выполняются задания с карточек, остальные учащиеся по вариантам решают самостоятельно № 33.20.

По  прошествии  некоторого  времени  проверяются  задания  на  доске, с полным объяснением, задания в тетрадях, а так же номера домашней работы.

IV. Решение задач.

1) Разобрать решение заданий № 33.28 (а, б); 33.29; 33.31; 33.35; 33.38.

2) Рассмотреть решение дробных неравенств:

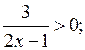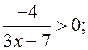а)      б)      в)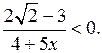

Решение данных неравенств происходит по алгоритму:

1) определить знак числителя;

2) по знаку неравенства и знаку числителя составить неравенство для знаменателя;

3) решить получившееся неравенство.

3) Сильным ученикам предложить рассмотреть решение сложного неравенства:

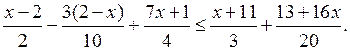
Р е ш е н и е:

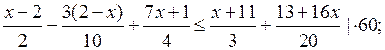
85x ≤ 340;

 x ≤ 4.

О т в е т: (–∞; 4].

V. Самостоятельная работа.

Окончание табл.

О т в е т ы:

VI. Подведение итогов.

Домашнее задание: решить задачи № 33.27 (б, г); 33.30 (в, г); 33.35