Урок алгебры "Решение систем уравнений второй степени" 9 кл

 

 

 

 

 

Открытый урок по алгебре

в 9 классе.

 

 

Тема урока:  

 

Решение систем уравнений     второй степени с двумя методом подстановки.

 

 

 

 

 

 

 

 

 

 

 

Цели урока:

Обучающие:

·       систематизировать знания по данной теме

·        выработать умение решать системы уравнений, содержащие уравнения второй степени  способами подстановки.

Развивающие:

·       развивать вычислительную технику, мыслительную  активность,  логическое мышление;

·         способствовать формированию ключевых понятий;

·        выполнять задания различного уровня сложности; развивать правильную математическую речь

·        формировать графическую и функциональную  культуру  обучающихся.

Воспитывающие:

·       воспитывать внимательность, аккуратность, умение четко организовывать самостоятельную и индивидуальную работу, воспитывать глубокий и  устойчивый интерес к изучению математики

·       формировать навыки общения, умения работать в коллективе.

Задачи   урока:

         1. Отработать  алгоритм  решения  систем уравнений второй степени способом подстановки  и  различного  уровня  сложности.

         2. Отработать  навыки  и  умения  иллюстрировать  решения систем уравнений   графически. 

Формы работы на уроке: фронтальная, индивидуальная, коллективная, групповая,     самостоятельная, работа в парах.

    Тип урока: комбинированный.

 

 Методы урока: практический,  наглядный,  словесный.

 

Оборудование: учебник «Алгебра – 9 класс» Макарычева Ю.Н., под ред. С.А.Теляковского,  раздаточный  материал, карточки с алгоритмом портреты.

 

 

 

 

 

 

 

Ход урока.

 

I.      Организационный момент

Математике должны учить в школе

еще с той целью,

чтобы познания, здесь приобретаемые,

были достаточными для обыкновенных

 потребностей в жизни.

И.Л. Лобачевский 

 

       Сегодняшний урок я хотела начать с философской загадки   «Что самое быстрое, но и самое медленное, самое большое, но и самое маленькое, самое продолжительное и краткое, самое дорогое, но и дёшево ценимое нами?»                (Время).

        Итак, у нас всего 45 минут, и мне очень хотелось, чтобы это время пролетело для вас незаметно и с пользой.

 Сегодня на уроке мы должны рассмотреть  способ подстановки  для решения систем уравнений.

 

II.  Проверка домашнего задания.

III  Актуализация опорных знаний.

Устный опрос.

1.

·       Определение системы уравнения с двумя переменными.

(Уравнения, объединенные фигурной скобкой, имеющие множество решений одновременно удовлетворяющих для каждого уравнения)

·       Что называют решением системы уравнений с двумя переменными?

(Пара значений, которые обращают каждое уравнение в системе в верное равенство)

·       Какие уравнения называются равносильными?

(Уравнения, которые имеют  одно и тоже множество решений   )

·       Назовите основные способы решения систем уравнений.

·       Графический, метод подстановки, метод алгебраического сложения, метод замены переменной.

 

2.

Учащиеся определяют вид уравнения, формулируют определения).

 

Решить уравнения:

1)                                     6) ,

2)  ,                                  7) ,

 

3)  ,                               8)

 

4)  ,                                 9)

 

5)                             10)       

 

3. Какая фигура является графиком уравнения?

   1) 3х-у=7;                                               

   2) ху=4;                                         

   3) у-х²+2х=0;                                 

 4)(х-2)²+у²=25.

 

4.Какая из следующих пар чисел является  решением системы уравнений

                                   х ²+у²=1

                                     у-2х=1

 

              (0;1)          (-1;-1)       (1;0)           (1;1)

5.  Решение какой системы изображено

 

 

 

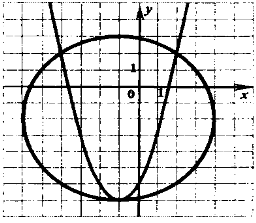
IV   Из истории решения систем уравнений.

                     ( Сообщение учеников)

     Еще древним вавилонянам и египтянам было известно много задач, решение которых сводилось к решению уравнений с одной переменной. Только в то время не умели применять в математике буквы. Поэтому вместо букв брали числа, показывали на числах, как решать задачу, а потом уже все похожие на нее задачи решали тем же способом.
       В древневавилонских текстах, написанных в III – II тысячелетиях до н.э., содержится немало задач, решаемых с помощью составления систем уравнений, в которые входят и уравнения второй степени.

    Многие уравнения умел решать греческий математик Диофант, который даже применял буквы для обозначения неизвестных.

   Но по-настоящему метод уравнений сформировался в руках арабских ученых. Они, по-видимому, знали, как решали задачи в Вавилоне и Индии, улучшили эти способы решения и привели их в систему. Первым написал книгу на арабском языке о решении уравнений Мухаммед ибн Мусса ал-Хорезми.    Название у нее было очень странное − «Краткая книга об исчислении ал-джабры и ал-мукабалы». В этом названии впервые прозвучало известное нам слово «алгебра».

   Книга ал-Хорезми о решении уравнений не была столь распространена, как его сочинение об индийском счете. Но и с нею познакомились математики Западной Европы. Когда они овладели методами ал-Хорезми, то стали их улучшать, применять к все более сложным уравнениям, настолько сложным, что без букв оказалось невозможно к ним подступиться.

   Французский ученый Франсуа Виет(XVIв.) впервые ввел символическую запись уравнения: стал обозначать неизвестные величины одними буквами, а известные − другими.    Алгебраическая символика совершенствовалась в трудах Декарта, Ньютона, Эйлера.

 

Рене Декарт
(1596 - 1650)
французский математик и философ

Мыслю, следовательно существую.

 

 

 

 

Исаа́к Нью́то́н 4 января 1643 — 31 марта 1727— английский физик, математик и астроном, один из создателей классической физики. Автор фундаментального труда «Математические начала натуральной философии», в котором он изложил закон всемирного тяготения и три закона механики, ставшие основой классической механики. Разработал дифференциальное и интегральное исчисление, теорию цвета и многие другие математические и физические теории.

 

 

ЛЕЙБНИЦ (Leibniz) Готфрид Вильгельм (1 июля 1646, Лейпциг - 14 ноября 1716, Ганновер), немецкий философ, логик, физик, математик и языковед.

 

 

 

 

 

 

Леонард Эйлер (1707—1783), — российский, немецкий и швейцарский математик. Анализировал бесконечно малые. Благодаря его работам, математический анализ стал вполне оформившейся наукой.

 

 

Карл Гаусс (1777—1855), — немецкий математик, астроном и физик. Создал теорию «первообразных» корней, из которой вытекало построение семнадцатиугольника. Один из величайших математиков всех времён.

Жозе́ф Луи́ Лагра́нж (25 января 1736 — 10 апреля 1813) — французский математик и механик итальянского происхождения. Наряду с Эйлером — лучший математик XVIII века. Особенно прославился исключительным мастерством в области обобщения и синтеза накопленного научного материала.

 

     

  Основная цель при решении систем линейных уравнений - решить систему уравнений, то есть найти все ее решения или доказать, что решений нет. Для решения системы уравнений с двумя переменными используются разные способы. Практическое применение этих способов - это решение задач, по алгебре, физике, химии, геометрии.

V. Изучение нового материала

     Основными методами решения систем уравнений являются метод подстановки и метод сложения.   

     При этом используют приемы: замена переменных, формулы сокращенного умножения, равенство произведения нулю и другие.

Записать на доске 3 метода решения систем уравнений.

 

        1. Графический метод

        2. Метод подстановки

        3.Метод алгебраического сложения

  

       С системами уравнений мы познакомились в курсе алгебры 7-го класса, но это были системы специального вида – системы двух линейных уравнений с двумя переменными.

      Алгоритм, который был выработан в 7 классе, вполне пригоден для решения систем любых двух уравнений с двумя переменными х и у.

1.     Выразить одну переменную через другую из одного уравнения системы.

2.     Подставить полученное выражение вместо переменной в другое уравнение системы.

3.     Решить полученное уравнение относительно одной переменной.

4.     Подставить поочередно каждый из найденных на 3 шаге корней уравнения в выражение, полученное на первом шаге и найти другую переменную.

5.     Записать ответ в виде пар значений (х;у).

Покажу, как работает этот метод при решении систем.

Решим систему уравнений: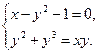

Применим метод подстановки. Преобразуем исходную систему:

           

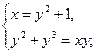
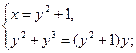
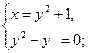
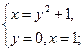
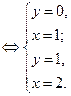                   Ответ: (1;0), (2;1)

VI. Закрепление знаний.

1.     Рассмотреть по учебнику      № 433( а), № 437 (а)

 

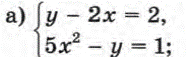
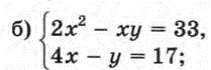
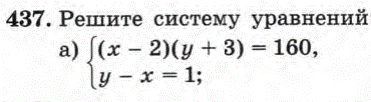
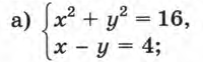
2.    Решение системы уравнений по алгоритму.

 

Реши систему уравнений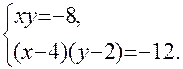 

 

                           Средь алгоритмов правильный найди,

И выбор свой подробно поясни!

 

 

 

 

 

 

 

 

 

 

 

 

 

Алгоритм А.                                                  Алгоритм В.

                                        

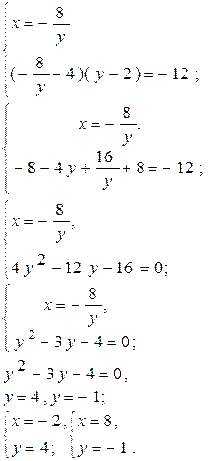
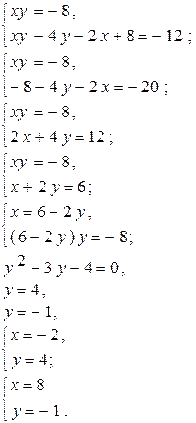
Ответ: (-2;4), (8;-1).                                          Ответ: (-2;4), (8;-1).                            

 

 

 

 

Алгоритм В.                                            Алгоритм Г.                                                                                                          

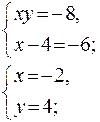
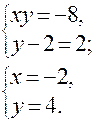
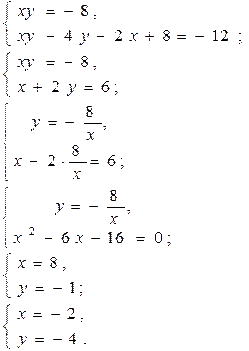
Ответ: (-2;4).                                                          Ответ: (-2;4), (8;-1).                            

 

3.     Тест с взаимопроверкой

Вариант 1

1. Какая из перечисленных пар является решением системы уравнений

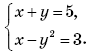
А. (1; 4).                Б. (4; 1).                    В. (–1; 4).                  Г. (–4; 1).

2. Из каких уравнений можно составить систему уравнений, решением которой будет пара чисел (1; 0)?
  А. xy = 4.                Б. 5x + y = 8.             В. 4x + y = 4.         Г. x² + y² = 1.

3. Сколько решений имеет система уравнений

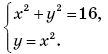
А. Одно.                     Б. Два.                  В. Три.       Г. Четыре.

4. Решение какой системы уравнений изображено на рисунке?

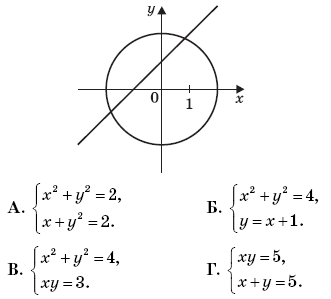
5. Решите систему уравнений

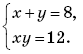
А. (2;6).                   Б.(6;2).           В.(2;6)и(6;2).                Г. (–2; –6) и (–6; –2).

Вариант 2

1. Какая из перечисленных пар является решением системы уравнений

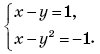
А. (3;2).                      Б.(2;3).                         В.(–3;2).                   Г. (–2; 3).

2. Из каких уравнений можно составить систему уравнений, решением которой будет пара чисел (0;1)?
А. 5x–4y=3.                    Б.7x+2y=2.                В.x² +y² =1.           Г. xy = 7.

3. Сколько решений имеет система уравнений

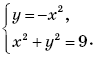
А. Одно.                   Б.Два.                    В.Три.               Г. Четыре.

4. Решение какой системы уравнений изображено на рисунке?

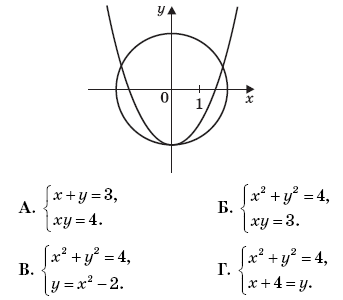
5. Решите систему уравнений

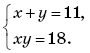
А. (2;9).               Б.(9;2).                        В.(9;2)и(2;9).             Г. (–9; –2) и (–2; –9)

ОТВЕТЫ К ТЕСТ

№	Вариант 1	Вариант 2
1	Б	А
2	В,Г	Б,В
3	Б	Б
4	Б	В
5	В	В

 

4.     Дифференцированный контроль

(взаимопроверка, работа )

На «3»   

 

 

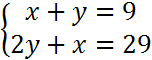
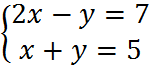
На «4»

 

 

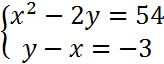
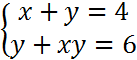
На «5»

 

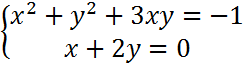
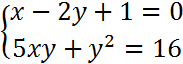
          VII. Домашнее задание  

По учебнику     п.19, стр.112

                              № 436, 441

VIII. Итог урока.

  Учащимся предлагается рисунок (у каждого на парте приготовлена заготовка), на котором нужно отметить свое местоположение для данного урока, т.е.:

 

 

Ø Если мало чего понятного и придется разбираться ещё раз с этим материалом, то вы у подножья горы;

Ø Если все предельно понятно, но вы не уверены в своих силах, то вы на пути к вершине;

Ø Если нет никаких вопросов и вы чувствуете власть над данной темой, то вы на пике.

    Говорят, что математика – гимнастика ума, я надеюсь, что сегодняшний урок был  для вас хорошей тренировкой, которая позволила стать более внимательными, собранными, сообразительными, заставила думать и творить что-то новое.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Скачано с www.znanio.ru