Урок геометрии в 8 классе "Решение задач с помощью метода вспомогательной площади"

Учитель Дудченко С.В.

Предмет. Геометрия

Класс 8

Урок № 40

Дата 12.02.2024

Тема. Решение задач с помощью метода вспомогательной площади

Цель: способствовать формированию умений решать задачи на вычисление площадей фигур, применяя различные методы, в том числе метод вспомогательной площади.

Задачи.

Предметные. Повторить формулы площадей многоугольников, свойства площадей. Систематизировать знания о методах решения задач на вычисление площадей. Учить детей решать задачи методом вспомогательной площади. Находить площади фигур на клетчатой бумаге. Решать задачи практического содержания. Обратить внимание детей применение знаний вычисления площадей фигур в различных отраслях.

Развивающие. Способствовать развитию логического мышления, математической речи, внимания, памяти.

Воспитательные. Воспитывать познавательный интерес к предмету, к поисковым решениям, культуру поведения при фронтальной и индивидуальной и групповой работе.

Планируемые результаты

Предметные умения: знать формулы площадей, уметь применять свойства площади, выбирать методы для решения задач, видеть разные способы для решения одной и той же задачи.

Метапредметные УУД:

познавательные: формулировать ответы на вопросы, используя учебник, свой жизненный опыт и информацию, полученную на уроке;

регулятивные: проговаривать последовательность действий, планировать действия в соответствии с поставленной задачей, вносить необходимые коррективы в действие после его завершения на основе его оценки и учета характера сделанных ошибок, высказывать свое предложение;

коммуникативные: уметь оформлять свои мысли в устной форме, слушать речь других, понимать и принимать их точку зрения, оценивать высказывания одноклассников, распределять обязанности при работе в паре, формулировать высказывания, задавать вопросы.

Личностные УУД: проявлять интерес к предлагаемой деятельности, изучению предмета, активность при решении задач, уважительное отношение к людям и результатам их деятельности.

Тип урока. Комбинированный урок.

Формы организации познавательной деятельности обучающихся: фронтальная, индивидуальная, групповая.

Образовательные ресурсы: учебник, презентация, поле кроссворда, бланки с фигурами для самостоятельной работы.

Ход урока.

І. Организационный момент

Приветствие, проверка готовности к уроку.                       

ІІ. Постановка цели урока. Мотивация учебной деятельности.

В повседневной жизни человек регулярно сталкивается с понятием площади в архитектуре, дизайне, спорте, строительстве и ремонте (поклейка обоев, укладка плит, паркета, линолеума), оплате услуг ЖКХ (расчет квартплаты осуществляется согласно общей площади квартиры), покупка и продажа земельных участков и так далее. Задачи на вычисление площадей встречаются в повседневной жизни, на контрольных и экзаменах.

Раз эта тема так важна, давайте вспомним методы решения задач на вычисление площадей многоугольников.

1.     Если можем сразу применить известную формулу, то такой метод называется… (Метод непосредственного применения формул)

2.     Если делим фигуру на части, вычисляем площади частей, а затем складываем полученные площади. Это метод… (Сложения площадей)

3.     Достраиваем фигуру до прямоугольника. Из площади прямоугольника вычитаем площади прямоугольных треугольников или других фигур. Это метод… (Достроения до прямоугольника)

4.     Использование формулы для многоугольников, вершины которых расположены в узлах сетки. Эта формула связывает площадь с количеством узлов, лежащих внутри и на границе многоугольника… (Формула Пика)

5.     Метод состоит в применении различных свойств площадей для составления соотношений, связывающих данные задачи и неизвестные, или использование известных площадей, для нахождения искомых?

Это и будет тема нашего урока. Запишите число, классная работа, тема.

Решение задач с помощью метода вспомогательной площади.

Сегодня, так как это последний урок перед контрольной работой, мы повторим и систематизируем наши знания по теме «Площадь», а также будем решать задачи разными методами в том числе и методом вспомогательной площади.

ІІІ. Актуализация опорных знаний.       

1.     Решение кроссворда.

Дети в полученное поле кроссворда вписывают ответы.

Вопросы:

1) Фигура, с параллельными основаниями.

2) Фигуры, имеющие равные площади.

3) Отрезок, опущенный из вершины геометрической фигуры на её основание или на продолжение основания под прямым углом.

4) Отрезок, соединяющий противолежащие вершины.

5) Отрезок, соединяющий вершину треугольника с серединой противолежащей стороны

6) Фигура, площадь которой можно вычислить при помощи формулы Герона

2.     Проверка результатов.

Какое получилось слово?

Проектируется на экран правильное решение.

3.     Определите какой фигуре соответствует формула площади?

S =

S =

S =

S =

S =

S = h

S =

S =

S =

S =  , где p =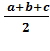

4.     Назовите формулы площади данных фигур

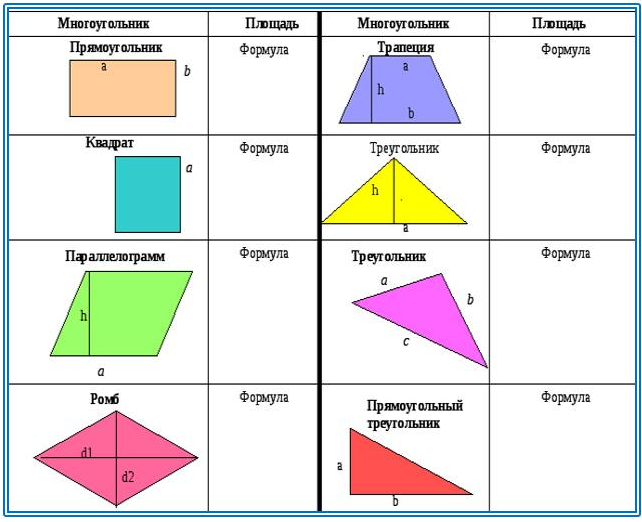
IV. Закрепление знаний и умений.

1.     Повторение свойств площадей.

1)    Медиана треугольника делит его на два треугольника, равных по площади.

2)    Все три медианы треугольника делят его на шесть треугольников, равных по площади.

3)    Если вершину треугольника перемещать по прямой, параллельной противолежащей стороне, то площадь при этом останется прежней

4)    Все три средние линии треугольника делят его на четыре равных треугольника, и, как следствие, равных по площади. Средние линии треугольника площади S отсекают от него треугольники площади S.

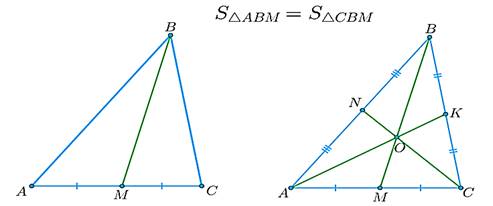
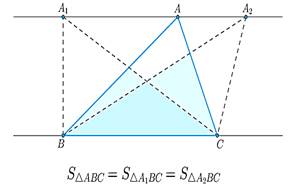
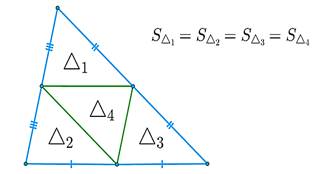
2.     Устное решение задач по готовым чертежам.

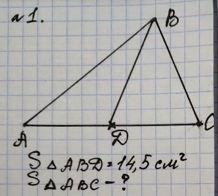
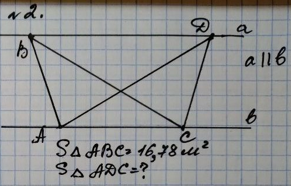
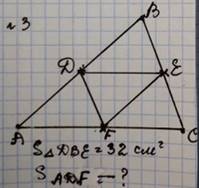
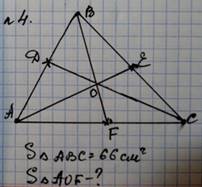
3.     Письменное решение задач у доски.

Трое учащихся работают у доски одновременно или по очереди.

№5. Средняя линия DE треугольника ABC отсекает от него треугольник DBE, площадь которого равна 15 квадратных сантиметров. Найдите площадь трапеции ADEC.

№6. В треугольнике ABC, площадью 120 квадратных метров, О – точка пересечения медиан. Найдите площадь треугольника AОВ.

№7. Вычислить площадь фигуры на клетчатой бумаге любым способом

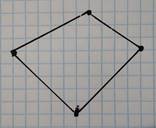
4.     Самостоятельное решение задач практического содержания по вариантам. Обмен работами в парах, взаимопроверка. Проверка по презентации.

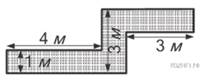
Определите сколько необходимо закупить плёнки (в м²) для гидроизоляции садовой дорожки, изображённой на рисунке, если её ширина везде одинакова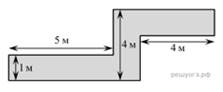

V. Сообщение домашнего д/з, инструктаж.

№1. В треугольнике, площадь которого равнна181,2 м², провели медианы. Получили треугольники трёх видов (разных площадей). Найдите площади треугольников каждого вида (трёх размеров площадей).           

№2. Высота, проведённая из вершины тупого угла прямоугольной трапеции, отсекает квадрат, площадь которого равна 47 см². Найдите площадь трапеции, если её тупой угол равен 135°.                                   

VI. Контроль усвоения материала. Самостоятельная работа на листочках.

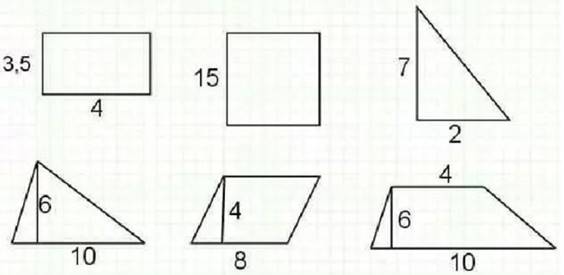
Найдите площадь каждой фигуры и готовые ответы впишите в фигуру на листочке, если нужны вычисления, то считайте в тетради.

1 вариант (прямоугольника, треугольника, трапеции)

2 вариант (квадрата, параллелограмма, прямоугольного треугольника)

VII. Итог урок. Рефлексия.

Я узнал…

Я вспомнил…

Я повторил…        

Мне понравилось…

VIII. Оценивание. 

Резерв.

Верны ли следующие утверждения?

1.     Площади подобных треугольников относятся как коэффициент подобия

2.     Медиана разностороннего треугольника делит его на равные треугольники

3.     Медиана разностороннего треугольника делит его на равновеликие треугольники

4.     Равные фигуры имеют равные площади

5.     Фигуры, имеющие равные площади равны

6.     Средняя линия треугольника отсекает треугольник равный ¼ площади большого треугольника.

7.     Скачано с www.znanio.ru