Урок математики 6 класс Золотое сачение"

Методическая разработка урока математики в 6 классе
Тема «Золотое сечение» учитель математики МиллерЛП
Оборудование:
компьютер, проектор, экран
на партах: карточки с практическими заданиями, измерительная лента, альбом, линейка, калькулятор, простой карандаш, ручка, цветные карандаши, фломастеры или восковые мелки.
Цели:
Математика
• Ознакомить с понятием золотого сечения, его численным значением;
• Формировать вычислительные навыки;
• Прививать интерес к науке и искусству, показать связь математики с искусством.
Изобразительное искусство
1. Ознакомить с каноном изображения человеческой фигуры в искусстве Древнего Египта;
2. Развивать глазомер;
3. Формировать эстетический вкус, развивать творческие способности.
Ход урока:
ЗДРАВСТВУЙТЕ
(слайд 1)Отрывок из стихотворения читает учитель
«Красота есть тайна мира, что в искусстве вновь живёт.
Изгони её из жизни – с ней любовь навек умрёт.
Вздрогнет всё от отвращенья, ночь людей повергнет в страх,
И с последним из поэтов всё погаснет в небесах»
Учитель
(слайд2) Эти строки принадлежат великому немецкому математику, «символу математической строгости» Карлу Вейерштрассу, который считал, что, «математик, который не есть поэт, не будет никогда подлинным математиком».
(слайд3)1. Софьей Ковалевской написаны роман «Нигилистка»,повести «Воспоминание».
(слайд4)2. Н.И.Лобачевский писал стихи.
(слайд5)3. Философ и поэт, классик персидской и таджикской литературы Омар Хайям был известным математиком.
(слайд6)4. Другой пример – математик и логик Чарлз Доджсон. Под псевдонимом Льюис Кэролл он хорошо известен как автор сказки «Приключения Алисы в стране чудес»(слайд7). Как рассказывают биографы, королева Виктория пришла в восторг от этой книги и захотела прочитать всё, написанное Кэрроллом. Можно себе представить её разочарование, когда она увидела на своём столе стопку книг по математике.
(слайд8)На протяжении многих веков пути математики и искусства переплетались.
Сегодня на уроке мы с вами узнаем об одном удивительном открытии математики,которое часто встречается в искусстве и окружающем нас мире. А вот как называется это чудо математики, вы узнаете сами. Откроем тетради, запишем число, классная работа и оставим место для записи темы. Выполним задание.(Давайте вспомним некоторые правила которые нам пригодятся при выполнении задания:
• Как найти дробь от числа
• Как уменьшить число во сколько то раз
• Как увеличить число во сколько то раз
• Как найти процент от числа
А сейчас приступаем к выполнению задания. Каждый учащийся получает карточку выполнять задания начинают с числа, которое стоит в треугольнике, находят это число в круге и выполняют задание , после чего полученное число находят в круге и выполняют задание с этим числом и т. д., выполнив все задания находят число в таблице и выписывают букву соответствующую этому числу. По окончании выполнения задания ребята выходят к доске и открывают букву, соответствующую ответу, если ученик закончил свою работу он может помочь соседу по парте)
|
90 |
28 |
5 |
28 |
2 |
28 |
24 |
|
74 |
24 |
260 |
24 |
52 |
80 |
24 |
После выполнения работы на доске появились слова:
|
З |
О |
Л |
О |
Т |
О |
Е |
|
С |
Е |
Ч |
Е |
Н |
И |
Е |
• (слайд9)Молодцы! Чудо математики называется «Золотое сечение».
• (слайд10)Тема урока, на котором мы рассмотрим неразрывную связь математики и изобразительного искусства, «Золотое сечение».
(слайд11)Что же такое «Золотое сечение»?
(слайд12,13)С давних пор ученые занимались поисками гармонии и совершенства. Одним из таких вопросов был деление отрезка таким образом, чтобы отношение частей было совершенным. Задолго до нашей эры, в различных точках мира, разные ученые, независимо друг от друга,находили это отношение, и у всех это отношение было одним и тем же, а так как отношения были одинаковы, то мы знаем что можно составить пропорцию.
(слайд14)В старших классах , мы аналитически определим значение золотого сечения решив уравнение
Значение золотого сечения принято обозначать Ф(фи) в честь древнегреческого скульптора Фидия, афинского скульптора жившего в V веке до н.э.
Вступительное слово учителя изобразительного искусства:
(слайд15)Рассмотрим пропорциональные величины человеческой фигуры, «божественную пропорцию».
Начнём с искусства Древнего Египта.
В живописи и скульптуре храмов, на предметах домашнего обихода древние египтяне чаще всего изображали богов и фараонов. Были установлены каноны изображения стоящего человека идущего, сидящего. Художники обязаны были заучивать отдельные формы и схемы изображения по таблицам и образцам. Архитекторы Древней Греции совершали специальные путешествия в Египет, чтобы поучиться умению пользоваться каноном.
(слайд16)Перед вами канон изображения стоящего человека, все пропорции человека связаны формулой “золотого сечения”.
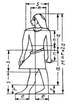 Поэтому
египетские скульпторы могли лепить фигуры больших размеров по частям, т. е.
каждую часть выполняли несколько мастеров порознь, порой даже в разных местах.
Но когда готовые части складывались вместе, то точно сходились без нарушения
пропорций.
Поэтому
египетские скульпторы могли лепить фигуры больших размеров по частям, т. е.
каждую часть выполняли несколько мастеров порознь, порой даже в разных местах.
Но когда готовые части складывались вместе, то точно сходились без нарушения
пропорций.
(слайд 17)Физминутка
Учитель математики:
(слайд18)Отношение большей части отрезка к меньшей и всей длины отрезка к большей его части равно приблизительно 1,618... Обратная величина - отношение меньшей части отрезка к большей и большей части к всему отрезку - составляет примерно 0,618... Эти числа получили название "золотых". Они действительно замечательные. Везде, где человек ощущает гармонию - всюду присутствует "Золотое число".
Учитель изобразительного искусства:
(слайд19)Фидий считал золотое сечение самым гармоничным отношением. В таких работах скульптора, как Зевс Олимпийский, Афина Парфенос, золотое сечение заложено в различных пропорциях человеческого тела. Не только вся статуя, но и отдельные её части делятся в золотом отношении.
 Пропорции “золотого сечения” создают
впечатления гармонии красоты, поэтому скульпторы использовали их в своих
произведениях.
Пропорции “золотого сечения” создают
впечатления гармонии красоты, поэтому скульпторы использовали их в своих
произведениях.
Они же утверждали, что талия делит человеческое тело в отношении “золотого сечения”.
(слайд20)
 Божественную пропорцию» также использовали
зодчие при возведении величественных греческих храмов (Парфенон).
Божественную пропорцию» также использовали
зодчие при возведении величественных греческих храмов (Парфенон).
 Парфенон — главный храм в
древних Афинах, посвященный покровительнице этого города и всей Аттики, богине
Афине.
Парфенон — главный храм в
древних Афинах, посвященный покровительнице этого города и всей Аттики, богине
Афине.
Отношение длины здания Парфенона в Афинах к его высоте равно Ф (фи) т.е 1,618....
Учитель математики:
Выполним практическую работу:
У вас перед глазами два термина золотого сечения:
1.Если разделить любой отрезок на две части так, чтобы отношение целого к большей части отрезка было равно отношению большей части к меньшей, получим сечение, которое называют золотым
![]()
На рисунке отрезок АВ разделен точкой С так, что АВ : АС = АС
: ВС. Если принять длину отрезка АВ за c,
а большую часть отрезка АС за b b CВ
обозначим за а, то с:b
= b:a.
2.термин «Золотое сечение» по Леонардо да Винчи:
"Если
мы человеческую фигуру – самое совершенное творение Вселенной – перевяжем
поясом и отмерим потом расстояние от пояса до ступней, то эта величина будет
относиться к расстоянию от того же пояса до макушки, как весь рост человека к
длине от пояса до ступней”.
(слайд21)
Работая в парах, проверьте термин «Золотое сечение» по
Леонардо да Винчи:
Для
этого необходимо произвести измерения и записать их. Перед тем
как начнем производить измерения необходимо завязать тесьму на самой узкой
части человеческого тела (талии):
а – расстояние от пояса до макушки,
в – расстояние от пояса до ступней,
с – весь рост.
После того как произведены измерения и записаны они надо подставить в пропорцию в = с свои измерения вычислить отношения
а в
вычисления произвести с помощью калькулятора и округлить до разряда десятых,т.е до первой цифры после запятой
Совпадает ли ваше значение с числовым значением золотого числа? (1,618 ....)
(слайд22)интересные факты
Учитель изобразительного искусства:
(слайд23)Предлагаю нарисовать древнегреческую амфору по правилам «золотого сечения»:
Особым
видом изобразительного искусства Древней Греции считается изготовление и
роспись ваз. В
изящной форме
легко угадываются пропорции золотого сечения .
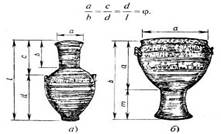
Сначала выполняем геометрические построения: вертикально строим отрезок длиной, соответствующей высоте амфоры, и делим его в отношении, равном золотому сечению (8:5). Теперь рисуем амфору: (Учитель показывает на доске, учащиеся выполняют на альбомных листах. Если позволяет время, можно раскрасить вазу или нанести орнамент).
(слайд24)Итог урока:
Мы наглядно убедились, что в мире царит всеобщая закономерность, а сущность прекрасного заключается в строгом порядке, гармонии частей и целого, в правильных математических отношениях. Математика не только царица наук, но и основа искусств.
(слайд25)Домашнее задание
• Проверить термин «Золотое сечение» по Леонардо да Винчи на фигуре своей мамы, папы, брата или сестры.
• Дорисовать древнегреческую амфору.
слайд26)Рефлексия
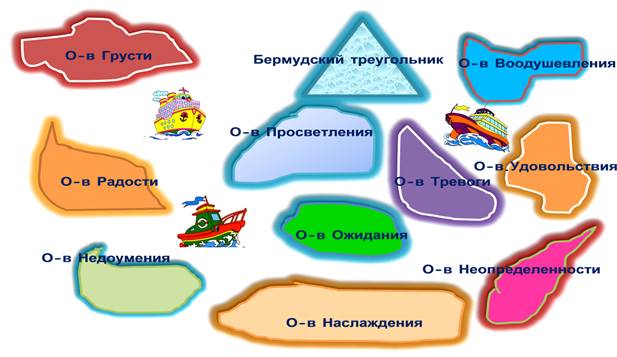
(слайд27) Перед вами карта с изображением эмоциональных "островов": о. Радости, о. Грусти, о. Недоумения, о. Тревоги, о. Ожидания, о. Просветления, о. Воодушевления, о. Удовольствия, о. Наслаждения.
Вы обсудив в группе и по одному человеку от группы выходя к карте крепят свой стикер в соответствующем районе карты, который отражает душевное, эмоционально-чувственное состояние после урока.
Литература
1. Журнал «Математика в школе» №3 2001 г., статьи «Присутствие красоты» Е. И.
2. Чепраковой, «О золотом сечении и не только о нём» А. А. Ятайкиной, «Математика как изящное искусство и её роль в общем образовании» Я. Шатуновского.
3. К. Вёрман «История искусства» в 2-х частях, М.: «Издательство АСТ», 2000 г.
4. Энциклопедический словарь юного математика. М., 1989.
5. Энциклопедический словарь юного художника. Составители: Н.И.Платонова, В.Д. Синюков. М.: «Педагогика», 1983.
© ООО «Знанио»
С вами с 2009 года.
![]()

