Урок математики в 5 классе "Сложение и вычитание обыкновенных дробей"

Конспект урока  по теме

«Сложение и вычитание обыкновенных дробей».

Цель: Закрепить навык решения примеров и задач на сложение и вычитание обыкновенных дробей и смешанных чисел.

Задачи:

• Образовательная: Продолжить закрепление навыков решения примеров и задач на сложение и вычитание обыкновенных дробей и смешанных чисел, закрепить вычислительные навыки.
• Развивающая: Развивать логическое мышление учащихся, интерес к математике, навыки самостоятельной работы, а так же навыки самопроверки выполненного.
• Воспитательная: Воспитывать математическую культуру, уважение мнения одноклассников, умение слушать, организованность, ответственность.

Ход урока:

1. Организационный момент.

Приветствие. Постановка темы и целей урока.

2. Фронтальный опрос.

Задание: продолжи предложение.

1)    При сложении дробей с одинаковыми знаменателями… (…знаменатель остается тем же, а числители складываются)

2)    Чтобы вычесть дроби с разными знаменателями, надо… (…привести их к наименьшему общему знаменателю и выполнить вычитание дробей с одинаковыми знаменателями)

3)    Если знаменатели дробей – взаимно простые числа, то наименьшим общим знаменателем будет… (…произведение этих дробей)

4)    Если один из знаменателей делится на другой, то наименьшим общим знаменателем будет… (…больший знаменатель)

5)    При сложении дроби с целым числом получается… (…смешанное число)

6)    При сложении целого числа и смешанного получается… (…смешанное число)

7)    Чтобы сложить смешанные числа, надо… (…сложить их целые части и прибавить сумму дробных частей)

8)    Чтобы сложить дробь и смешанное число, надо… (…к дроби прибавить дробную часть смешанного числа, а затем прибавить целую часть смешанного числа)

9)    Если при сложении дробей получается неправильная дробь, то надо… (…результат записать в виде смешанного числа)

10)                       Чтобы из единицы вычесть дробь, надо… (…единицу записать в виде дроби со знаменателем, равным знаменателю дроби, которую вычитаем)

3. Устный счет.

Задание: найдите значение выражения:

1)   . Ответ:

2)   . Ответ:

3)  . Ответ:

4)   . Ответ:

5)   . Ответ: 4

6)  . Ответ:

7)   . Ответ:

8)   . Ответ:

9)   . Ответ:

10)                       Помоги правильно расставить знаки в следующем выражении: 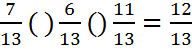. Ответ: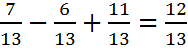

11)                       Раньше в Древнем Египте вместо знаков «+» и «-» использовались знаки «»  и «»  («идущие ноги»). Отгадайте, какой из знаков обозначает сложение, какой вычитание.

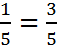
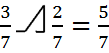
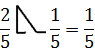
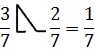
Ответ: «» = «+», «» = «-»

4. Закрепление.

Открываем учебники, выполним № 671.

Выполняем у доски 1 и 2 примеры:

1) 

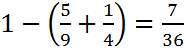
2) 

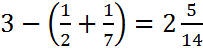
5. Самостоятельная работа с последующей проверкой.

Остальные примеры выполняем самостоятельно:

1 ряд выполняет 3 пример,

2 ряд выполняет 4 пример,

3 ряд выполняет 5 пример.

3) 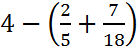 . Ответ: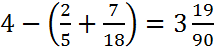

4) 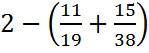 . Ответ:

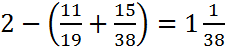
5) 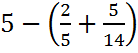 . Ответ:

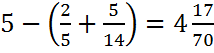
6. Устная работа.

Я читаю утверждения, если вы с ними согласны, то хлопаем в ладоши.

1)    Дробь три четвертых – правильная дробь. (да)

2)    Дробь четыре двенадцатых – несократимая дробь. (нет)

3)    Дробь тринадцать четырнадцатых – несократимая дробь. (да)

4)    Дробь пять седьмых – правильная дробь. (да)

5)    Дробь три десятых – сократимая дробь. (нет)

6)    Дробь шесть пятых – правильная дробь. (нет)

7)    Дробь десять пятнадцатых – сократимая дробь. (да)

8)    Дробь десять двенадцатых – несократимая дробь. (нет)

9)    Дробь две пятых – правильная дробь. (да)

Хорошо! Продолжаем работать.

7. Закрепление.

Выполним следующую задачу:

Одна сторона треугольника равна  м, вторая его сторона короче первой на  м. Если периметр треугольника  м, то сколько метров составляет его третья сторона? ()

Ответьте на вопросы:

Что известно в задаче?

Что неизвестно?

Как найти неизвестное?

Задачу разобрали, приступаем к решению.

8. Работа по карточкам.

Пока мы будем решать задачу, несколько учеников выполнят работу по карточкам. (8 карточек)

9. Закрепление.

Решить уравнение:

. Ответ:

10. Дома решите уравнения № 720

1)

2)

3)

4)

11. Самостоятельная работа.

Решите уравнения:

12. Итог урока.

Повторили правила сложения и вычитания обыкновенных дробей.

Применяли данные правила при решении примеров, уравнений и задачи.