
Тема урока: «Решение задач с помощью квадратных уравнений»
1.Сообщение темы и цели урока.
Вспомним, что мы изучили на предыдущих уроках алгебры? Какую тему? Чему научились?
(Ответы: Квадратные уравнения, научились их решать)
Зачем нам нужно уметь решать квадратные уравнения? В чем нам эти знания могут пригодиться?
(Ответ: при решении задач)
Как вы думаете, какой же будет тема сегодняшнего урока?
(Ответ: «Решение задач с помощью квадратных уравнений»).
Запишите сегодняшнее число и тему урока в тетради!
И так, тема нашего урока «Решение задач с помощью квадратных уравнений». Всякая хорошо решеная математическая задача доставляет умственное наслаждение. Эти слова Г. Гессе станут эпиграфом нашего урока. Надеюсь, что вы действительно получите удовольствие от результатов вашего труда на уроке.
2.Повторение и закрепление пройденного материала.
Сначала проверим, как вы усвоили пройденный материал.
Фронтальный опрос.
Какие уравнения называются квадратными?
Сколько корней имеет квадратное уравнение, если D>0?
Сколько корней имеет квадратное уравнение, если D=0?
Сколько корней имеет квадратное уравнение, если D<0?
Как называется квадратное уравнение, где хотя бы один их коэффициентов b или с равен нулю?
Какие уравнения называются приведенными квадратными?
Можно ли неприведенное квадратное уравнение представить в виде приведенного?
Каким образом?
МОЛОДЦЫ!!! Вы успешно прошли блиц-опрос.
Тест « Виды квадратных уравнений»
|
Ф.И. |
полное |
неполное |
приведённое |
неприведённое |
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
|
|
|
3𝑥+6 |
|
|
|
|
Ребята выполняют работу, а затем меняются листочками и по ключу проверяют ответы, оценивая работу товарища. Результат записывается в «Карту результативности» -колонка «Тест».
Ключ к тесту:
|
1. |
+ |
|
+ |
|
|
2. |
|
+ |
|
+ |
|
3. |
|
+ |
+ |
|
|
4. |
+ |
|
|
+ |
|
5. |
+ |
|
|
+ |
б) Провоцирующая задача
Чему равно: 2 в квадрате? 3 в квадрате? 5 в квадрате? Угол в квадрате? ( в квадрате все углы прямые).
3. Контроль усвоения материала (письменный опрос с последующей взаимопроверкой).
|
Уравнение |
а |
в |
с |
в2-4ас |
х1 |
х2 |
|
х2-6х+9=0 |
|
|
|
|
|
|
|
2x2+7x+9=0
|
|
|
|
|
|
|
Вариант 1.
1) Напишите формулу корней квадратного уравнения ах2+вх+с=0.
2) Заполните таблицу:
|
Уравнение |
а |
в |
с |
в2-4ас |
х1 |
х2 |
|
x2-8x+16=0
|
|
|
|
|
|
|
|
2x2-3x+5=0
|
|
|
|
|
|
|
Вариант 2.
1) Напишите формулу корней квадратного уравнения ах2+вх+с=0
2) Заполните таблицу:
Задание: Составьте квадратное уравнение, используя следующие данные:
А) Многие, уходя из
кабинета, не выключают свет. Да и дома порой зажигают все лапы, когда в этом
нет необходимости. Кто-то может сказать: мелочь! Между тем сосчитайте, сколько
за 10 часов расходует одна лампочка в 100 Вт. Ответ переведите в кВт. Полученное
число будет первым коэффициентом квадратного уравнения. Ответ: ![]() Вт =1кВт, а =1.
Вт =1кВт, а =1.
Б) А что такое капля воды из неплотно закрытого крана? За час теряется 0,6л, а за сутки – .. ? (14,4л воды). В данном числе сложите цифры. Полученное число будет вторым коэффициентом. Ответ: 14.4л, 1+4+4 = 9, в=9.
В) К обеду школа получает
35 кг хлеба, в бачках для отходов остаётся ![]() часть этого хлеба. Труд скольких людей пропадает
зря! Посчитайте сколько хлеба выбрасывается ежедневно и удвойте это число.
Полученное число будет третьим коэффициентом.
часть этого хлеба. Труд скольких людей пропадает
зря! Посчитайте сколько хлеба выбрасывается ежедневно и удвойте это число.
Полученное число будет третьим коэффициентом.
Ответ: ![]() ,
, ![]() , с=14.
, с=14.
Г) Все коэффициенты
положительные числа. Составьте квадратное уравнение, решите его. Ответ: у2+9у+14=0;
D=25, у1,2= ![]() ; у1 = -7,у2 =
-2.
; у1 = -7,у2 =
-2.
3.Изучение нового материала.
Ребята! Есть проблема. Я
надеюсь, вы мне поможете. Мне необходимо обнести забором cадовый участок, он
имеет прямоугольную форму. Одна из сторон на 10 метров больше другой, площадь
всего участка 1200![]() . Сколько необходимо мне
закупить материала? Возможно ли, решить задачу с помощью квадратного уравнения?
. Сколько необходимо мне
закупить материала? Возможно ли, решить задачу с помощью квадратного уравнения?
Решение задачи:
Выбираем наименьшую из сторон,
обозначаем ее – х метров. Тогда большая сторона (х+10) метров. Знаем, что
площадь всего участка 1200![]() . Получаем уравнение:
. Получаем уравнение:
х(х+10)=1200,
Раскроем скобки.
![]() +10х=1200,
+10х=1200,
![]() +10х-1200=0,
+10х-1200=0,
D=100+4800=4900,
![]() =
=![]() =-40,
=-40, ![]() =
=![]() =30.
=30.
Корень уравнения равный
-40 –не подходит, так как длина не может быть отрицательной величиной; ![]() =30 м – это длина
наименьшей стороны изгороди. Значит х+30=40 м – наибольшая сторона изгороди, а
длина всей изгороди, т.е. периметр участка, будет равен Р=2×(30+40)=140
метров. Следовательно, мне необходимо купить 140 метров материала для
обнесения огородного участка изгородью.
=30 м – это длина
наименьшей стороны изгороди. Значит х+30=40 м – наибольшая сторона изгороди, а
длина всей изгороди, т.е. периметр участка, будет равен Р=2×(30+40)=140
метров. Следовательно, мне необходимо купить 140 метров материала для
обнесения огородного участка изгородью.
Ответ: 140 м.
С чего же нужно начинать решать задачи? Отвечают дети с помощью учителя.
1.Выбрать неизвестную величину.
2.Затем составить уравнение.
3.Решить его.
4. Сделать вывод о корнях.
5. Выполнить дополнительные действия.
5. Этап самостоятельного применения знаний в сходной и новой ситуациях
Составить уравнения к задачам, при этом корни уравнения находить не надо (7-10 минут).
1. Найти два последовательных натуральных числа, произведение которых равно 210.
2. Площадь прямоугольника, одна из сторон которого на 3 см больше другой, равна 54 см². Найти стороны и периметр прямоугольника.
По окончании времени учащиеся выходят к доске и записывают полученные уравнения с комментариями.
Ответы:
1. х(х + 1) = 210; х2 + х ─ 210 = 0
2. х(х + 3) = 54; х2 +3х ─ 54 = 0
На шахматном турнире каждый сыграл с соперником по 1 партии. Всего было сыграно 45 партий. Сколько участников было на турнире?
Решение
Пусть участников было x. Тогда каждый сыграл x(x-1) партию. Казалось бы, приравняли к 45, решаем… А целого ответа нет. Почему так? Да потому, что мы каждую партию посчитали дважды (например, партия Вася – Петя и Петя – Вася посчитаны как разные партии, но ведь это одна и та же партия). Значит, количество партий x(x-1)/2 . Тогда получаем: x(x-1)/2=45.
X2-x-90=0
-9,10
Ответ 10
Задача по физике.
Мяч брошен вертикально вверх с начальной скоростью 40 м/с. Через сколько секунд оно окажется на высоте 60 м?
Решение. Из курса физики
известно, что если не учитывать сопротивление воздуха, то высота h(м), на
которой брошенный вертикально вверх мяч окажется через t(c), может быть найдена
по формуле ![]() , где
Vo(м/с)-начальная скорость, g-ускорение свободного падения, приближенно равное
10 м/с2. Подставив значения h и V в формулу, получим 60=40t-5t2. Получили
квадратное уравнение, решим его. 5t2-40t+60=0, t2-8t+12=0, D=16, t1=2; t2=6.
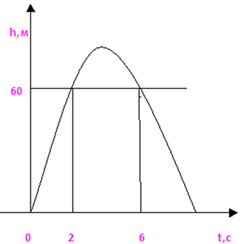
Рассмотрим график зависимости h от t, где h=40t-5t2. Из графика видно, что мяч,
брошенный вертикально вверх, в течении первых 4с поднимается вверх до высоты 80
м, а затем начинает падать. На высоте 60 м от земли оно оказывается дважды:
через 2 с и через 6 с после бросания. Условию задачи удовлетворяют оба
найденных корня.
, где
Vo(м/с)-начальная скорость, g-ускорение свободного падения, приближенно равное
10 м/с2. Подставив значения h и V в формулу, получим 60=40t-5t2. Получили
квадратное уравнение, решим его. 5t2-40t+60=0, t2-8t+12=0, D=16, t1=2; t2=6.
Рассмотрим график зависимости h от t, где h=40t-5t2. Из графика видно, что мяч,
брошенный вертикально вверх, в течении первых 4с поднимается вверх до высоты 80
м, а затем начинает падать. На высоте 60 м от земли оно оказывается дважды:
через 2 с и через 6 с после бросания. Условию задачи удовлетворяют оба
найденных корня.
Ответ: на высоте 60 м тело окажется через 2 с и через 6 с.
6. Этап подведения итогов урока и информации о домашнем задании
а) Дать качественную оценку работы класса и отдельных учащихся.
Сегодня на уроке мы ещё раз убедились зачем нужно решать квадратные уравнения. С помощью квадратных уравнений решаются задачи из различных сфер деятельности: в геометрии, в физике, на шахматных турнирах. Задачи на квадратные уравнения впервые встречается в работах индийских учёных в 499 году. В Древней Индии были распространены публичные соревнования в решении трудных задач. Задачи часто облекались в стихотворную форму. Например:
б) Задание на дом.
Задача Бхаскары (знаменитый индийский математик XII века):
Решить задачу: «Обезьянок резвых стая,
Всласть поевши, развлекалась.
Их в квадрате часть восьмая,
На поляне забавлялась.
А двенадцать по лианам
Стали прыгать, повисая.
Сколько ж было обезьянок,
Ты скажи мне, в этой стае?»
(Очень эмоциональным и логически завершающим урок моментом может послужить литературная страничка. Математику относят к точным наукам, где нет места лирике. Однако очень важно показать ребятам, что это далеко не так. Рассказывайте им, что среди математиков всегда было и есть много поэтов, стремящихся показать красоту этой древней науки в стихах.)
Решите уравнения:
1. х2 − 5х + 6 = 0 (Ответ: 2; 3)
2. 6у2 − 5у + 1 = 0 (Ответ: 1/3; 1/2)
Сравните в этих уравнениях коэффициенты, свободные члены и корни между собой. Какая наблюдается закономерность между ними? Какую гипотезу можно выдвинуть для таких уравнений? Составите несколько пар уравнений такого вида
(Ученикам предлагается, в качестве творческой домашней работы, составить несколько пар уравнений такого вида, исследовать их и доказать выдвинутое предположение в общем виде.)
8. Рефлексия: продолжи мысль:
Сегодня я выполнял задания…
Сегодня я понял, что…
Было трудно…
Я попробую…
Урок дал мне для жизни…

Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.