Урок_1_Решение текстовых задач_Методические рекомендации

Методические рекомендации к уроку №1

темы/подраздела «Квадратичная функция и ее график »

раздела «Квадратичная функция»

Тема урока: Решение текстовых задач

Цель обучения:

8.4.2.3 использовать квадратичную функцию для решения прикладных задач;

8.4.3.1 составлять математическую модель по условию задачи

Учащиеся будут рассматривать задачи на применение квадратичной функции в разнообразных ситуациях.

Методические рекомендации по организации урока. Рекомендации по формативному оцениванию

В начале урока учащимся предлагается упражнение, цель которого – создание положительного настроя и благоприятного климата в классе.

Для рассмотрения темы урока предлагается задача, контекст которой позволяет рассмотреть применение квадратичной функции при строительстве мостов. Исследовательская работа позволит учащимся рассмотреть еще один пример, когда квадратичная функция используется для описания реальных процессов, в данном случае – траектории полета мяча. Учащиеся будут выполнять измерения и расчеты, чтобы выстроить эту траекторию, это позволит развивать функциональную грамотность учащихся.

Решение текстовых задач в парах или группах поможет создать возможности для взаимообучения и взаимооценивания. В соответствии с планом урока каждая пара учащихся выступит в роли оцениваемых и оценивающих. К данному времени учащиеся должны хорошо владеть математическими терминами по данной теме. Чтобы процесс взаимооценивания продвигался быстрее, можно провести оценивание по рядам. Когда учитель выслушает по одной паре учащихся для каждой задачи, учащиеся могут далее оценивать друг друга по цепочке. А учитель может передвигаться по классной комнате, слушать как проходит процесс обсуждения задач, следить за корректностью использования математического языка, оказывать при необходимости поддержку учащимся.

Дополнительные разноуровневые задания

Уровень В

1.   График функции  проходит через точки А(0; 2), В(2; 0), С(3; 8). Найдите значения коэффициентов a, b, c.

2.   При каком значении параметра k график функции :

а) пересекает ось абсцисс в двух точках;

б) касается оси абсцисс;

в) не имеет общих точек с осью абсцисс?

Уровень С

Постройте графики функций,  укажите область определения, множество значений, промежутки возрастания и убывания.

1.        

2.        

Ответы и решения

Задание 2.

Связь между шкалами градусов Цельсия и градусов Фаренгейта  находится по формуле T_F=32+1,8· T_c 

Заполнить таблицу:

Группа В

Задание 1.

Футболист подбросил мяч вверх. Высота над землей подброшенного вверх мяча меняется по закону .  Через сколько секунд мяч упадет на землю?

Решение.

Ответ: через 3 с.

Задание 2.

Один из способов измерения глубины пещер, колодцев, шахт и т.д. заключается в следующем. Сверху сбрасывают камень и с максимально возможной точностью засекают время, через которое будет услышан звук от его удара о землю. Заполните таблицу, если закон свободно падающего тела вычисляется по формуле, g≈10 м/с² (9,8 м/с²)

Группа С

Задание 2.

После начала торможения движение электропоезда описывается законом , а скорость меняется по закону V=16-0,2t, где t - время (с), v - скорость (м/с), S - пройденный путь (м). Через сколько секунд поезд остановится? Каков его тормозной путь? Постройте графики этих функций S=S(t), v=v(t).

Решение.

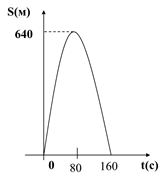
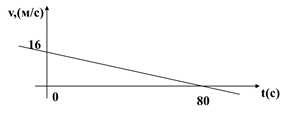
Поезд остановится через 80 с.

=640

Тормозной путь составляет 640 м.

Список полезных ссылок и литературы

1. Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Феоктистов И.Е. Алгебра. 9 класс : учеб. для учащихся общеобразоват. учреждений.  – М.: Мнемозина, 2010

2. Галицкий М.Л., Гольдман А.М., Звавич Л.И. Сборник задач по алгебре, 8-9 классы.  – М.: Просвещение, 2009. 301 с.: ил.