Урок_1_Решение текстовых задач_План урока

Краткосрочный план

Раздел 8.3А: Квадратичная функция

Школа:

Дата:

ФИО учителя:

Класс: 8

Количество присутствующих:

Количество отсутствующих:

Тема урока

Решение текстовых задач

Урок №1 серии из 6 уроков

Тип урока

Изучение нового материала

Цели обучения (ссылка на учебную программу)

8.4.2.3

использовать квадратичную функцию для решения прикладных задач;

8.4.3.1

составлять математическую модель по условию задачи

Цели урока

Использовать график и свойства квадратичной функции для решения задач

Критерии оценивания

Языковые цели

Учащиеся объясняют, как использовать свойства или график квадратичной функции в конкретной ситуации.

Предметная лексика и терминология

− квадратичная функция

− функция

− значение функции

− аргумент

− значение аргумента

− наибольшее / наименьшее значение

Серия полезных фраз для диалога/письма

Наибольшее / наименьшее значение функция достигает в вершине параболы

Привитие ценностей

Функциональная грамотность - умение применять полученные знания и навыки для личных, социальных, экономических целей.

Осуществляется через содержание урока.

Межпредметные связи

Решение задач с физическим, географическим контекстом.

Навыки использования ИКТ

Презентация

Предварительные знания

Учащиеся знают свойства квадратичной функции, умеют определять их по графику квадратичной функции.

Ход урока

Этапы урока

Запланированная деятельность на уроке

Ресурсы

Начало урока

2мин

Организационный момент

Учащиеся делятся на группы по 5-6 человек, каждая группа становится в круг. Вытянув правую руку в центр, учащиеся говорят одно пожелание соседу слева.

Учитель объявляет тему урока и цели обучения, объясняет, что квадратичная функция имеет широкое применение при решении практических задач. Примеры таких задач будут рассмотрены на протяжении последующих нескольких уроков.

Презентация

Слайды 1-3

Середина урока

10 мин

15 мин

Введение в тему урока

Учащиеся, работая в группах, будут решать задачи на применение свойств квадратичной функции. Сначала обсуждение проходит в группе, затем решение будет рассмотрено у доски.

Задание:

Используя формулу , запишите функцию описывающую мост «Павлодар-Ақсу».

Данные:

Центральная часть мостового перехода представлена неразрезным металлическим пролётным строением по схеме 110,5+252+110,5 м с высотой центральной арки 40 ми представляет собой 3-х пролётную неразрезную арку с ездой понизу с системой гибких перекрестных подвесок. Общая протяженность мостового перехода составляет 12,3 км. Центральная часть мостового перехода - уникальное архитектурное сооружение. Центральная арка мостового перехода длиной 252 метра - самая большая в Центральной Азии.

Решение:

График функция проходит через точку.

Учащиеся делают вывод, что квадратичная функция используется при построении мостов:

Почему при построениие мостов используются параболы? Учащиеся приводят свои аргументы. (Учитель поясняет с технической точки зрения).

Исследовательская работа в группах

Каждой группе учащихся предлагается рисунок с остановленным кадром броска мяча в корзину. Требуется определить попадет ли мяч в корзину, если известно, что траектория полета мяча, брошенного под углом к горизонту, является частью параболы. Учащиеся анализируют как лучше всего расположить координатную плоскость для решение поставленной задачи.

Рисунок для группы 1

Рисунок для группы 2

Рисунок для группы 3

Рисунок для группы 4

После окончания работы группы обмениваются работами, проводят взаимооценивание, используя дескрипторы.

Дескрипторы

1.                  Правильно построена координатная плоскость;

2.                  Правильно определена вершина параболы;

3.                  Правильно построена парабола;

4.                  Сделан вывод.

Обратная связь:

Что было достигнуто?

На каком этапе задания Вы чуствовали себя уверенно?

Что нужно улучшить?

Гимнастика для глаз

Индивидуальная работа

Учащиеся выполняют задания, учитель обходит класс, проверяет работы учащихся.

Группа А

Задание 1. Если на дне железной консервной банкипробить отверстие и налить в нее воду, то уровень воды будет убывать по закон .

Постройте график функции.

Задание 2.

Связь между шкалами градусов Цельсия и градусов Фаренгейта  находится по формуле T_F=32+1,8· T_c

Заполнить таблицу:

Группа В

Задание 1.

Футболист подбросил мяч вверх. Высота над землей подброшенного вверх мяча меняется по закону .  Через сколько секунд мяч упадет на землю?

Задание 2.

Один из способов измерения глубины пещер, колодцев, шахт и т.д. заключается в следующем. Сверху сбрасывают камень и с максимально возможной точностью засекают время, через которое будет услышан звук от его удара о землю. Заполните таблицу, если закон свободно падающего тела вычисляется по формуле, g≈10 м/с² (9,8 м/с²)

Группа С

Задание 1.

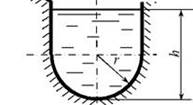
Скорость  течения  в  канале  на  различных  глубинах  выражается  формулой,
где   —  глубина  слоя  (в  метрах),   —  скорость  (в  м/мин).  Исследуйте,  как  меняется  с  глубиной  погружения  скорость  движения  воды.  На  какой  глубине  скорость  течения  наибольшая? Исследуйте  изменение скорости взависимости от глубины канала.

Задание 2.

После начала торможения движение электропоезда описывается законом , а скорость меняется по закону V=16-0,2t, где t - время (с), v - скорость (м/с), S - пройденный путь (м). Через сколько секунд поезд остановится? Каков его тормозной путь? Постройте графики этих функций S=S(t), v=v(t).

Учащиеся выполняют взаимопроверку, далее фронтальное обсуждение решения по слайдам.

Дескрипторы:

1.                  Правильно определяет три этапа математического моделирования;

2.                  Правильно использует алгебраические выражения и формулы по условию задачи;

3.                  Правильно преобразует математическую модель;

4.                  Правильно найден ответ.

Слайд 4

Приложение 1

Слайд 5

Слайд 6

Конец урока

3 мин

2 мин

Рефлексия

- Какие задания и виды деятельности были интересными?

- Что было трудным? Почему?

Домашнее задание

1. С башни выпустили вверх стрелу из лука. Если начальная скорость стрелы равна 50 м/с, высота башни 20 м и t – время полёта стрелы (в секундах), то расстояние h (в метрах) стрелы от поверхности земли можно найти по формуле h=-5t²+50t+20.

Какой наибольшей высоты достигнет стрела?

Постройте график движения стрелы по уравнению h= -5t² +50t+20.

На графике отметьте точку, в которой стрела достигнет наибольшей высоты.

2. Решите задачу составлением уравнения:

Из двух городов, расстояния между которыми 500 км одновременно вышли навстречу друг другу трактор и грузовик. Если скорость грузовика в 4 раза больше скорости трактора и они встретились через 4 часа, то чему равна скорость трактора?

Слайд 7

Дифференциация – каким образом Вы планируете оказать больше поддержки? Какие задачи Вы планируете поставить перед более способными учащимися?

Оценивание – как Вы планируете проверить уровень усвоения материала учащимися?

Здоровье и соблюдение техники безопасности

Учащиеся будут работать в парах, чтобы иметь возможность для поддержки более сильными учениками.

Учащиеся будут оценивать друг друга во время решения задач.

Учитель будет обходить класс, предоставляя устные комментарии.

Учащиеся будут менять виды деятельности для поддержания концентрации внимания и работоспособности.

Рефлексия по уроку

Были ли цели урока/цели обучения реалистичными?

Все ли учащиеся достигли ЦО?

Если нет, то почему?

Правильно ли проведена дифференциация на уроке?

Выдержаны ли были временные этапы урока?

Какие отступления были от плана урока и почему?

Используйте данный раздел для размышлений об уроке. Ответьте на самые важные вопросы о Вашем уроке из левой колонки.

Общая оценка

Какие два аспекта урока прошли хорошо (подумайте как о преподавании, так и об обучении)?

1:

2:

Что могло бы способствовать улучшению урока (подумайте как о преподавании, так и об обучении)?

1:

2:

Что я выявил(а) за время урока о классе или достижениях/трудностях отдельных учеников, на что необходимо обратить внимание на последующих уроках?