
 1)
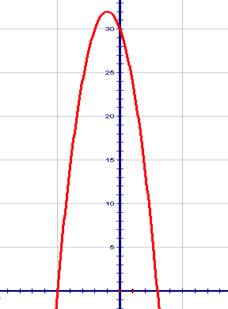
Составьте уравнение параболы
1)
Составьте уравнение параболы ![]() , которая пересекает ось
, которая пересекает ось
![]() в точках
в точках ![]() , а ось
, а ось ![]() –
в точке
–
в точке ![]() .
.
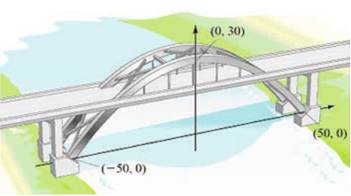
2) Для поддержки моста нужно создать металлическую конструкцию параболической формы, которая должна проходить через точки (-50, 0), (0, 30) и (50, 0). Напишите уравнение параболы, образованной мостом
3) Футболист на тренировке
подбросил мяч вертикально вверх. Высота (h), на
которой находится мяч через t секунд полета вычисляется по формуле ![]() , где g
≈ 10 (м/с2). Через сколько секунд мяч упадет на землю?
, где g
≈ 10 (м/с2). Через сколько секунд мяч упадет на землю?
4)
Река протекает по лугу, образуя кривую ![]() (единица длины – 1 км). Прямолинейное
шоссе проходит вдоль оси ОХ и дважды пересекает реку. Определите расстояние
между мостами, проложенными через реку.
(единица длины – 1 км). Прямолинейное
шоссе проходит вдоль оси ОХ и дважды пересекает реку. Определите расстояние
между мостами, проложенными через реку.
Дополнительное задание
Парабола
задана уравнением ![]() . Справедливы ли
следующие утверждения?
. Справедливы ли
следующие утверждения?
1)
Если уравнение у = 0 имеет два корня, то ![]() .
.
2) Если один из корней уравнения у = 0 равен 2, то b = –2,5.
3) Если b < –2, то вершина параболы лежит в четвертой четверти.
4)
Если b > 0, то функция ![]() возрастает при x
> –1.
возрастает при x
> –1.
Домашнее задание
1) С двухметровой высоты под углом
к горизонту выпущена сигнальная ракета. Изменение высоты её полёта h (м) в зависимости
от времени движения t (c) описывается
формулой ![]() .
Постройте график данной функции.
.
Постройте график данной функции.
Используя график, ответьте на вопросы:
а) В какое время ракета поднимется на высоту 20 м и в какое время она окажется на той же высоте при спуске?
б) На какой высоте ракета будет через 3,5 с полёта?
в) Укажите наибольшую высоту подъёма ракеты. Сколько времени потребовалось ракете, чтобы подняться на максимальную высоту?
2) Вычислите: ![]() .
.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.