Урок_2_Решение текстовых задач_Методические рекомендации (1)

Методические рекомендации к уроку №2

темы/подраздела « Квадратичная функция и ее график »

раздела « Квадратичная функция»

Тема урока: Решение текстовых задач

Цель обучения:

8.4.2.3 использовать квадратичную функцию для решения прикладных задач;

8.4.3.1 составлять математическую модель по условию задачи.

Учащиеся рассмотрят решение прикладных задач с помощью составления и исследования математической модели в виде квадратичной функции.

Методические рекомендации по организации урока. Рекомендации по формативному оцениванию

В начале урока учащимся предлагается задание на определение свойств квадратичной функции. Учащиеся должны записывать свойства на мини-досках. На слайдах будут продемонстрированы верные ответы, чтобы учащиеся могли сразу оценить свое понимание материала.

Также во время устной работы учащимся будет предложено нестандартное задание.

Письменная работа начинается с совместного разбора задания на составление уравнения функции. Затем учащиеся развивают этот навык при решении задачи о мосте. Здесь предлагается организовать работу в парах. Но учитель может изменить ход урока.

Дополнительные задания направлены на развитие критического мышления учащихся. Если в течение урока будет недостаточно времени для их решения, то можно предложить их в качестве домашнего задания по крайней мере сильным учащимся вместо №2 на вычисление значения выражения.

Ответы и решения

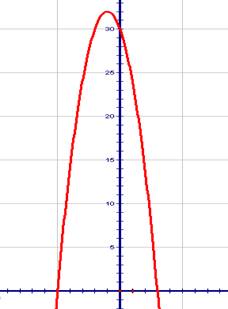1) Составьте уравнение параболы   , которая пересекает ось   в точках   , а ось   – в точке  .     

Решение.

Квадратичная функция, задающая эту параболу, будет иметь вид   .  Точка пересечения с осью  имеет абсциссу . При  значение функции должно равняться . Получаем:

Ответ:

2) Для поддержки моста нужно создать металлическую конструкцию параболической формы, которая должна проходить через точки (-50, 0), (0, 30) и (50, 0). Напишите уравнение параболы, образованной мостом

.

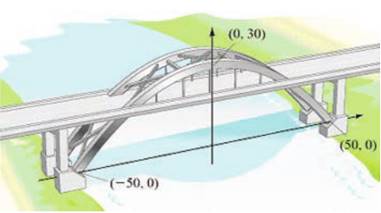
Решение.

Пусть . Поскольку точки (-50, 0), (0, 30) и (50, 0) принадлежат графику функции, то координаты этих точек удовлетворяют уравнению параболы:

;

;

.

Отсюда, ; , уравнение параболы имеет вид .

Ответ: .

3) Футболист на тренировке подбросил мяч вертикально вверх. Высота (h), на которой находится мяч через t секунд полета вычисляется по формуле , где g ≈ 10 (м/с²). Через сколько секунд мяч упадет на землю?

Решение.

t = 0, t = 3.

Ответ: Через 3 с.

4) Река протекает по лугу, образуя кривую  (единица длины – 1 км). Прямолинейное шоссе проходит вдоль оси ОХ и дважды пересекает реку. Определите расстояние между мостами, проложенными через реку.

Решение.

Найдем нули функции:

Полученный результат означает, что точки пересечения реки и шоссе имеют координаты (0; 0) и (5; 0), следовательно искомое расстояние составляет 5 км.

Ответ: 5 км.

Дополнительные разноуровневые задания

Уровень В – вопросы 1 и 2.

Уровень С – вопросы 3 и 4.

Парабола задана уравнением . Справедливы ли следующие утверждения?

1) Если уравнение у = 0 имеет два корня, то .

2) Если один из корней уравнения у = 0 равен 2, то b = –2,5.

3) Если b < –2, то вершина параболы лежит в четвертой четверти.

4) Если b > 0, то функция  возрастает при x > –1.

Ответ: 1) да; 2) да; 3) да; 4) нет.

Список полезных ссылок и литературы

1. Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Феоктистов И.Е. Алгебра. 9 класс : учеб. для учащихся общеобразоват. учреждений.  – М.: Мнемозина, 2010

2.  «Кенгуру» - выпускникам 9 класса. Тест готовности к продолжению образования.

3. Курбанов К.О. Некоторые прикладные задачи по высшей математике (методическое пособие). – Махачкала: Махачкалинский филиал МАДГТУ, 2011 г. – 24стр.

4. Эверстова Т.Л. Комплекс задач практического содержания как средство повышение интереса учащихся 9 класса к изучению математики (на примере темы «Квадратичная функция») (Ссылка на статью https://sibac.info/studconf/hum/xxvii/40129)

Скачано с www.znanio.ru