Урок_2_Решение текстовых задач_Методические рекомендации

Методические рекомендации к уроку №2

темы/подраздела « Квадратичная функция и ее график »

раздела « Квадратичная функция»

Тема урока: Решение текстовых задач

Цель обучения:

8.4.2.3 использовать квадратичную функцию для решения прикладных задач;

8.4.3.1 составлять математическую модель по условию задачи.

Учащиеся рассмотрят решение прикладных задач с помощью составления и/или исследования математической модели в виде квадратичной функции.

Методические рекомендации по организации урока. Рекомендации по формативному оцениванию

В начале урока учащимся предлагается задание выделение квадрата двучлена из квадратного трехчлена. Учащиеся должны записывать ответы на мини-досках. На слайдах будут продемонстрированы верные ответы, чтобы учащиеся могли сразу оценить свое понимание материала.

Письменная работа начинается с совместного разбора задания на применение свойств и графика квадратичной функции при решении практической задачи. Затем учащиеся развивают этот навык при решении задачи в группах.

Для самостоятельного решения задач предлагаются дифференцированные задания. В соответствии с планом урока учитель сам распределяет задания. Однако можно предложить учащимся весь список из трех задач, предоставив им возможность самостоятельно определить подходящий для них уровень сложности. Учащиеся на этом этапе будут самостоятельно оценивать свою работу по образцам правильных решений. Даже если ученик затрудняется в решении, изучение этих образцов (они подходят к образцам без ручек или карандашей), а затем и воспроизведение решения в тетради будет полезным для него.

Во время рефлексии учитель получит полезную информацию, в соответствии с которой он может внести изменения в план следующего урока.

Дополнительные разноуровневые задания

1.      Постройте график функции и запишите по крайней мере 5 ее свойств:

а) ;

ә) .

2.      Постройте график данной функции и задайте ее одной формулой:

Ответы и решения

Задание 1.

Если подбросить мяч вертикально вверх, то высота (h), на которой находится мяч через t секунд полета вычисляется по формуле .

а) Через сколько секунд мяч достигнет максимальной высоты?

б) На какую максимальную высоту поднимется мяч?

Решение.

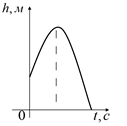
а) Мяч достигнет максимальной высоты при t = 1 (с) (абсцисса вершины параболы).

б) Максимальную высоту, на которую поднимется мяч, можно вычислить, подставив в формулу значение t, равное 1:

h =  – 5 + 10 + 1,5 = 6,5 (м).                              

Уровень В

Задание 2.

Мяч подбросили вертикально вверх с высоты 1,4м с начальной скоростью 6 м/сек. Высота (h), на которой находится мяч через t секунд полета вычисляется по формуле  где g ≈ 10 (м/с²),  – начальная скорость,  – начальная высота.

а) Через сколько секунд мяч достигнет максимальной высоты?

б) На какую максимальную высоту поднимется мяч?

в) Через сколько секунд мяч упадет на землю?

Решение.

Составим функцию :  , т.е. 

а) Определим абсциссу вершины параболы: t = 0,6(с).

б) Определим ординату вершины параболы:

в) Решим уравнение , найдем искомое значение t = 1,4 (с).

Уровень С

Задание 3.

Во время эпидемии гриппа доктор стал вести учет количества больных гриппом. Данные врача можно математически описать формулой , где N – число больных в зависимости от числа дней , прошедших с начала ведения наблюдения.

а) Через сколько дней после начала ведения учета доктор зафиксировал наибольшее количество больных гриппом?

б) Через сколько дней доктору удалось справиться с эпидемией?

в) Можно ли определить, когда началась эпидемия?

Решение.

а) Для определения наибольшего количества больных гриппом нужно найти первую координату вершины параболы: t = 5.

б)

t = 14.

в) Второй корень t = -4  уравнения  показывает, что эпидемия началась за 4 дня до того, как доктор начал вести свои записи.

Список полезных ссылок и литературы

1. Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Феоктистов И.Е. Алгебра. 9 класс : учеб. для учащихся общеобразоват. учреждений.  – М.: Мнемозина, 2010

2.  Мордкович А. Г. Алгебра. 8 кл.: Учеб. для общеобразоват. учреждений. – М.: Мнемозина, 2001.