Урок_3_Решение текстовых задач_Методические рекомендации (1)

Методические рекомендации к уроку №3

темы/подраздела « Квадратичная функция и ее график »

раздела « Квадратичная функция»

Тема урока: Решение текстовых задач

Цель обучения:

8.4.2.3 использовать квадратичную функцию для решения прикладных задач;

8.4.3.1 составлять математическую модель по условию задачи.

На данном уроке учащиеся продолжат работу по развитию навыка решения задач с использованием квадратичной функции.

Методические рекомендации по организации урока. Рекомендации по формативному оцениванию

В начале урока учащимся предлагается задание на составление формулы квадратичной функции и применение ее свойств. Важно организовать свободную дискуссию учащихся в процессе обсуждения.

Письменная работа начинается с совместного разбора задания на составление уравнения функции и поиска ответа на вопрос задачи. Интересным и несколько неожиданным является вопрос о геометрическом истолковании полученного ответа.

Для работы в парах предлагаются еще две задачи практического содержания, связанные с площадями.

Дополнительные задания направлены на развитие критического мышления учащихся. Однако их решение не требует от учащихся каких-то дополнительных знаний, выходящих за рамки программы.

Ответы и решения

Задания для устной работы

1) По графику функции  определите коэффициенты b и c.

Решение.

Коэффициент с было бы легко найти, но на оси Oy нет делений. Однако показаны точки пересечения с осью Ox. А это корни уравнения : . .

Старший коэффициент равен 1. Тогда по теореме Виета имеем:

Отсюда, b  = -(-1 + 4) = -3 и c = -1 · 4 =- 4.

2) Для некоторой реки экспериментально установили следующую зависимость скорости течения реки v(м/с) от глубины h (м):

Найдите максимальную глубину реки (т.е. глубину, где v = 0) и глубину с максимально сильным течением.

Решение.

Для решения задачи достаточно выяснить, какое значение -наибольшее или наименьшее - принимает функция. Это значение равно ординате вершины параболы.

Максимальная глубина 4 м.

Наибольшая скорость 9 м/с при h=1м.

Фронтальная работа с классом

3) Площадь S прямоугольника с периметром, равным 16 см, является функцией длины его основания х. Задайте эту функцию формулой. Определите, при каком значении х функция принимает наибольшее значение. Дайте геометрическое истолкование ответа.

Решение.

Одна сторона прямоугольника равна х см, тогда вторая – (8 – х) см. Следовательно,  или .

Ветви параболы направлены вниз, значит наибольшее значение функция принимает в вершине параболы и это значение равно ординате вершины:

.

Итак, при х = 4 значение S максимально.

Если одна сторона прямоугольника равна 4 см, тогда вторая сторона также 4 см, значит, из всех прямоугольников с периметром, равным 16 см, наибольшую площадь имеет квадрат.

Работа в парах

4) Фермер имеет 120 м ограждения. Он хочет оградить прямоугольный участок земли, который будет примыкать одной стороной к дому. Поэтому ему нужно поставить забор только вокруг трех сторон участка. Найдите максимальную площадь, которую может оградить фермер. Какие размеры будет иметь огражденный участок?

Решение.

Пусть х м – стороны участка, прилежащие к дому, тогда сторона, противолежащая дому, будет иметь длину  м. Площадь S участка можно вычислить по формуле:

 или . Зависимость S от x является квадратичной функцией, причем . Значит функция принимает максимальное значение в вершине параболы. Найдем ее координаты:

.

Итак, максимальная площадь участка 1800 кв.м., размеры участка 30 м на 60 м (120 - 2·30).

5) Для стока воды с крыши здания устанавливают специальные металлические или пластиковые желоба. При изготовлении желоба необходимо учитывать принцип экономичности и выбрать оптимальные размеры для обеспечения максимальной пропускной способности.

Пусть периметр поперечного сечения желоба равен 40 см.

а) Какие размеры должен иметь желоб, чтобы получить максимальный слив, если поперечное сечение имеет форму прямоугольника?

б) Каков радиус поперечного сечения, если оно имеет форму полукруга?

в) Какое сечение является наиболее оптимальным?

Решение.

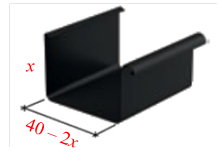а) Пусть  см – высота боковых стенок желоба, тогда площадь поперечного сечения желоба

Чтобы найти ответ на вопрос задачи, необходимо установить, при каких значениях  полученная функция           принимает наибольшее значение. Так как коэффициент  , то функция    принимает максимальное значение при .

Следовательно, высота стенок должна быть равна 10 см, а ширина дна желоба – 20 см.

(Источник картинки http://www.roof-n-roll.ru.opt-images)

б) Если радиус полукруга равен R, а периметр равен 40 см, то . Отсюда, см.

(Источник картинки: https://profstal.by/wp-content/uploads)

в)  и - площади поперечных сечений (в кв. см) прямоугольной и полукруглой форм соответственно. Очевидно, что желоба с полукруглым сечением имеют большую пропускную способность. К тому же желоба такой формы более устойчивы к механическим нагрузкам, например, при сходе снега.

Дополнительные разноуровневые задания

Уровень А – вопросы а) и б).

Уровень В – вопрос в).

Уровень С – вопрос г).

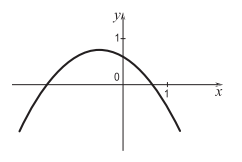Дан график квадратичной функции .

Верно ли утверждение:

а) ;

б) ;

в) ;

г) ?

Ответ: а) да; б) нет; в) нет) г) да.

Решение.

г) Выражение  является значением данной функции при х = 3. Как видно из графика, f(3) < 0.

Список полезных ссылок и литературы

1. Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Феоктистов И.Е. Алгебра. 9 класс : учеб. для учащихся общеобразоват. учреждений.  – М.: Мнемозина, 2010

2.  «Кенгуру» - выпускникам 9 класса. Тест готовности к продолжению образования.

3. Курбанов К.О. Некоторые прикладные задачи по высшей математике (методическое пособие). – Махачкала: Махачкалинский филиал МАДГТУ, 2011 г. – 24стр.

4. Эверстова Т.Л. Комплекс задач практического содержания как средство повышение интереса учащихся 9 класса к изучению математики (на примере темы «Квадратичная функция») (Ссылка на статью https://sibac.info/studconf/hum/xxvii/40129)

Скачано с www.znanio.ru