Урок_3_Решение текстовых задач_Методические рекомендации

Методические рекомендации к уроку №3

темы/подраздела « Квадратичная функция и ее график »

раздела « Квадратичная функция»

Тема урока: Решение текстовых задач

Цель обучения:

8.4.2.3 использовать квадратичную функцию для решения прикладных задач;

8.4.3.1 составлять математическую модель по условию задачи.

На данном уроке учащиеся продолжат работу по развитию навыка решения задач с использованием квадратичной функции.

Методические рекомендации по организации урока. Рекомендации по формативному оцениванию

В начале урока учащимся предлагается тестовые задания для организации повторения пройденного материала. Учитель заранее готовит сигнальные карточки трех цветов для каждого ученика. Их использование позволит учителю быстро оценить понимание учащимися определенного материала. Допущенные ошибки сразу анализируются.

Затем проводится письменная работа, она с совместного разбора задания на составление уравнения функции и поиска ответа на вопрос задачи. Учитель вовлекает всех учащихся в диалог. Для первоначального закрепления учащиеся решают задачу в группах. Здесь нужно нацелить их на то, что каждый ученик после обсуждения должен уметь объяснить решение задачи свой группы. Процесс объяснения другим учащимся позволит глубже разобраться в решении. Также здесь нужно поощрять учащихся, задающих вопросы. Учитель обходит класс, слушает объяснения, помогает в корректном применении математического языка.

Два задания подготовлены для самостоятельного решения учащимися. Учитель обходит класс, дает советы учащимся. Он может также привлекать других учащихся для консультирования тех, кто испытывает затруднения.

Ответы и решения

Мост Голден Гейт через пролив Золотые ворота находится в Сан-Франциско (США). Мост построен по проекту инженера Йозефа Штрауса. Строительство началось в 1933 году и было закончено через 4 года. Мост установил два рекорда: как самый длинный и как самый высокий мост.

Длина основного пролета моста (расстояние между опорами) 1280 м, высота опор над уровнем проезжей части моста – 160 м. Кабель, поддерживающий мост, имеет форму параболы и касается проезжей части в середине пролета. На какой высоте находится кабель на расстоянии 200 м от опоры моста?

Решение.

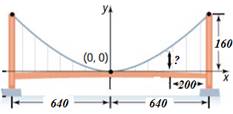Построим координатную плоскость, так чтобы ось х проходила вдоль проезжей части моста, а ось у – вдоль оси симметрии. Тогда вершина параболы имеет координаты (0, 0), значит функция задается формулой .

Точка (640, 160) – расположена на одной из опор, отсюда  и , .

Тогда уравнение параболы имеет вид: .

Кабель находится на расстоянии 200 м от опоры моста, следовательно, в 440 м от вершины параболы.

Ответ: 75,625 м.

Задание для группы 1

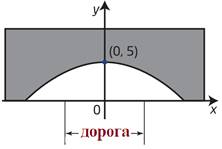
Дорога проходит под параболической аркой, как показано на рисунке. Самая высокая часть арки – 5 м. Ширина дороги – 10м, а высота – 4 м. Составьте квадратичную функцию, задающую форму арки.

Решение.

Запишем уравнение параболы в виде . Координаты вершины параболы (0; 5), тогда

Ширина дороги – 10м, а высота – 4 м, значит парабола проходит через точку .

Ответ: .

Задание для группы 2

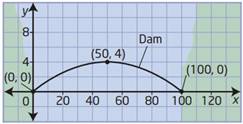
Небольшие мосты имеют форму параболы. На рисунке представлен один из таких мостов. Составьте уравнение параболы, определяющей форму этого моста.

Решение.

Запишем уравнение параболы в виде . Вершина имеет координаты (50; 4).

Парабола проходит через точки  и .

Ответ: .

Задание для группы 3

Длина моста 400 м, а высота опор 75 м. Напишите уравнение параболы, являющейся моделью для подвесного кабеля, удерживающего этот мост.

Решение.

Построим координатную плоскость, так чтобы ось х проходила вдоль проезжей части моста, а ось у – вдоль оси симметрии. Тогда вершина параболы имеет координаты (0, 0), значит функция задается формулой .

Парабола проходит через точку (200; 75), тогда  и , .

Тогда уравнение параболы имеет вид:

Индивидуальная работа

1. Тело брошено вертикально вверх. Высота (h), на которой находится тело через t секунд полета, вычисляется по формуле  где g ≈ 10 (м/с²),  – начальная скорость,  – начальная высота.

Составьте формулу, задающую эту зависимость, если h₀= 20, v₀ = 15 и постройте график.

Используя график, ответьте на вопросы:

а) Сколько времени тело двигалось вверх?

б) Сколько времени тело двигалось вниз?

в) На какую максимальную высоту поднялось тело?

г) В течении какого времени тело находилось на высоте более 20 м?

Решение.

Функция имеет вид  .

а)  c

б)

Через 4 с тело упало на землю.

4-1,5 = 2,5

Тело двигалось вниз 2,5 с.

в)

г)

Ответ: Тело находилось на высоте более 20 м в течение 3 с.

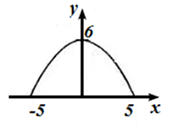
2. Двух полосная дорога со встречным движением проходит под аркой шириной 10 м. Самая высокая точка арки расположена на высоте 6 м. Сможет ли грузовик, высота которого 4,5 м, а ширина 3 м, проехать под этой аркой? Ответ объясните.

Решение.

Если расположить координатную плоскость, так чтобы ось х проходила вдоль проезжей части дороги, а ось у – вдоль оси симметрии, тогда вершина параболы имеет координаты (0, 6). Парабола проходит через точки и . Тогда ее можно задать формулой:

Подставив координаты точки  найдем значение а:

Ширина грузовика 3 м, тогда при  имеем:

 .

Ответ: Грузовик может проехать под этой аркой.

Дополнительные задания

Уровень В

Найдите наибольшее или наименьшее значение функции.

a)         .

b)         .

c)                 

Уровень С

Определите коэффициенты функции , если:

а)  при , а  наименьшее значение функции, равное -12, достигается при ;

б) , наибольшее значение функции, равное 25, достигается при ;

в) наименьшее значение функции, равное 7, достигается при , а при  значение функции равно 15.

Список полезных ссылок и литературы

1. Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Феоктистов И.Е. Алгебра. 9 класс : учеб. для учащихся общеобразоват. учреждений.  – М.: Мнемозина, 2010

2. Виленкин Н.Я., Сурвилло Г.С. Алгебра. 9 класс. учеб. Для учащихся с углубленным изучением математики. / 7-е изд. - М.: Просвещение, 2006.

3. Алексеевский С., Применение свойств квадратичной функции http://uslide.ru/matematika/32964-primenenie-svoystv-kvadratichnoy-funkcii.html

https://studbooks.net/1869914/pedagogika/ispolzovanie_svoystv_kvadratichnoy_funktsii_reshenii_praktiko_orientirovannyh_zadach_kurse_matematiki

Скачано с www.znanio.ru