Урок_3_Решение текстовых задач_План урока (1)

Краткосрочный план

Раздел 8.3А: Квадратичная функция

Школа:

Дата:

ФИО учителя:

Класс: 8

Количество присутствующих:

Количество отсутствующих:

Тема урока

Решение текстовых задач

Урок №3 серии из 6 уроков

Тип урока

Урок закрепления знаний и навыков

Цели обучения (ссылка на учебную программу)

8.4.2.3

использовать квадратичную функцию для решения прикладных задач;

8.4.3.1

составлять математическую модель по условию задачи

Цели урока

Использовать график и свойства квадратичной функции для решения задач

Критерии оценивания

Языковые цели

Учащиеся объясняют, как использовать свойства или график квадратичной функции в конкретной ситуации.

Предметная лексика и терминология

− квадратичная функция

− значение функции

− аргумент

− значение аргумента

− наибольшее / наименьшее значение

− математическая модель

Серия полезных фраз для диалога/письма

Наибольшее / наименьшее значение функция достигает в вершине параболы.

Введем переменную.

Обозначим … буквой х.

Выразим … через х.

Привитие ценностей

Функциональная грамотность - умение применять полученные знания и навыки для личных, социальных, экономических целей.

Осуществляется через содержание урока.

Межпредметные связи

Физика, экономика

Навыки использования ИКТ

Презентация

Предварительные знания

Учащиеся знают свойства квадратичной функции, умеют определять их по графику квадратичной функции.

Ход урока

Этапы урока

Запланированная деятельность на уроке

Ресурсы

Начало урока

1мин

7 мин

2 мин

Организационный момент

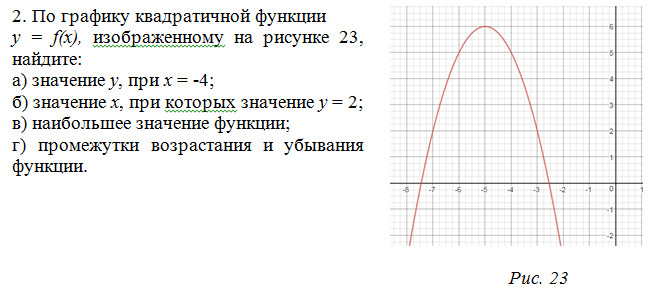
Актуализация знаний

1) По графику функцииопределите коэффициентыbиc.

2) Для некоторой реки экспериментально установили следующую зависимость скорости течения реки v(м/с) от глубины h (м):

Найдите максимальную глубину реки (т.е. глубину, где v = 0) и глубину с максимально сильным течением.

Обсуждение домашнего задания

Организовать обсуждение вопросов по домашнему заданию.

Презентация

Слайды 1-2

Слайды 3-4

Тетради учащихся

Середина урока

10 мин

15 мин

5 мин

Решение задач. Обсуждение в классе

Обратить внимание учащихся на то, что при решении различных практических задач математическими способами создается математическая модель задачи. Обычно они получали модель в виде уравнений или неравенств, или их систем. На этом уроке будут рассмотрены задачи, для решения которых будут составлены функциональные зависимости и исследованы свойства полученных функций.

Организовать обсуждение решения следующей задачи:

3) Площадь Sпрямоугольника с периметром, равным 16 см, является функцией длины его основания х. Задайте эту функцию формулой. Определите, при каком значении х функция принимает наибольшее значение. Дайте геометрическое истолкование ответа.

Решение.

Одна сторона прямоугольника равна х см, тогда вторая – (8 – х) см. Следовательно,  или .

Ветви параболы направлены вниз, значит наибольшее значение функция принимает в вершине параболы и это значение равно ординате вершины:

.

Итак, при х = 4 значение S максимально.

Если одна сторона прямоугольника равна 4 см, тогда вторая сторона также 4 см, значит, из всех прямоугольников с периметром, равным 16 см, наибольшую площадь имеет квадрат.

Работа в парах

4) Фермер имеет 120 м ограждения. Он хочет оградить прямоугольный участок земли, который будет примыкать одной стороной к дому. Поэтому ему нужно поставить забор только вокруг трех сторон участка. Найдите максимальную площадь, которую может оградить фермер. Какие размеры будет иметь огражденный участок?

5) Для стока воды с крыши здания устанавливают специальные металлические или пластиковые желоба. При изготовлении желоба необходимо учитывать принцип экономичности и выбрать оптимальные размеры для обеспечения максимальной пропускной способности.

Пусть периметр поперечного сечения желоба равен 40 см.

а) Какие размеры должен иметь желоб, чтобы получить максимальный слив, если поперечное сечение имеет форму прямоугольника?

б) Каков радиус поперечного сечения, если оно имеет форму полукруга?

в) Какое сечение является наиболее оптимальным?

Дополнительное задание

Дан график квадратичной функции .

Верно ли утверждение:

а) ;

б) ;

в) ;

г) ?

Ответ: а) да; б) нет; в) нет) г) да.

Слайд 5

Слайды 6-8

Приложение 1

«Кенгуру» - выпускникам 9 класса. Тест готовности к продолжению образования. 2008 г.

Конец урока

3 мин

2 мин

Рефлексия

Сегодня я узнал….

У меня получилось … .

Было трудно….

Меня удивило….

Я хочу отметить, что … .

Домашнее задание

1) Для некоторой компании по производству компьютерных деталей прибыль, полученная от призводства, можно выразить функцией , где- число деталей, произведенных за неделю.

а) Постройте график данной функции.

б) Запишите координаты точек пересечения графика с осью Ох. Какую информацию отражают эти координаты?

в)Запишите координаты точек пересечения графика данной функции с осью Оу. Какую информацию отражают эти координаты?

г) Найдите координаты вершины параболы. Какую информацию отражают эти координаты?

2) Верно ли утверждение: если уравнение  имеет два корня, то уравнение  тоже имеет два корня? Ответ обоснуйте.

Слайд 9

Дифференциация – каким образом Вы планируете оказать больше поддержки? Какие задачи Вы планируете поставить перед более способными учащимися?

Оценивание – как Вы планируете проверить уровень усвоения материала учащимися?

Здоровье и соблюдение техники безопасности

Учащиеся будут работать в парах, чтобы иметь возможность для поддержки более сильными учениками.

Учащиеся будут оценивать друг друга во время решения задач.

Учитель будет обходить класс, предоставляя устные комментарии.

Кабинет проветрен. Желательно в середине урока выполнить несколько упражнений для разминки учащихся.

Рефлексия по уроку

Были ли цели урока/цели обучения реалистичными?

Все ли учащиеся достигли ЦО?

Если нет, то почему?

Правильно ли проведена дифференциация на уроке?

Выдержаны ли были временные этапы урока?

Какие отступления были от плана урока и почему?

Используйте данный раздел для размышлений об уроке. Ответьте на самые важные вопросы о Вашем уроке из левой колонки.

Общая оценка

Какие два аспекта урока прошли хорошо (подумайте как о преподавании, так и об обучении)?

1:

2:

Что могло бы способствовать улучшению урока (подумайте как о преподавании, так и об обучении)?

1:

2:

Что я выявил(а) за время урока о классе или достижениях/трудностях отдельных учеников, на что необходимо обратить внимание на последующих уроках?