Урок_4_Приложение 2_Теоретический материал

Лист 1

График и свойства квадратичной функции

Любую квадратичную функцию  можно задать формулой вида .

Докажем это.

Выделив из квадратного трехчлена  квадрат  двучлена, получим

где .

Обозначив  буквой m, a   - буквой n, получим

Следовательно, график функции  можно получить из графика функции  с помощью двух параллельных переносов — сдвига вдоль оси х и сдвига вдоль оси у.

График функции  - парабола. Значит, и графиком функции  является парабола с вершиной в точке (m; n), где ,  . Осью симметрии параболы является прямая х = m.

Лист 2

Учитывая что графиком функции  является парабола с вершиной в точке (m; n), где ,  , можно схематически изобразить график квадратичной функции. На рисунке показано, какой вид имеют эти графики в зависимости от знака дискриминанта D при а > 0.

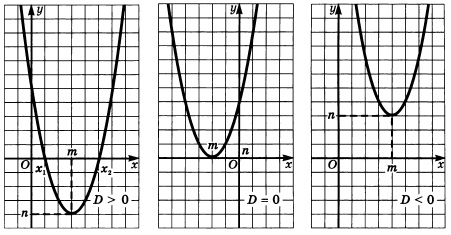
Перечислим свойства функции  при а > 0:

1. Область определения функции — множество действительных чисел.

2. Если D > 0, то функция обращается в нуль при  и . Если D=0, то она обращается в нуль при  . Если D < 0, то функция нулей не имеет.

3. Если D > 0, то функция принимает положительные значения в каждом из промежутков (-∞;) и (; +∞) и отрицательные значения в промежутке (; ). Если D=0, то функция принимает положительные значения при любых , кроме . Если D < 0, то функция положительна на всей области определения.

4. Функция убывает на промежутке  и возрастает на промежутке . При  функция принимает наименьшее значение, равное .

5. Область значений функции – множество .

Лист 3

На рисунке ниже показано, какой вид имеют графики квадратичной функции при

 а < 0 и в зависимости от знака D.

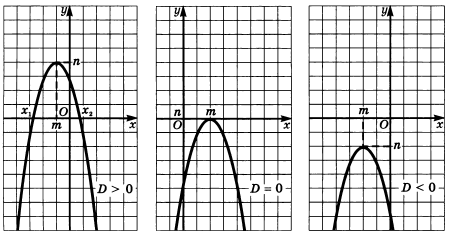
Перечислим свойства функции  при а < 0:

1. Область определения функции — множество действительных чисел.

2. Если D > 0, то функция обращается в нуль при  и . Если D=0, то она обращается в нуль при  . Если D < 0, то функция нулей не имеет.

3. Если D > 0, то функция принимает положительные значения в промежутке (; ) и отрицательные значения в каждом из промежутков (-∞;) и (; +∞). Если D=0, то функция принимает отрицательные значения при любых , кроме . Если D < 0, то функция отрицательна на всей области определения.

4. Функция возрастает на промежутке  и убывает на промежутке . При  функция принимает наибольшее значение, равное .

5. Область значений функции – множество .

Лист 4

При построении графика квадратичной функции, заданной формулой , целесообразно найти нули функции, координаты вершины параболы, координаты точки пересечения параболы с осью у и точки, симметричной ей относительно оси  симметрии параболы. Затем следует отметить эти точки в координатной плоскости и провести через них плавную непрерывную линию.

Заметим, что в тех случаях, когда парабола не имеет общих точек с осью х или пересекает ось у в точке, достаточно удаленной от начала координат, для построения параболы используют другие точки, симметричные относительно ее оси.

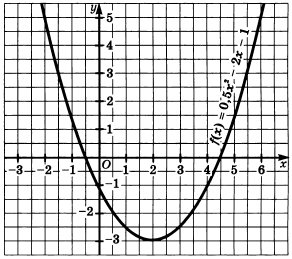
Пример. Построим график функции .

Найдем нули функции. Решив уравнение , получим, что  и . Значит, парабола пересекает ось х в точках, абсциссы которых приближенно равны -0,5 и 4,5.

Вычислим координаты m и n вершины параболы. Абсциссу m найдем по формуле , а ординату n найдем, подставив в формулу  вместо х значение m. Имеем:

Положив х = 0, найдем координаты точки пересечения параболы с осью у. Получим точку (0; -1). Симметричная ей точка относительно оси симметрии параболы имеет координаты (4; -1).

Построим эти точки и, учитывая направление ветвей параболы, проведем через них непрерывную линию. Получим график функции .