Урок_4_Решение текстовых задач_Методические рекомендации (1)

Методические рекомендации к уроку №4

темы/подраздела «Квадратичная функция и ее график»

раздела «Квадратичная функция»

Тема урока: Решение текстовых задач

Цель обучения:

8.4.2.3 использовать квадратичную функцию для решения прикладных задач;

8.4.3.1 составлять математическую модель по условию задачи.

На данном уроке учащиеся продолжат работу по развитию навыка решения задач с использованием свойств и графика квадратичной функции.

Методические рекомендации по организации урока. Рекомендации по формативному оцениванию

Для повторения тем Квадратичная функция и Квадратные уравнения предлагается работа с утверждениями о функциях или уравнениях. Для некоторых утверждений довольно легко определить к какой категории они относятся, но некоторые вопросы заставят учащихся поразмышлять, критически оценить различные возможные ситуации. Можно эти утверждения обсудить всем классом.

Далее учащиеся изучают решение и оформление практической задачи. В дальнейшей устной и письменной работе они могут использовать это решение как образец. Учитель может задавать членам группы уточняющие вопросы, чтобы убедиться, что все учащиеся вовлечены в обсуждение решений предложенных задач.

Дополнительные задания также имеют практический характер, но не связаны с квадратичной функцией. Это сделано намеренно, учащиеся должны научиться определять, какую математическую модель лучше использовать в той или иной ситуации.

Ответы и решения

Задания для устной работы

Фронтальная работа с классом

1) Нормандское окно имеет форму прямоугольника, завершенного полукругом. В архитектуре часто используется такая форма окна. Дан периметр нормандского окна P. Каковы должны быть его размеры, чтобы оно пропускало наибольшее количество света?

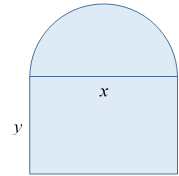
Решение.

Пусть x – основание, а y – высота прямоугольника, тогда . Выразим высоту прямоугольника:

. Следовательно, площадь окна выражается формулой

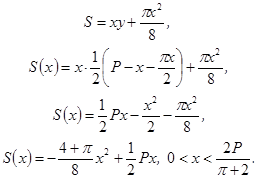
Площадь представляет собой квадратичную функцию, старший коэффициент которой отрицателен. Следовательно, свое наибольшее значение она будет принимать при  или .

Т.к.  и то

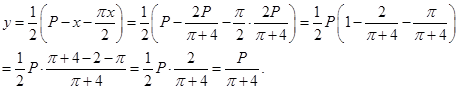
Итак, наибольшую площадь при заданном периметре нормандское окно будет иметь при  и .

Ответ: Размеры прямоугольной части окна должны быть равны

2) Производственная фирма решила построить новый склад для хранения сырья. Высота склада должна быть равной 4 м. Материала, используемого для покрытия наружных стен, будет достаточно, чтобы при такой высоте покрыть 36 метров стены в длину. Какими должны быть размеры склада (в виде прямоугольного параллелепипеда), чтобы он имел наибольший объём?

Решение.

Пусть х м длина склада, тогда ширина склада – (18 – х) м, а объем равен

 или .

Максимальное значение данной функции достигается в вершине параболы.

.

Следовательно, наибольший объем будет иметь склад с размерами 8 м на 8 м.

3) Струя воды фонтана достигает наибольшей высоты 1,2 м на расстоянии 1 м от точки О выхода струи. Найти высоту струи на расстоянии 0,6 м от точки О.                                                                             

Источник картинки:

http://sobinova44.ru/sites/default/files/fontan.JPG

Решение.

Введем систему координат. Пусть точка О – начало отсчета. Тогда вершина параболы имеет координаты (1; 1,2), а уравнение параболы имеет вид . Поскольку точка О(0; 0) принадлежит параболе, то а = - 1,2. Найдем значение функции в точке х = 0,6:

.

Ответ: 1 м.

Домашнее задание

4) Из курса физики известно, что высота h, на которой находится предмет, брошенный вертикально вверх, является квадратичной функцией времени полёта t. Она задается формулой , где  - начальная скорость предмета,  - высота, с которой прошен предмет, g – ускорение свободного падения, .

Мяч бросили вертикально вверх с высоты 3 м с начальной скоростью 9м/с. На какую максимальную высоту поднялся мяч и когда он упал на землю?

Решение.

Подставив в эту формулу значения  и , получим . Максимальная высота достигается в вершине параболы, значит

(м).

Чтобы узнать, когда мяч упал на землю, т. е. чтобы найти значение t при котором h=0, решим уравнение .

 ;  ; .

Условию задачи удовлетворяет только положительный корень уравнения. Значит, мяч упал на землю после 2,1 с полёта.

График функции  изображён на рисунке.

Дополнительные разноуровневые задания

Уровень В

Если автомобиль движется со скоростью 120 км/час, то на 100 км пути расходуется 6 л топлива, а если он движется со скоростью 150 км/час, то на 100 км пути расходуется 9 л топлива. Верно ли утверждение:

а) При скорости 120 км /час 8 литров топлива хватит на 150 км пути.

б) На одном и том же количестве топлива, двигаясь со скоростью 120 км/час, можно проехать на 50% больший путь, чем двигаясь со

скоростью 150 км/час.

в) При скорости 120 км/час 5 литров топлива хватит на 45 минут езды.

г) Если автомобиль проехал 300 км, потратив 21 литр топлива, и при этом x км проехал со скоростью 120 км/час, а остальной путь — со скоростью 150 км/час, то .

Ответ: а) нет; б) да; в) нет; г) да.

Список полезных ссылок и литературы

1. Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Феоктистов И.Е. Алгебра. 9 класс : учеб. для учащихся общеобразоват. учреждений.  – М.: Мнемозина, 2010

2.  «Кенгуру» - выпускникам 9 класса. Тест готовности к продолжению образования.

3. Курбанов К.О. Некоторые прикладные задачи по высшей математике (методическое пособие). – Махачкала: Махачкалинский филиал МАДГТУ, 2011 г. – 24стр.

4. Эверстова Т.Л. Комплекс задач практического содержания как средство повышение интереса учащихся 9 класса к изучению математики (на примере темы «Квадратичная функция») (Ссылка на статью https://sibac.info/studconf/hum/xxvii/40129)

Скачано с www.znanio.ru