Урок_4_Решение текстовых задач_Методические рекомендации

Методические рекомендации к уроку №4

темы/подраздела «Квадратичная функция и ее график»

раздела «Квадратичная функция»

Тема урока: Решение текстовых задач

Цель обучения:

8.4.2.3 использовать квадратичную функцию для решения прикладных задач;

8.4.3.1 составлять математическую модель по условию задачи.

На данном уроке учащиеся продолжат работу по развитию навыка решения практических задач с использованием свойств и графика квадратичной функции.

Методические рекомендации по организации урока. Рекомендации по формативному оцениванию

Для создания благоприятной обстановки урок начинается с игры «Атомы и молекулы», где атомы – учащиеся, молекулы – группы, которые они образуют. Игра должна проходить быстро, чтобы учащиеся собирались в группы случайным образом, можно включить веселую музыку. Ученики в процессе будут поделены на группы по 3 человека.

Для повторения темы Квадратичная функция предлагается работа на установление соответствия с последующей взаимопроверкой. В приложении 1 имеется два варианта похожих карточек, расположенные в двух столбцах. Взаимопроверку можно организовать так, чтобы группы с одинаковыми комплектами карточек проверяли друг друга, но учащимся более интересным будет проверка заданий из другого комплекта карточек.  Учитель может задавать членам группы уточняющие вопросы, чтобы убедиться, что все учащиеся вовлечены в обсуждение предложенных заданий.

Учащиеся также будут работать самостоятельно, здесь возможен различный темп работы, поэтому предусмотрено дополнительные задания, которые предложены ниже.

Дополнительные разноуровневые задания

Уровень А

Камень брошен вертикально вверх. Пока камень не упал, высота его над землей, описывается по формуле, где- высота в метрах,-время в секундах, прошедшее со времени броска. Сколько секунд камень находился на высоте не менее 72 м?

Уровень В

Для того, чтобы найти высоту, на которой находится спортсмен при прыжке с трамплина в каждый момент времени t, используют формулу  . Здесь t  показывает время в секундах, h - высоту в метрах.

Какова высота этого трамплина7

Через сколько секунд спортсмен войдет в воду?

Ответы и решения

1. Производительность труда в течение рабочего времени меняется в зависимости от времени работы по формуле.

Постройте график функции, считая рабочий день равным 8 ч.

а) В какой момент времени производительность труда достигает максимума?

б) Укажите промежуток рабочего дня, во время которого производительность труда растет?

в) Укажите промежуток рабочего дня, во время которого производительность труда падает?

г) В какое время производительность выше: через 1 ч или через 5 ч после начала рабочего дня?

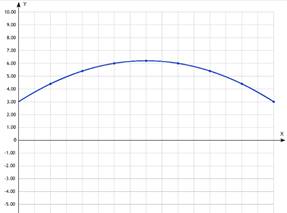Решение.

а) В середине рабочего дня.

б) В первой половине рабочего дня.

в) Во второй половине рабочего дня.

г) Точка, соответствующая значению t = 1, расположена ниже точки соответствующей значению t = 5, следовательно, через 5 ч после начала рабочего дня производительность была выше.

2. В рамках мероприятий по охране природы ведется учет числа оленей одной из популяций. С начала учета число оленей (N) изменяется по формуле , где t выражено в годах.

а) Как изменилось число оленей за первые 10 лет?

б) Через сколько лет число оленей было максимальным и каким было это число?

в) Через сколько лет после начала учета популяция оленей может исчезнуть?

Решение.

а) , .

80 – 50 = 30, значит популяция увеличилась на 30 особей.

б) Вершина параболы имеет координаты t = 20 и , следовательно, через 20 лет число оленей было максимальным и равнялось 90.

в)

t = 50 – положительный корень уравнения.

Популяция оленей может исчезнуть через 50 лет после начала учета.

Индивидуальная работа

Учащиеся работают самостоятельно, учитель обходит класс, просматривает решения учащихся, дает рекомендации по улучшению решений, задает наводящие вопросы.

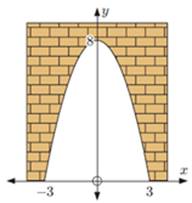
1) Грузовик должен пройти через показанный параболический туннель. Единицы измерения - метры. Высота грузовика равна 5 м, а ширина 4 м.

а) Найдите квадратичную функцию, описывающую форму туннеля.

б) Определите, пройдет ли грузовик через туннель.

Решение.

а)

 Точка (0; 8) принадлежит графику, тогда

,

.

б) , значит грузовик проедет через туннель.

2) Камень брошен вертикально вверх. Пока камень не упал, высота его над землей, описывается по формуле, где- высота в метрах,-время в секундах, прошедшее со времени броска. Сколько секунд камень находился на высоте не менее 28 м?

Решение. 

– 5t² + 39t = 28,  

5t² + 39t – 28 = 0,  

t₁ = 0,8,  t₂ = 7.                 

 7 – 0,8 = 6,2, т.е. 6.2 с камень находился на высоте не менее 28 м.

Список полезных ссылок и литературы

1.      Мордкович А. Г. Алгебра. 8 кл.: Учеб. для общеобразоват. учреждений. – М.: Мнемозина, 2001.

2.      Виленкин Н.Я., Сурвилло Г.С. Алгебра. 9 класс. учеб. Для учащихся с углубленным изучением математики. / 7-е изд. - М.: Просвещение, 2006.

3.      Алексеевский С., Применение свойств квадратичной функции http://uslide.ru/matematika/32964-primenenie-svoystv-kvadratichnoy-funkcii.html

4.       https://studbooks.net/1869914/pedagogika/ispolzovanie_svoystv_kvadratichnoy_funktsii_reshenii_praktiko_orientirovannyh_zadach_kurse_matematiki

Скачано с www.znanio.ru