Урок_5_Решение текстовых задач_Методические рекомендации (1)

Методические рекомендации к уроку №5

темы/подраздела « Квадратичная функция и ее график »

раздела « Квадратичная функция»

Тема урока: Решение текстовых задач

Цель обучения:

8.4.1.2 знать свойства и строить графики квадратичных функций вида y=a(x-m)², y=ax²+n, y=a(x-m)²+n, a≠0;

8.4.1.3 знать свойства и строить график квадратичной функции вида ;

8.4.2.3 использовать квадратичную функцию для решения прикладных задач;

8.4.3.1 составлять математическую модель по условию задачи.

На данном уроке будет проведена работа по обобщению и систематизации знаний и умений учащихся по данному разделу.

Методические рекомендации по организации урока. Рекомендации по формативному оцениванию

Учащиеся будут разделены на группы. В начале урока будет организовано повторение и углубление знаний учащихся. Учащиеся должны составить вопросы, можно разрешить учащимся использовать различные источники, это поможет им повторить детали и составить более разнообразные вопросы. При обсуждении вопросов, составленных учениками, учителю нужно искать возможности обратить внимание учащихся на ключевые моменты, направлять их более широкое рассмотрение вопроса.

Группам предлагаются задания по разным темам раздела. Цель работы учащихся на данном этапе – рассмотрение основных видов практических навыков, которыми они овладели при изучении раздела. Предполагается, что учащиеся будут самостоятельно изучать решения других групп. Поэтому постеры должны содержать последовательные подробные решения. Следует организовать отдельный обход постеров в каждой тройке групп с тремя разными заданиями. Однако можно организовать фронтальное обсуждение задач.

В конце урока учащимся предлагается задание олимпиадного характера, решение которого основано на применении свойств квадратичной функции.

Ответы и решения

Задания для групп

1) Движущаяся машина испытывает не только сопротивление воздуха, но и сопротивление дороги. Сопротивление f дороги движению автомобиля при скорости v км/ч выражается следующими формулами:

на хорошем шоссе ,

на плохом шоссе  .

Определите:

а) скорость движения на хорошем шоссе, при которой сопротивление должно быть наименьшим и величину этого наименьшего сопротивления.

б) при какой скорости сопротивление получается одинаковым как на плохом, так и на хорошем шоссе?

Решение.

а) Так как старший коэффициент квадратичной функции  положителен, то наименьшее значение функции достигается в вершине параболы.

, .

Значит, при скорости 10 км/ч сопротивление дороги будет минимальным, и будет равным .

б)

При скорости около 39 км/ч сопротивление получается одинаковым как на плохом, так и на хорошем шоссе.

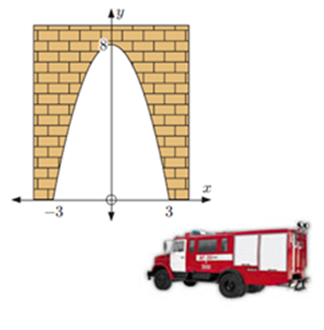
3) На рисунке показан туннель параболической формы (единицы измерения выражены в метрах).

а) Найдите квадратичную функцию, описывающую форму туннеля.

б) Пожарная машина имеет габаритные размеры 7400×2500×2800 мм (длина × ширина × высота). Определите, пройдет ли машина через туннель.

Решение.

а)

Точка (0; 8) принадлежит графику, значит , отсюда, .

б) 2500 мм = 2,5 м.

,

значит машина проедет через туннель.

Дополнительные разноуровневые задания

Уровень С

Сколько корней имеет уравнение:

(х – 2017)(х – 2018) + (х – 2018)(х – 2019) + (х – 2019)(х – 2017)=0?

Список полезных ссылок и литературы

1. Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Феоктистов И.Е. Алгебра. 9 класс : учеб. для учащихся общеобразоват. учреждений.  – М.: Мнемозина, 2010

2.  «Кенгуру» - выпускникам 9 класса. Тест готовности к продолжению образования.

3. Курбанов К.О. Некоторые прикладные задачи по высшей математике (методическое пособие). – Махачкала: Махачкалинский филиал МАДГТУ, 2011 г. – 24стр.

4. Эверстова Т.Л. Комплекс задач практического содержания как средство повышение интереса учащихся 9 класса к изучению математики (на примере темы «Квадратичная функция») (Ссылка на статью https://sibac.info/studconf/hum/xxvii/40129)

Скачано с www.znanio.ru