Вариант ВПР (собранный) 7 кл

1. Таблица содержит данные о пульсе бегунов-марафонцев.

А) Определите явно ошибочное значение (выброс), внесённое в эту таблицу.

Б) Удалите выброс и найдите наибольшее и наименьшее среди оставшихся значений.

В) Удалите выброс и найдите размах среди оставшихся значений.

Г) Удалите выброс и найдите среднее арифметическое среди оставшихся значений.

2.  Найдите значение выражения −4,5 + 6,24 : 1,6.

3.  Решите уравнение: 7 − 3(5x − 3)  =  −11x.

4.  Отметьте на числовой прямой точку  

5. Кофеварку на распродаже уценили на 20%, при этом она стала стоить 4800 рублей. Сколько рублей стоила кофеварка до распродажи?

6. На метеорологической станции города N в течение года наблюдали за температурой воздуха. По результатам наблюдений метеорологи построили график годового хода температуры.  В каком месяце была достигнута максимальная температура? В ответ запишите название месяца в именительном падеже.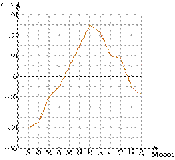

Найдите отношение числа месяцев с положительной температурой воздуха к числу месяцев с отрицательной температурой воздуха.

7.  Трактор едет по дороге, проезжая 10 метров за каждую секунду. Выразите скорость трактора в километрах в час. В ответе укажите число.

8.  В классе 25 учащихся. 9 из них после школы ходят в спортивную секцию, а 11 человек посещают музыкальную школу. Выберите верные утверждения и запишите в ответе их номера.

^{1)  Каждый учащийся, который посещает музыкальную школу, ходит в спортивную секцию.}

^{2)  Найдётся 5 учащихся, которые не ходят в спортивную секцию и не посещают музыкальную школу.}

^{3)  Меньше 10 учащихся и ходят в спортивную секцию, и посещают музыкальную школу.}

^{4)  Найдётся 10 учащихся, которые и ходят в спортивную секцию, и посещают музыкальную школу.}

9.  Чтобы приготовить рагу берут картофель, говядину и овощи в отношении 3 : 3 : 8. Известно, что повар заготовил 720 г говядины. Найдите суммарную массу (в граммах) картофеля и овощей.

ГЕОМЕТРИЯ

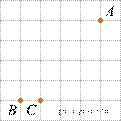
1.   На клетчатой бумаге с размером клетки 1 см × 1 см отмечены три точки: A, B и C. Найдите расстояние от точки A до прямой BC.

2. Углы, отмеченные на рисунке одной дугой, равны. Найдите угол α. Ответ дайте в градусах.

А) 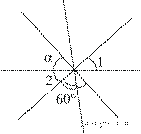  Б)

3. На клетчатой бумаге с размером клетки 1 × 1 нарисован треугольник ABC. Отрезок AM  — медиана данного треугольника. Найдите длину отрезка BM.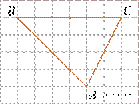

4.  Два внешних угла треугольника при разных вершинах равны. Периметр треугольника равен 78 см, а одна из сторон равна 18 см. Найдите две другие стороны треугольника. Ответ запишите в виде двух чисел, идущих подряд, без лишних знаков.

5.  Какое наименьшее число рёбер придется пройти дважды, чтобы обойти все рёбра куба и вернуться в исходную вершину?

6.  Высоты, проведенные к боковым сторонам АВ и АС остроугольного равнобедренного треугольника АВС, пересекаются в точке М. Найдите углы треугольника, если угол ВМС равен 140°.

1.  Найдите значение выражения −4,5 + 6,24 : 1,6.

Решение. Вычислим:

−4,5 + 6,24 : 1,6 = −4,5 + 3,9  =  −0,6.

Ответ: −0,6.

Таблица содержит данные о пульсе бегунов-марафонцев.

2.  Определите явно ошибочное значение (выброс), внесённое в эту таблицу.

Решение. Выбросом являются данные о пульсе Левицкого  — 14 уд/мин.

Ответ: 14.

3.  Удалите выброс и найдите наибольшее среди оставшихся значений.

Решение. Наибольшее значение среди всех измерений  — это 148 уд/мин.

Ответ: 148.

4.  Трактор едет по дороге, проезжая 10 метров за каждую секунду. Выразите скорость трактора в километрах в час. В ответе укажите число.

Решение. Трактор двигается со скоростью 10 м/с. Выразим эту скорость в километрах в час: км/ч.

Ответ: 36.

5.  В классе 25 учащихся. 9 из них после школы ходят в спортивную секцию, а 11 человек посещают музыкальную школу. Выберите верные утверждения и запишите в ответе их номера.

1)  Каждый учащийся, который посещает музыкальную школу, ходит в спортивную секцию.

2)  Найдётся 5 учащихся, которые не ходят в спортивную секцию и не посещают музыкальную школу.

3)  Меньше 10 учащихся и ходят в спортивную секцию, и посещают музыкальную школу.

4)  Найдётся 10 учащихся, которые и ходят в спортивную секцию, и посещают музыкальную школу.

Решение. 1)  Неверно, поскольку музыкальную школу посещают 11 человек, а спортивную секцию  — только 9 человек.

2)  Верно, поскольку если музыкальную школу и спортивную секцию посещают разные учащиеся, останется ещё 5 человек, которые никуда не ходят.

3)  Верно, поскольку наибольшее количество человек, которые могли бы ходить и в музыкальную школу, и в спортивную секцию  — 9.

4)  Неверно, поскольку музыкальную школу посещают 11 человек, а спортивную секцию  — только 9 человек.

Ответ: 23.

6.  Решите уравнение: 7 − 3(5x − 3)  =  −11x.

Решение. Найдем корень уравнения:

Ответ: 4.

7.  Отметьте на числовой прямой точку

Решение. Подпишем на координатной прямой точку A:

8. 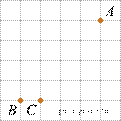 На клетчатой бумаге с размером клетки 1 см × 1 см отмечены три точки: A, B и C. Найдите расстояние от точки A до прямой BC.

Решение. Расстояние от точки до прямой равно длине перпендикуляра, опущенного из этой точки на прямую. По рисунку определяем это расстояние, оно равно четырем клеткам, или 4 см.

Ответ: 4.

9.  Два внешних угла треугольника при разных вершинах равны. Периметр треугольника равен 78 см, а одна из сторон равна 18 см. Найдите две другие стороны треугольника. Ответ запишите в виде двух чисел, идущих подряд, без лишних знаков.

Решение. 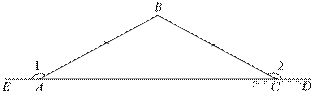Так как два внешних угла треугольника при разных вершинах равны, следовательно, треугольник ABC равнобедренный.

Если AC  =  18 см, то остальные стороны по (78 − 18) : 2  =  30 см.

Если AB  =  BC  =  18 см, то основание равно 78 − 2 · 18  =  42 см. Но такого треугольника не может существовать. Значит, второе предположение неверно.

Ответ: 30 см, 30 см.

На метеорологической станции города N в течение года наблюдали за температурой воздуха. По результатам наблюдений метеорологи построили график годового хода температуры.

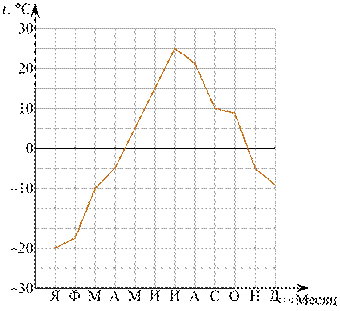
10.  В каком месяце была достигнута максимальная температура? В ответ запишите название месяца в именительном падеже.

Решение. По графику видно, что максимальная температура была достигнута в июле.

Ответ: июль.

11.  Найдите отношение числа месяцев с положительной температурой воздуха к числу месяцев с отрицательной температурой воздуха.

Решение. Из графика видно, что месяцев с положительной температурой воздуха всего 6  — май, июнь, июль, август, сентябрь и октябрь. Следовательно, месяцев с отрицательной температурой 12 – 6  =  6. Значит, искомое отношение  — 1 : 1.

Ответ: 1:1.

12.  Найдите значение выражения при и

Решение. Упростим выражение:

Подставим исходные данные и найдем значение выражения:

Ответ: −0,3.

13. 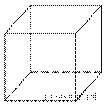 Какое наименьшее число рёбер придется пройти дважды, чтобы обойти все рёбра куба и вернуться в исходную вершину?

Решение. Нетрудно придумать обход, в котором дважды проходятся только четыре ребра. Докажем, что это минимальное количество.

При обходе необходимо выйти из начальной вершины, войти и выйти изо всех остальных вершины, затем вернуться в начальную вершину. Следовательно, каждая вершина будет пройдена четное число раз. В вершинах сходятся по три ребра, поэтому входов-выходов должно быть не менее четырех. У куба 8 вершин, значит, всего должно быть не менее 32  проходов вершин. Каждой паре выход-вход соответствует одно ребро, а потому необходимо не менее 16 проходам по ребрам. Куб имеет 12  ребер. Поэтому пройдены дважды будут минимум 4  ребра.

Ответ: 4.

14.  Решите систему уравнений

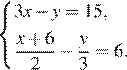
Решение. Выразим y из первого уравнения и подставим во второе, предварительно умножив обе его части на 6:

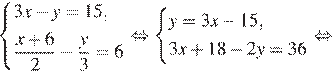
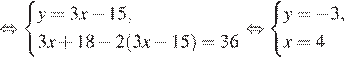
Ответ: (4; −3).

15.  Кофеварку на распродаже уценили на 20%, при этом она стала стоить 4800 рублей. Сколько рублей стоила кофеварка до распродажи?

Решение. Кофеварку ценили на 20%, таким образом, полученная сумма составляет 100% − 20%  =  80%. Тогда до распродажи курка стоила 4800 : 0,8  =  6000.

Ответ: 6000.

16.  

Прямые m и n параллельны. Найдите ∠3, если ∠1= 38°, ∠2 = 76°. Ответ дайте в градусах.

Решение.

Введем обозначение, как показано на рисунке. Углы 1 и 4 соответственные, поэтому ∠4  =  ∠1  =   38°. Углы 2, 3 и 4  — это углы одного треугольника, сумма углов треугольника равна 180°, откуда ∠3  =  180° − 38° − 76°  =  66°.

Ответ: 66.

17.  Чтобы приготовить рагу берут картофель, говядину и овощи в отношении 3 : 3 : 8. Известно, что повар заготовил 720 г говядины. Найдите суммарную массу (в граммах) картофеля и овощей.

Решение. Из пропорции очевидно равенство масс картофеля и говядины, значит, картофеля так же 720 г. Найдем массу овощей:

Итак, суммарно картофель и овощи имеют массу 720 + 1920  =  2640 г.

Ответ: 2640 грамм.

18.  Высоты, проведенные к боковым сторонам АВ и АС остроугольного равнобедренного треугольника АВС, пересекаются в точке М. Найдите углы треугольника, если угол ВМС равен 140°.

Решение. 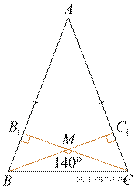По свойству смежных углов угол CMB₁ равен 180° − 140°  =  40°. Следовательно, угол MCA равен 90° − 40°  =  50°. Угол  A равен 90° − 50°  =  40°. По свойству углов в равнобедренном треугольнике углы B и С равны (180° − 40°) : 2  =  70°.

Ответ: 40°, 70°, 70°.

19.  Найдите две последние цифры числа 82**, если оно делится на 90.

Решение. Чтобы число делилось на 90, оно должно делится на 9 и на 10. Поставим в конец числа 0, оно будет делится на 10. Чтобы обеспечить делимость на 9, подберем предпоследнюю цифру так, чтобы сумма цифр числа делилась на 9. Подойдет цифра 8: 8 + 2 + 8 + 0  =  18. Получаем: 8280.

Ответ: 8280.