
Векторы и
матрицы. Переменной может быть присвоено значение матрицы (вектор-столбец —
это матрица с одним столбцом). Для этого используем палитру векторов и матриц
Просмотр\Панели\Матрица ![]() . Например, перменная М — есть матрица
размером 3х3, а переменная N — вектор-столбец размером
3x1:
. Например, перменная М — есть матрица
размером 3х3, а переменная N — вектор-столбец размером
3x1:
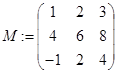 ,
, 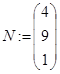 .
.
MathCad позволяет выполнить все допустимые операции с матрицами. Например, обратную матрицу получаем, указав (–1) степень, а операцию транспонирования выбираем из палитры векторов и матриц.
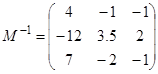 ,
, 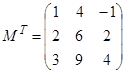
Можно решить систему уравнений матричным способом, в нашем случае:
![]()
Доступ к элементу матрицы производится по индексу, отсчитываему от 0. Вектор-столбец имеет один индекс, который вводится при помощи символа левой квадратной скобки «[» или с помощью панели «Калькулятор».
Например, значения компонентов вектора N можно вывести так:
![]()
![]()
![]()
![]() .
.
Для этого вводится N[0= N[1= N[2=.
Двумерный массив имеет уже два индекса, также отсчитываемые от 0, первый из них нумерует строки, второй — столбцы. Так, для матрицы M имеем:
![]()
![]()
![]() .
.
Для этого вводится М[0,0= М[0,1= М[1,0= Индексы разделяются запятыми.
Можно выбрать один столбец
двумерного массива, вводя верхний индекс командой Ctrl+6 или кнопкой ![]() палитры
векторов и матриц.
палитры
векторов и матриц.
Легко
вычислить скалярное (Shift 8) ![]() и векторное (Ctrl 8)
и векторное (Ctrl 8) ![]() произведения
векторов соответственно:
произведения
векторов соответственно:
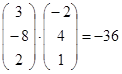
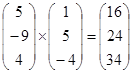 .
.
Поэлементные вычисления над матрицами выполняются с помощью операции векторизации (вводится комбинацией клавиш «Ctrl–» или кнопкой панели Матрица). При её использовании операции производятся над каждым элементом вектора независимо:
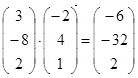 .
.
В следующем примере с помощью векторизации получаем решения квадратного уравнения для нескольких исходных данных:
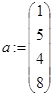 ,
, 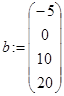 ,
,
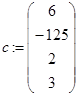
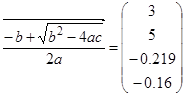
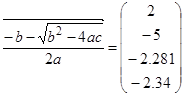
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.