Вопрос 35.doc

Погрешность вычислений, обусловленность, структура погрешности.

При решении задач необходимо найти функции, описывающие процессы, которые удовлетворяют системе дифф. или интегр. уравнений и некоторым условиям (реже функции удовлетворяют алгебраической системе уравнений). Точное аналитическое решение этих дифф. и интегр. уравнений сводится к нахождению элементарной или специальной функции. Эти методы либо беспомощны либо их использование связано с недопустимыми затратами усилий и времени. Поэтому, для решения задач используют приближенные методы, которые делят на три группы. 1) аналитические, применение дает решение дифф., интегр. или алгебр. уравнения  в виде аналитического выражения (ряда, функции, полинома).  2)графические методы, дают приближенные решения в виде графика или поверхности. 3) численные методы – искомая функция получается в виде таблицы чисел. При численном решении дифф. и интегр. уравнений получаются значения искомой функции, найденные с какой-то точностью (с точностью до заданного числа). Источники возникновения погрешностей. 1) математическое описание задачи является неточным, т.е. неточно заданы исходные данные описание задачи, – неустранимая погрешность; 2) применяемый для решения задачи метод не является точным – погрешность метода; 3) при вводе данных  в компьютер, при вычислении арифметических операций, при выводе данных производится округление – вычислительная погрешность.

Формальное определение погрешности. Обозначим J – точное (недостижимое) решение заданной задачи, – значение параметра, соответствующее принятой матем. модели,  – численно найденное выбранным методом решения задачи без округления,  – приближенное решение задачи, полученное при реальных вычислениях. r₁₌–J – неустранимая погрешность (погрешность модели); – погрешность метода; – вычислительная погрешность; – полная погрешность, т.е. .

Приближенные числа, их абсолютные и относительные погрешности. Разумная оценка погрешности при вычислениях позволяет указать оптимальное количество знаков, которое следует сохранять при расчетах, а также окончательных результатах. Погрешностью приближенного числа a называется разность a–a₀, где a– приближенное значение, a₀– точное значение, которое не известно. Под оценкой погрешности приближенного числа a понимают установление неравенства  (1), где  - абсолютная погрешность приближенного числа a; на практике стараются указать меньшее число , удовлетворяющее неравенству (1). Абсолютную погрешность записывают с двумя, тремя значащими цифрами (при подсчете числа значащих цифр не учитываются нули, стоящие слева от записи числа). В приближенном числе a не следует сохранять те разряды, которые подвергаются округлению в его абсолютной погрешности. Относительная погрешность  обозначается ,  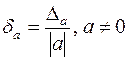(2). Выражается в процентах, т.е. *100%, ее необходимо записывать не более чем с двумя-тремя значащими цифрами.