Вопрос 36.doc

Постановка задачи интерполяции.

Пусть известные значения функции f образуют таблицу:

…(*)

Найдем значения функции f для аргумента x, такого что , т.е. не совпадает ни с одним значением из таблицы. Т.е. задача заключается в том, чтобы по исходной таблице построить приближенную функцию F, которая близка к f, то есть F: f(x)=F(x) (1). Требуется, чтобы функции совпадали точно для x_i, где i=, т.е. F(x₀)=y₀,…, F(x_n)=y_n (2).

Процесс нахождения F, которая ведет себя согласно формулам (2), называется интерполяцией, а точки x₀ , x₁…x_n  называются узлами интерполирования. Самый простой способ поиска  F будет, если записать функцию F в виде полинома . Этот многочлен  содержит n+1 коэффициентов и n+1 условий (2), т.е. условия (2) позволяют однозначно определить коэффициенты уравнения (a_{0 ,}a₁…a_n).  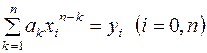(3), i - номер уравнения, k – номер неизвестного. Выпишем определитель системы (полагая, что все x_i различны):

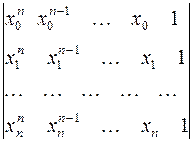  ¹0, он называется определителем Вандермонда.                                                                                 

Вывод: интерполяционный многочлен  (3) для функции f, которая задается таблицей, существует и он единственный.

Утверждение: Интерполяционный полином P_n(x) имеет степень, не большую, чем n.      

Интерполяционный многочлен Лагранжа.

Пусть функция f задана значениями y₀ , y₁,…, y_n  в соответствующих точках x₀, x₁ ,…, x_n. Построим интерполяционный многочлен L_n(x), степень которого не больше n и для которого выполняется условие :F(x₀)=y₀, F(x₁)=y₁, …, F(x_n)=y_n (1), где приближенно f(x)=F(x). Будем искать L_n(x) в виде: L_n(x)=l₀(x)+l₁(x)+…+l_n(x)  (2), где  l_i(x) – многочлен степени n, причем l_i(x_k)=y_i, если i=k и l_i(x_k)=0, если   (3). Очевидно, что требование (3) с учетом (2) обеспечивает выполнение условий (1). Многочлены  l_i(x) составим следующим образом: l_i(x)=c_i(x–x₀)(x–x₁)…(x–x_i–1)(x–x_i+1)…(x–x_n) (4), где c_i – постоянный коэффициент, значение которого найдем из первой части условия (3): 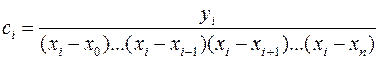, при  этом ни один множитель в знаменателе не равен  нулю. Подставим  c_i  в (4) с учетом (2), получим: .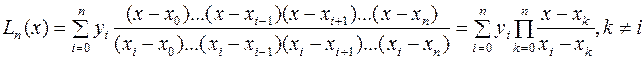

Оценка  погрешности  интерполяции.

Если известно аналитическое выражение интерполируемой функции f, то можно применить формулы для оценки погрешности интерполирования (погрешность метода). Остаточный член интерполируемого многочлена имеет вид: R_n(x)=f(x)-g_n(x)

В силу единственности интерполируемого многочлена формула оценки погрешности используется и для многочлена Лагранжа и для многочлена Ньютона. Предположим, что f(x) имеет все производные до n+1 порядка, т.е. f⁽ⁿ⁺¹⁾(x). Введем вспомогательную функцию u(x)=f(x)-g_n(x)-k*W_n+1(x)  (1), она имеет n+1 корней, это узлы интерполяции (x₀, x₁,..., x_n). W_n+1(x)=(x-x₀)(x-x₁)…(x-x_n), k выбирается из условия u(x*)=0, где x*–точка в которой оценивается погрешность, x*x_i, i=.

Из u(x*)=0 получаем: 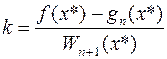. При таком выборе k функция u(x) обращается в ноль в (n+2) точках: x₀, x₁,…, x_n, x*.

Воспользуемся теоремой Ролля. Теорема Ролля: пусть функция f(x) непрерывна на отрезке [a,b] и дифференцируема на интервале (a,b). Если f(a)=f(b), то найдется, по крайней мере, одна точка , в которой . По т.Ролля производная обращается в ноль, по крайней мере, в n+1 точках. Применяя т.Ролля к функции , получим, что  обращается в ноль в n точках. Продолжая рассуждения, получим, что u⁽ⁿ⁺¹⁾(x) обращается в ноль, по крайней мере, в 1 точке принадлежащей отрезку [y₁,y₂].

, y₁=min(x₀, x₁,…, x_n, x*), y₂=max(x₀, x₁,…, x_n, x*).

Т.к. u⁽ⁿ⁺¹⁾(x)=f⁽ⁿ⁺¹⁾(x)–k(n+1)! , то из условия: u⁽ⁿ⁺¹⁾()=0 получаем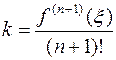

Соотношение u(x)=0  перепишем в виде: f(x)–g_n(x)=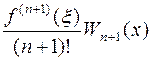, где .

Если принять , (x₀xx_n), то 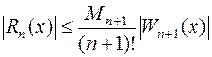– оценочная формула, применяемая для подсчета погрешности методом интерполяции по формуле Лагранжа.