
Вычисление определенных интегралов по квадратурным формулам Ньютона–Котеса, формулам прямоугольников и трапеций, их погрешность.
Формулы, используемые для приближенного вычисления однократных интегралов, называются квадратурными формулами (квадратурами).
Самый простой способ построения квадратур:
подынтегральная функция f(x) на [a;b]
заменяется интерполяционным многочленом Ln(x). 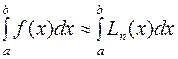 .
. 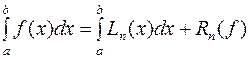 ,
где Rn(f)–остаточный
член квадратурных формул. При этом отрезок [a;b] разбивается точками на n
частей: a=x0, x1, x2,…, xn=b или
узлами, которые подразумеваются при построении Ln(x). Подставив
выражение для Ln(x), получим:
,
где Rn(f)–остаточный
член квадратурных формул. При этом отрезок [a;b] разбивается точками на n
частей: a=x0, x1, x2,…, xn=b или
узлами, которые подразумеваются при построении Ln(x). Подставив
выражение для Ln(x), получим: 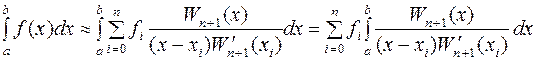 ,Wn+1(x)=(x–x0)(x–x1) …(x–xn) Т.о.
,Wn+1(x)=(x–x0)(x–x1) …(x–xn) Т.о. 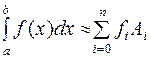 , где
, где 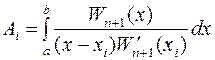
Разобьем отрезок интегрирования [a;b] на
n равных частей системой точек xi=x0+ih,
i=![]() , x0=a,
xn=b, h=(b–a)/n.
Преобразуем выражение Wn+1(x)=(x-x0)(x-x1)…(x-xn) (1).
Введем подстановку t=(x–x0)/h
=>x–x0=ht,
x–x1=x–(x0+h)=h(t–1), x–x2=x–(x0+2h)=h(t–2),…, x–xi=h(t–i)
, x0=a,
xn=b, h=(b–a)/n.
Преобразуем выражение Wn+1(x)=(x-x0)(x-x1)…(x-xn) (1).
Введем подстановку t=(x–x0)/h
=>x–x0=ht,
x–x1=x–(x0+h)=h(t–1), x–x2=x–(x0+2h)=h(t–2),…, x–xi=h(t–i)
Подставим эти разности в (1), получим: Wn+1(x)=hn+1 t(t+1)…(t–n)
Т.к. xi–x0=hi, xi–x1=h(i–1),…, xi–xn=h(n–i), то W’n+1(xi)=(xi–x0)...(xi–xi–1)( xi–xi+1)… ( xi–xn) =hn i(i–1)...1(–1)...(–(n–i))=hn i!(n–i)!(–1)n–i
Подставим полученные значения в Ai, тогда: 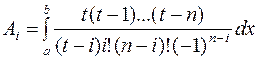
Перейдем к переменной t: x–x0=ht => dx=h dt=(b–a)dt/n
При x=x0 t=0, x=xn t=n; 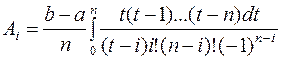
Числа
Ai называются коэффициентами Котеса, они не зависят от f(x), а зависят от числа n. Формулы
Ньютона–Котеса: 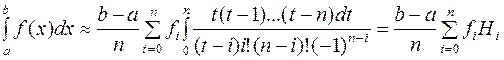
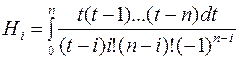
Пусть в точке (b+a)/2 известно значение функции f(x), т.е. f((b+a)/2)
Тогда формула прямоугольника имеет вид: 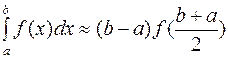 с оценкой остаточного члена
с оценкой остаточного члена 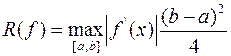 . Обобщенная формула
прямоугольников с левыми ординатами:
. Обобщенная формула
прямоугольников с левыми ординатами: 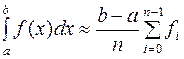 , с правыми
ординатами:
, с правыми
ординатами: 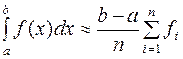
Абсолютную погрешность формулы прямоугольников можно
оценить по формуле 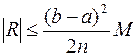 , где
, где ![]()
При
n=1,i=0,1из формул Ньютона–Котеса 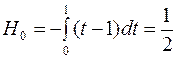 ,
,
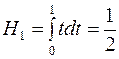 Подставим H1, H0 в формулы
Ньютона–Котеса:
Подставим H1, H0 в формулы
Ньютона–Котеса: 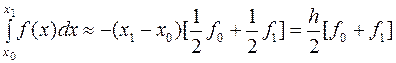
Распространяя
последнюю формулу на все отрезки разбиения, получим обобщенную формулу
трапеций для отрезка [a,b]: 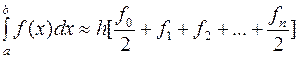 Оценим
погрешность интегрирования по формуле трапеций. Вначале получим формулу
остаточного члена для отрезка [x0,x1]:
Оценим
погрешность интегрирования по формуле трапеций. Вначале получим формулу
остаточного члена для отрезка [x0,x1]: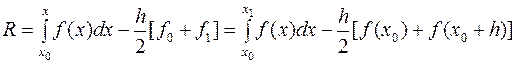 ; R=R(h), R(0)=0
; R=R(h), R(0)=0
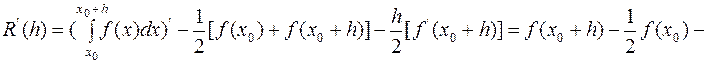
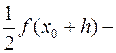
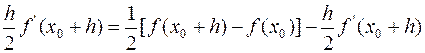 Должно
выполнятся R’(0)=0
Должно
выполнятся R’(0)=0 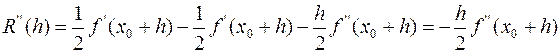
Определим R, последовательно интегрируя R’’(x) на отрезке [0,h]
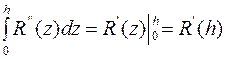 Из двух последних равенств
получаем (вместо h z):
Из двух последних равенств
получаем (вместо h z):
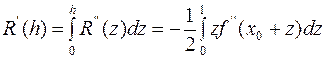 Применяя
теорему о среднем, получим:
Применяя
теорему о среднем, получим:
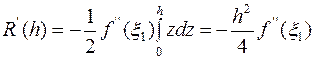 ,
, ![]() ,
,
![]() зависит от h.
зависит от h.
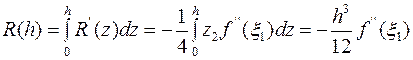 ,
, ![]()
Т.о.
погрешность метода интегрирования по формуле трапеций на отрезке [x0,x1] имеет величину
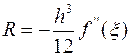 , где
, где ![]() ;
;
на
[a,b] 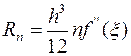 ,
, 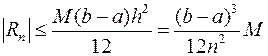 , где
, где ![]() . При
. При ![]() >0 формула
дает приближение с избытком, при
>0 формула
дает приближение с избытком, при ![]() <0 с
недостатком.
<0 с
недостатком.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.