Вопрос 49.doc

Позиционные системы счисления.

Способ представления числа определяется системой счисления. [ Система счисления - это правило записи чисел с помощью заданного набора специальных знаков - цифр.

Людьми использовались различные способы записи чисел, которые можно объединить в несколько групп: унарная, непозиционные и позиционные.

Унарная - это система счисления, в которой для записи чисел используется только один знак - I («палочка»). Следующее число получается из предыдущего добавлением новой I; их количество (сумма) равно самому числу.

Из непозиционных наиболее распространенной можно считать римскую систему счисления. В ней некоторые базовые числа обозначены заглавными латинскими буквами: 1 -1, 5- V, 10-Х, 50-L ,100 - С, 500 - D, 1000 - М. Все другие числа строятся комбинаций базовых в соответствии со следующими правилами:

• если цифра меньшего значения стоит справа от большей цифры, то их значения суммируются; если слева - то меньшее значение вычитается из большего.

• цифры /, X, С и М могут следовать подряд не более трех раз каждая;

• цифры V, L и D могут использоваться в записи числа не более одного раза.

Например, запись XIX соответствует числу 19, MDXLIX – числу 1549.

В настоящее время для представления чисел применяют, в основном, позиционные системы счисления.

Позиционными называются системы счисления, в которых значение каждой цифры в изображении числа определяется ее положением (позицией) в ряду других цифр.

Наиболее распространенной и привычной является система счисления, в которой для записи чисел используется 10 цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9. Число представляет собой краткую запись многочлена, в который входят степени некоторого другого числа - основания системы счисления.

По принципу, положенному в основу десятичной системы счисления, очевидно, можно построить системы с иным основанием. Пусть р - основание системы счисления. Тогда любое число Z (пока ограничимся только целыми числами), удовлетворяющее условию Z <  (k > 0, целое), может быть представлено в виде многочлена со степенями р (при этом, очевидно, максимальный показатель степени будет равен k-1):

Индекс р у числа Z указывает, что оно записано в системе счисления с основанием р; общее число цифр числа равно k. Все коэффициенты аj- целые числа, удовлетворяющие условию: 0<аj<р-1.

Система счисления с основанием 2 называется двоичной. Цифрами двоичной системы являются 0 и 1, а форма строится по степеням 2. Интерес именно к этой системе счисления связан с тем, что, как указывалось выше, любая информация в компьютерах представляется с помощью двух состояний - 0 и 1, которые легко реализуются технически. Наряду с двоичной в компьютерах используются 8-ричная и 16-ричная системы счисления - причины будут рассмотрены далее. Необходимо еще раз подчеркнуть, что значение целого числа, т.е. общее количество входящих в него единиц, не зависит от способа его представления и остается одинаковым во всех системах счисления; различаются только формы представления одного и того же количественного содержания числа.

Преобразование целых чисел из одной системы счисления в другую.

Преобразование Zp –>Z1—> Xq

Идея алгоритма перевода предельно проста: положим начальное значение Zq:= 0; из числа Zp вычтем 1 по правилам вычитания системы р, т.е. Zp:=Zp- и добавим ее к Zq по правилам сложения системы q, т.е. Zq:= Zq+ 1; будем повторять эту последовательность действий, пока не достигнем Zp = 0.

Правила сложения с 1 и вычитания 1 могут быть записаны следующим образом:

Для системы р             Для системы q

(р-1)-1=(р-2)                 0 + 1 = 1

(р-2)-1=(р-3)                 1 + 1=2

…….                    ……

1 -1 =0                           (q-2)+1=q-1

0-1=(p-1)             (q-1)+1=0

Преобразование Zp —> Z10 —>Zq

Промежуточный переход к унарной системе счисления в дан­ном случае осуществляется неявно - используется упоминавшее­ся выше свойство независимости значения числа от формы его представления. Рассмотренный алгоритм перевода может быть легко реализован программным путем, в частности, машиной Тью­ринга.

Очевидно, первая и вторая часть преобразования не связаны друг с другом, что дает основание рассматривать их по отдельности. Алгоритмы перевода Z10 —> Zq вытекают из следующих сообрaжений. Многочлен для Zq может быть представлен в виде:

где т - число разрядов в записи Zq, а bj (j = 0...m - 1) – цифры числа Zq.

Возможны 2 способа перевода:

Способ №1 алгоритм перевода:

1) целочисленно разделить исходное число (Z10) на основание новой системы счисления (q) и найти остаток от деления - это будет цифра 0-го разряда числа Zq;

2) частное от деления снова целочисленно разделить на Q с выделением остатка; процедуру продолжать до тех пор, пока частное от деления не окажется меньше q;

3) образовавшиеся остатки от деления, поставленные в порядке, обратном порядку их получения, и представляют Zq.(деление столбиком)

Способ №2 алгоритм перевода:

1)     определить т - 1 - максимальный показатель степени в представления числа по форме для основания q;

2)    целочисленно   разделить   исходное число (Z10) на основание новой системы счисления в степени т -1 (т.е.) и найти остаток отделения; результат деления определит первую цифру числа Z;

3)     остаток от деления целочисленно разделить на , результат деления принять за вторую цифру нового числа; найти остаток; продолжать эту последовательность действий, пока показатель степени q не достигнет значения 0.

Алгоритм Zp->Z10  явно вытекает из 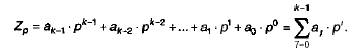 и  . Необходимо  Zp представить в форме многочлена и выполнить все операции по правилам десятичной арифметики.

Пример: Выполнить преобразование 443₅ -> Z₁₀

443₅ = 4*5²+ 4*5¹ + 3-5° = 4*25 + 4*5 + 3*1 = 123₁₀

Представление дробей в различных системах счисления и их преобразование.

Вещественное число, в общем случае содержащее целую и дробную часть, всегда можно представить в виде суммы целого числа и правильной дроби. Поскольку проблема записи натуральных чисел в различных системах счисления уже была решена, можно ограничить рассмотрение только алгоритмами перевода правильных дробей. Введем следующие обозначения: правильную дробь в исходной системе счисления р будем записывать в виде 0,Yp, дробь в системе q - 0,Yq, а преобразование - в виде 0,Уp-> Q,Yq. Последовательность рассуждений весьма напоминает проведенную ранее для натуральных чисел. В частности, это касается рекомендации осуществлять преобразование через промежуточный переход к 10-ной системе, чтобы избежать необходимости производить вычисления в «непривычных» системах счисления, т.е. 0,Уp -> 0,У10 -> 0,Yq. Это, в свою очередь, разбивает задачу на две составляющие: преобразование 0, Ур-> 0, У10 и 0, У10-> 0, Yq, каждое из которых может рассматриваться независимо.

Алгоритмы перевода 0.У10–> 0,Yq выводится путем следующих рассуждений. Если основание системы счисления q, простая дробь содержит п цифр и bk- цифры дроби (1 <=k<=n, 0 < bk < q -1), то она может быть представлена в виде суммы:

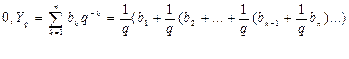
алгоритм преобразования

1) умножить исходную дробь в 10-ной системе счисления на q, выделить целую часть - она будет первой цифрой новой дроби; отбросить целую часть;

2) для оставшейся дробной части операцию умножения с выделением целой и дробных частей повторять, пока в дробной части не окажется 0 или не будет достигнута желаемая точность конечного числа (exact)', появляющиеся при этом целые будут цифрами новой дроби;

3) записать дробь в виде последовательности цифр после ноля с разделителем в порядке их появления в п. (1) и (2).

Пример Выполнить преобразование 0,375₁₀ —> О,Y2

Таким образом, 0,37510 - 0,011₂.

Перевод 0,Ур->0,Y10 как и в случае натуральных чисел, сво­дится к вычислению значения формы в десятичной системе счисления.

Например,0,011₂ = 0*2 + 1*2^-2 + 1*2 = 0,25 + 0,125 = 0,3710.

Следует сознавать, что после пере­вода дроби, которая была конечной в исходной системе счисления, она может оказаться бесконечной в новой системе. Соответственно, рациональное число в исходной системе может после перехо­да превратиться в иррациональное. Справедливо и обратное утверждение: число иррациональное в исходной сис­теме счисления в иной системе может оказаться рациональным.

Правила преобразований целых чисел Z₂ ¬®Z₄ ¬® Z₁₆ .

Интерес к двоичной системе счисления вызван тем, что именно эта система используется для представления чисел в компьютере. Однако двоичная запись оказывается громоздкой, поскольку содержит много цифр, и, кроме того, она плохо воспринимается и запоминается человеком из-за зрительной однородности (все число состоит из нулей и единиц). Поэтому в нумерации ячеек памяти компьютера, записи кодов команд, нумерации регистров и устройств и пр. используются системы счисления с основаниями 8 и 16; выбор именно этих систем счисления обусловлен тем, что переход от них к двоичной системе и обратно осуществляется, как будет показано ниже, весьма простым образом.

Двоичная система счисления имеет основанием 2 и, соответственно, 2 цифры: 0 и 1.

Восьмеричная система счисления имеет основание 8 и цифры 0,1,. ..,7.

Шестнадцатеричная система счисления имеет основание 16 и цифры 0, 1, .... 9, А, В, С, D, Е, F. При этом знак «А» является 16-ричной цифрой, соответствующей числу 10 в десятичной системе; Б16 = 1110; С16 = 1210; D16 = 1310; Е16 = 1410; F16 = 1510. Другими словами, в данном случае А ... F- это не буквы латинского алфавита, а цифры 16-ричной системы счисления и поэтому они имеют только такое начертание (не могут быть представлены в виде, например, соответствующих строчных букв, как в текстах).

Докажем две теоремы.

Теорема 1. Для преобразования целого числа Zp — > Zq в том случае, если системы счисления связаны соотношением q = ,где r - целое число большее 1, достаточно Zp разбить справа налево на группы по r цифр и каждую из них независимо перевести в систему q.

Доказательство:

Пусть максимальный показатель степени в записи числа р равен k-1, причем, 2r> k-1 > r.

Таким образом, r-разрядные числа системы с основанием р оказываются записанными как цифры системы с основанием q. Этот результат можно обобщить на ситуацию произвольного k-1 >r - в этом случае выделится не две, а больше (t) цифр числа с основанием q. Очевидно, Zq = (bm ...b0)q

Теорема 2. Для преобразования целого числа Zp —> Zq в том случае, если системы счисления связаны соотношением р = , где r- целое число большее 1, достаточно каждую цифру Zp заменить соответствующим r-разрядным числом в системе счисления q, дополняя его при необходимости незначащими нулями слева до группы в г цифр.

Доказательство:

Пусть исходное число содержит две цифры, т.е.

Для каждой цифры справедливо: 0 < аи поскольку р = , 0 < а, то в представлении этих цифр в системе счисления q максимальная степень многочленов будет не более r- 1 и эти многочлены будут содержать по r цифр:

,

.

Тогда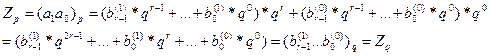

причем, число Z_q содержит 2r цифр. Доказательство легко обоб­щается на случай произвольного количества цифр в числе Z_Р.