Поделиться
ВОЗВЕДЕНИЕ В КВАДРАТ СУММЫ И РАЗНОСТИ2.docx
Возведение в
квадрат суммы и разности
двух выражений
Цели: продолжить формирование умения возводить в квадрат двучлен; преобразовывать выражения, используя соответствующие формулы; проверить уровень усвоения материала.
Ход урока
I. Устная работа.
Выполните возведение в квадрат.
а) (c + d)2; б) (x + 1)2; в) (a – 2)2; г) (y – 5)2.
II. Формирование умений и навыков.
Сначала необходимо разобрать, как возводить в квадрат выражения вида –a + b и –a – b. Затем перейти к упрощению выражений с использованием формул квадрата суммы и разности. В соответствии с этим задания делятся на две группы.
1-я группа
Сначала предложить учащимся преобразовать выражения (–x + 3)2
и (–y + 7)2. Согласно известным формулам преобразования будут
выглядеть следующим образом:
(–x + 3)2 = (–x)2 + 2 ∙ (–x) ∙ 3 + 32 = x2 – 6x + 9;
(–y + 7)2 = (–y)2 + 2 ∙ (–y) ∙ 7 + 72 = y2 – 14y + 49.
Учащиеся должны осознать, что в таком виде возведение в квадрат проводить неудобно, лучше поменять местами выражения:
(3 – x)2 = 32 – 2 ∙ 3 ∙ x + x2 = 9 – 6x + x2;
(7 – y)2 = 72 – 2 ∙ 7 ∙ y + y2 = 49 – 14x + y2.
Затем следует выполнить № 807. После этого сделать соответствующие выводы:
(–a + b)2 = (b – a)2;
(a – b)2 = (b – a)2;
(–a – b)2 = (a + b)2.
Нужно объяснить учащимся, что применение этих равенств упрощает возведение в квадрат двучлена и пригодится им при дальнейших преобразованиях выражений.
После этого можно перейти к выполнению заданий.
1. № 805, 806.
2. № 809.
Решение:
а) 
б) 
в) 
г)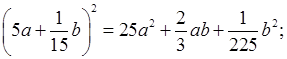 
д) 
е) 
2-я группа
1. № 815.
2. № 817 (а, в, д).
Решение:
а) 
в) 
д) 
= –2a2 + 4a + 14.
III. Проверочная работа.
Вариант 1
1. Преобразуйте в многочлен.
а) (у + 4)2; б) (2х – 3у)2; в) (–3а + 5)2; г) (–х2 – 2х)2.
2. Упростите выражение.
а) (8а – b)2 – 64а2; б) а (4 – а) + (4 – а)2.
Вариант 2
1. Преобразуйте в многочлен.
а) (х – 6)2; б) (7т + 3п)2; в) (–2у + 3)2; г) (–х3 – 4х)2.
2. Упростите выражение.
а) 81х2 – (9х + 2у)2; б) х (х – 7) + (х + 3)2.
IV. Итоги урока.
– Как возвести в квадрат сумму (разность) двух выражений?
– Как возвести в квадрат выражения вида –а + b и –а – b?
Домашнее задание: № 808; № 816; № 817 (б, г, е).
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.
