ВОЗВЕДЕНИЕ В КВАДРАТ СУММЫ И РАЗНОСТИ2

Возведение в квадрат  суммы и разности
двух выражений

Цели: вывести формулы квадрата суммы и разности двух выражений; формировать умение использовать эти формулы.

Ход урока

I. Устная работа.

1. Выполните возведение в степень.

а) (–2х)²;                        в) 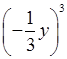;                         д) (–7х³у²)²;

б) (5а²)²;                        г) 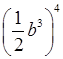;                          е) (–0,6п⁴т⁵)².

2. Выполните умножение.

а) 2х² · 3х⁷;                    в) 3а (2а² – 5а);                 д) (х – 3) (у + 4);

б) y⁵ · (–4y³);            г) –2x⁴ 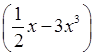;         е) (2a – 1) (b – 5).

II. Объяснение нового материала.

Объяснение нового материала следует производить в несколько этапов. 1.  представить выражение (a + b)² в виде многочлена.

(a + b)² = (a + b) (a + b) = a² + ab + ab + b² = a² + 2ab + b².

Аналогично возводится в квадрат выражение a – b:

(a – b)² = (a – b) (a – b) = a² – ab – ab + b² = a² – 2ab + b².

2 полученные тождества называются формулами квадрата суммы и разности двух выражений. Они нужны, чтобы сделать проще преобразования.

3. Разобрать примеры 1 и 2 из учебника. Остальные примеры приводить пока не нужно.

III. Формирование умений и навыков.

1. № 799.

2. № 803.

решение:

(Во избежание ошибок следует вести подробные записи.)

а) (2x + 3)² = (2x²) + 2 · 2x · 3 + 3² = 4x² + 12x + 9;

д)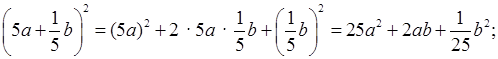

е)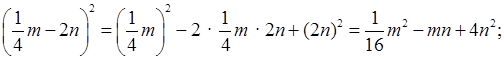

з) (10с + 0,1у)² = (10с)² + 2 · 10с · 0,1у + (0,1у)² = 100с² + 2су + 0,01у².

3. № 812.

Решение:

а) (а² – 3а)² = (а²)² – 2а² · 3а + (3а)² = а⁴ – 6а³ + 9а²;

б)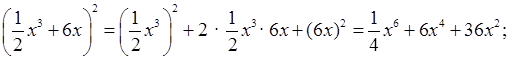

в)  = c⁴ – 1,4c⁵ + 0,49c⁶;

г)  = 16y⁶ – 4y⁵ +
+ 0,25y⁴;

д) 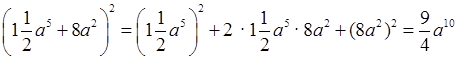 + 24a⁷ +
+ 64a⁴;

е) = 0,36b² – 72b³ +
+ 3600b⁴.

IV. Итоги урока.

– Как возвести в квадрат сумму двух выражений?

– Как возвести в квадрат разность двух выражений?

– Зачем нужны формулы квадрата суммы и разности двух выражений?

– Выполните возведение в квадрат:   а) (3а + 1)²;   б) (х – 5)².

Домашнее задание: № 800; № 804; № 813.