Вписанная и описанная окружность_Приложения4

Приложение 1

1.      Прямая CD серединный перпендикуляр отрезка AB докажите, что AC = BC.

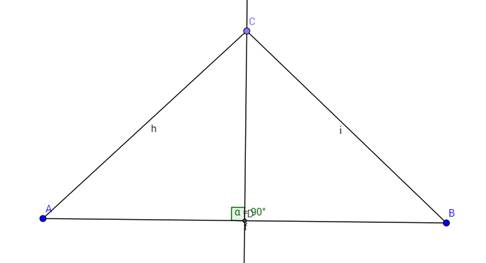
Делаем вывод: Любая точка, лежащая на серединном перпендикуляре ____________________ от концов отрезка.

2.      На отрезке AB длиной 6 см постройте серединный перпендикуляр. Отмерьте на нем 4 см отрезок CM, где M середина отрезка AB. Опытным путем установите длину отрезков AC и BC. (Задача на построение)

3.      Прямая AD биссектриса угла ABC. DE и DF высоты опущенные к прямым AB и AC соответственно. Докажите, что DE = DF.

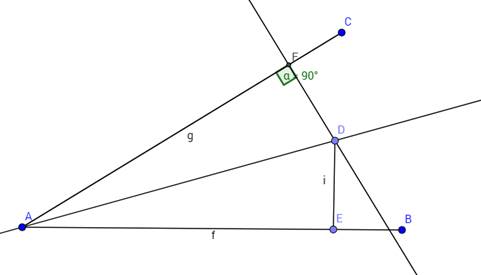
Делаем вывод: Любая точка, лежащая на биссектрисе угла равноудалена от ___________ этого угла.

4.   Проведите биссектрису угла CAB с угловой величиной в  ̊.  Отмерьте на биссектрисе отрезок AD длиной в 8 см. DE и DF высоты, опушенные с точки D на стороны угла. Чему равны длины отрезков DE и DF.

Приложение 2

Группа А

Постройте треугольник со сторонами 7 см и 5 см и с углом между ними в 70 ̊ и проведите серединные перпендикуляры с каждой стороны. Ответьте на вопросы:

a)      Пересекаются ли все серединные перпендикуляры в одной точке?

b)      Могу ли я построить окружность с центром в точке пересечения серединных перпендикуляров и проходящая через вершины треугольника?

c)       Как бы вы могли эту окружность назвать? (Определение 1)

Группа В

Постройте треугольник со сторонами 7 см и 5 см и с углом между ними в 70 ̊ и проведите биссектрису с каждого угла треугольника. Ответьте на вопросы:

a)      Пересекаются ли все биссектрисы в одной точке?

b)      Могу ли я построить окружность с центром в точке пересечения биссектрис и касающаяся сторон треугольника?

d)       Как бы вы могли эту окружность назвать? (Определение 2)

Группа А

Постройте треугольник со сторонами 7 см и 5 см и с углом между ними в 70 ̊ и проведите серединные перпендикуляры с каждой стороны. Ответьте на вопросы:

e)      Пересекаются ли все серединные перпендикуляры в одной точке?

f)       Могу ли я построить окружность с центром в точке пересечения серединных перпендикуляров и проходящая через вершины треугольника?

g)       Как бы вы могли эту окружность назвать?  (Определение 1)

Группа В

Постройте треугольник со сторонами 7 см и 5 см и с углом между ними в 70 ̊ и проведите биссектрису с каждого угла треугольника. Ответьте на вопросы:

c)      Пересекаются ли все биссектрисы в одной точке?

d)      Могу ли я построить окружность с центром в точке пересечения биссектрис и касающаяся сторон треугольника?

h)       Как бы вы могли эту окружность назвать? (Определение 2)

Приложение 3

Теорема 1: Серединные перпендикуляры треугольника пересекаются в одной точке и является центром описанной около треугольника окружности.

        I.            Постройте произвольный треугольник АВС.

     II.            Проведите серединные перпендикуляры к сторонам АВ и АС пересекающиеся в точке D.

  III.            Докажите, что DA = DB.  

  IV.            Аналогично, DA = DС.

    V.            Делаем вывод, что DС= DB, значит точка D _____________ от вершин С и B. То есть лежит на серединном перпендикуляре стороны СB.

  VI.            Значит точка D равно__________ от всех  вершин треугольника. Соответственно является центром ________________ около треугольника окружности.

Теорема 2: Биссектрисы треугольника пересекаются в одной точке и является центром вписанного в треугольник окружности.

        I.            Постройте произвольный треугольник АВС.

     II.            Проведите биссектрисы с вершин А и В пересекающиеся в точке L.

  III.            Докажите, что точка L равноудалена от сторон АС и АВ. Аналогично, и от сторон BC и ВА.

  IV.            Делаем вывод, что точка L ______________ от сторон СА и СВ, значит точка L лежит на биссектрисе угла ___.

    V.            Значит точка D равно__________ от всех  сторон треугольника. Соответственно является центром ________________ в треугольник окружности.

Теорема 1: Серединные перпендикуляры треугольника пересекаются в одной точке и является центром описанной около треугольника окружности.

VII.            Постройте произвольный треугольник АВС.

VIII.            Проведите серединные перпендикуляры к сторонам АВ и АС пересекающиеся в точке D.

  IX.            Докажите, что DA = DB.  

    X.            Аналогично, DA = DС.

  XI.            Делаем вывод, что DС= DB, значит точка D _____________ от вершин С и B. То есть лежит на серединном перпендикуляре стороны СB.

XII.            Значит точка D равно__________ от всех  вершин треугольника. Соответственно является центром ________________ около треугольника окружности.

Теорема 2: Биссектрисы треугольника пересекаются в одной точке и является центром вписанного в треугольник окружности.

  VI.            Постройте произвольный треугольник АВС.

VII.            Проведите биссектрисы с вершин А и В пересекающиеся в точке L.

VIII.            Докажите, что точка L равноудалена от сторон АС и АВ. Аналогично, и от сторон BC и ВА.

  IX.            Делаем вывод, что точка L ______________ от сторон СА и СВ, значит точка L лежит на биссектрисе угла ___.

    X.            Значит точка D равно__________ от всех  сторон треугольника. Соответственно является центром ________________ в треугольник окружности.

Приложение 4

Тест 1

1.      Центр окружности, вписанной в треугольник, совпадает с точкой …

2.      Если точка А равноудалена от сторон данного угла, то она лежит на …

3.      Если точка В лежит на серединном перпендикуляре, проведенному к данному отрезку, то она …

4.      Около любого … можно описать окружность

5.      Центр вписанной в равнобедренный треугольник лежит на …

Тест 2

1.      Центр окружности, описанной около треугольника, совпадает с точкой …

2.      Если точка Д лежит на биссектрисе данного угла, то она ….

3.      Если точка С равноудалена от концов данного отрезка, то она лежит на…

4.      В любой … можно вписать окружность

5.      Центр описанной окружности около прямоугольного треугольника лежит…

Тест 1

1.      Центр окружности, вписанной в треугольник, совпадает с точкой …

2.      Если точка А равноудалена от сторон данного угла, то она лежит на …

3.      Если точка В лежит на серединном перпендикуляре, проведенному к данному отрезку, то она …

4.      Около любого … можно описать окружность

5.      Центр вписанной в равнобедренный треугольник лежит на …

Тест 2

1.      Центр окружности, описанной около треугольника, совпадает с точкой …

2.      Если точка Д лежит на биссектрисе данного угла, то она ….

3.      Если точка С равноудалена от концов данного отрезка, то она лежит на…

4.      В любой … можно вписать окружность

5.      Центр описанной окружности около прямоугольного треугольника лежит…