Тема урока

«Вписанные и описанные четырехугольники»

Вписанные многоугольники

Многоугольник называется вписанным в окружность, если все его вершины принадлежат окружности. Окружность при этом называется описанной около многоугольника.

Теорема 1. Около всякого треугольника можно описать окружность. Ее центр является точкой пересечения серединных перпендикуляров к сторонам треугольника.

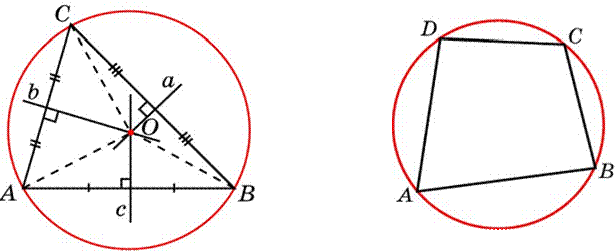
Теорема 2. Суммы противоположных углов четырехугольника, вписанного в окружность, равны 180^о.

Описанные многоугольники

Многоугольник называется описанным около окружности, если все его стороны   касаются этой    окружности.  Сама окружность при этом называется вписанной в многоугольник

Теорема   3.   В   любой треугольник  можно вписать окружность. Ее центром будет точка пересечения биссектрис этого треугольника.

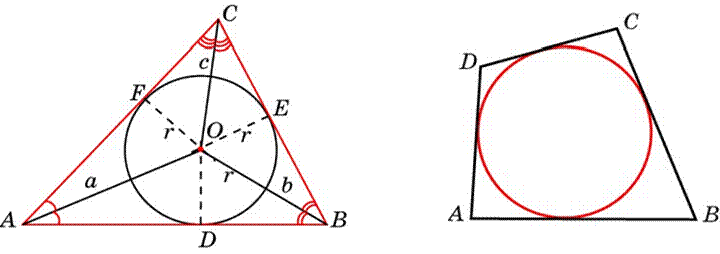
Теорема 4. Суммы противоположных сторон четырехугольника, описанного около окружности, равны.

Вписанные и описанные треугольники

Теорема 5. Отношение стороны треугольника к синусу противолежащего угла равно диаметру описанной окружности.

Теорема   6.   Радиус R окружности, описанной      около правильного треугольника, выражается формулой R  ^2S    , где a, b, c – стороны треугольника S – его площадь.   a b c   

Теорема 7. Радиус r окружности, вписанной в треугольник, выражается формулой r _ ^{a b c } , где a, b, c – стороны треугольника

S – его площадь.                  ^4S

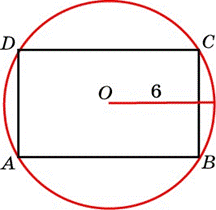
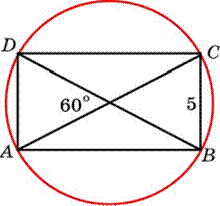
Найдите диагональ прямоугольника, вписанного в окружность радиуса 6.