
Задача 1. Кто в теремочке живет – 10 баллов
Тип задачи: Задача на логическое рассуждение
На одной улице стоят в ряд 4 дома, в каждом из них живет по одному человеку. Их зовут Василий, Семен, Геннадий и Иван. Известно, что все они имеют разные профессии: скрипач, столяр, охотник и врач. Известно, что
· Столяр живет правее охотника.
· Врач живет левее охотника.
· Скрипач живет с краю.
· Скрипач живет рядом с врачом.
· Семен не скрипач и не живет рядом со скрипачом.
· Иван живет рядом с охотником.
· Василий живет правее врача.
· Василий живет через дом от Ивана.
Определите, кто где живет, и запишите начальные буквы имен жильцов всех домов слева направо. Например, если бы в домах жили (слева направо) Кирилл, Олег, Мефодий и Пафнутий, ответ был бы КОМП.
Задача 2. “ Зри в корень ” – 10 баллов
Тип задачи: Задача на системы счисления
Запись числа 6710 в системе счисления с основанием N оканчивается на 1 и содержит 4 цифры. Укажите основание этой системы счисления N.
Задача 3. “ Алгоритм ” – 10 баллов
Тип задачи: Задача на построение алгоритма управления формальным исполнителем
У исполнителя Квадратор две команды, которым присвоены номера:
1. возведи в квадрат
2. вычти 3
Первая из них возводит число на экране во вторую степень, вторая вычитает из числа 3. Составьте алгоритм получения из числа 2 числа 46, содержащий не более 5 команд. В ответе запишите только номера команд. (Например, 2221 – это алгоритм
вычти 3
вычти 3
вычти 3
возведи в квадрат,
который преобразует число 4 в 25.)
Если таких алгоритмов более одного, то запишите любой из них.
Задача 4. “Раз - цепочка, два - цепочка” – 15 баллов
Тип задачи: Задача по кодированию информации
Некоторый алгоритм из одной цепочки символов получает новую цепочку следующим образом. Сначала вычисляется длина исходной цепочки символов; если она нечётна, то дублируется средний символ цепочки символов, а если чётна, то в начало цепочки добавляется буква Г. В полученной цепочке символов каждая буква заменяется буквой, следующей за ней в русском алфавите (А – на Б, Б – на В и т. д., а Я – на А).
Получившаяся таким образом цепочка является результатом работы описанного алгоритма.
Например, если исходной была цепочка УРА, то результатом работы алгоритма будет цепочка ФССБ, а если исходной была цепочка ПУСК, то результатом работы алгоритма будет цепочка ДРФТЛ.
Дана цепочка символов РЕКА.
Какая цепочка символов получится, если к данной цепочке применить описанный алгоритм дважды (т. е. Применить алгоритм к данной цепочке, а затем к результату вновь применить алгоритм)?
Русский алфавит: АБВГДЕЁЖЗИЙКЛМНОПРСТУФХЦЧШЩЪЫЬЭЮЯ
Задача 5. “Фишки” – 30 баллов
Тип задачи: Задача по теории графов
Два игрока играют в следующую игру. На координатной плоскости стоит фишка. Игроки ходят по очереди. В начале игры фишка находится в точке с координатами (-1, -2). Ход состоит в том, что игрок перемещает фишку из точки с координатами (А, В) в одну из трёх точек: или в точку с координатами (А-2, В-3), или в точку с координатами (А+2, В+2), или в точку с координатами (А+1, В+4). Игра заканчивается, как только расстояние от фишки до начала координат превысит число 6. Выигрывает игрок, который сделал последний ход. Кто выигрывает при безошибочной игре обоих игроков – игрок, делающий первый ход, или игрок, делающий второй ход? Каким должен быть первый ход выигрывающего игрока? Ответ обоснуйте, построив таблицу или дерево игры.
Ответы
Задача 1. Кто в теремочке живет
Тип задачи: Задача на логическое рассуждение
|
скрипач |
врач |
охотник |
столяр |
|
Геннадий |
Иван |
Семён |
Василий |
Ответ: ГИСВ
Мах-10 баллов
Задача 2. “ Зри в корень ”
Тип задачи: Задача на системы счисления
Начнем с двоичной системы. Для хранения числа 67 необходимо 7 цифр, т.к. 64<67<128. 128=27.
Троичная система.
Для хранения числа 67 нужно 4 цифры, т.к. 27<67<81. 81=34. Следовательно,троичная система удовлетворяет условию:"число содержит 4 цифры". Теперь необходимо проверить,удовлетворяет данная система условию:"число оканчивается на 1". Для этого нужно перевести 6710 в троичную систему. Но полный певевод делать не надо,т.к. нас интересует только первый остаток, на него и будет оканчиваться 67 в троичной системе.
67 | 3 _
6 22
7
6
1
Остаток равен 1. Следовательно, и второе условие выполнено, поэтому троичная система подходит.
Ответ:_ Основание троичной системы равно 3
Мах-10 баллов
Задача 3. “ Алгоритм ”
Тип задачи: Задача на построение алгоритма управления формальным исполнителем
Ответ: 22212
Мах-10 баллов
Задача 4. “Раз - цепочка, два - цепочка” – 15 баллов
Тип задачи: Задача по кодированию информации
Ответ: ЕТЖЖМВ
Мах-15 баллов
Задача 5. “Фишки” Мах-30 баллов
Тип задачи: Задача по теории графов
Ответ: Выигрывает игрок, делающий первый ход; его ход - (А+2, В+2) дает возможность ему выиграть на втором ходу с любой позиции фишки после хода второго игрока. Хотя у него есть возможность выиграть и если его ход будет (А+1,В+4), что видно из таблицы ниже.
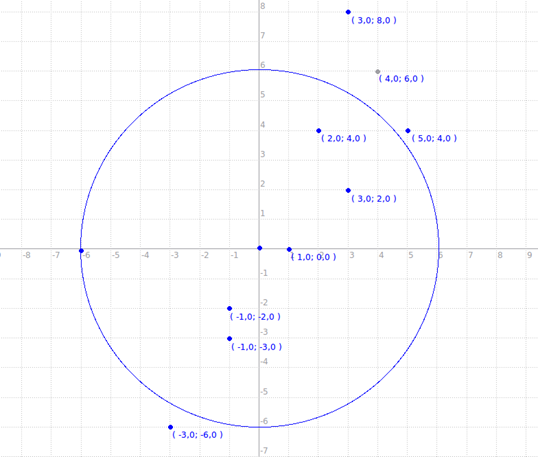
|
Стартовая позиция |
1 ход |
2 ход |
|
|
1 игрок |
2 игрок |
1 игрок |
|
|
(-1.-2) |
(-3,-5) |
(-5,-8) |
- |
|
- |
|||
|
- |
|||
|
(-1,-3) |
- |
||
|
- |
|||
|
- |
|||
|
(-2,-1) |
- |
||
|
- |
|||
|
- |
|||
|
(1,0) |
(-1,-3) |
(-3,-6) |
|
|
(1,-1) |
|||
|
(0,1) |
|||
|
(3,2) |
(1,-1) |
||
|
(5,4) |
|||
|
(4,6) |
|||
|
(2,4) |
(1,1) |
||
|
(4,6) |
|||
|
(3,8) |
|||
|
(0,2) |
(-2,-1) |
(-4,-4) |
|
|
(0,1) |
|||
|
(-1,3) |
|||
|
(2,4) |
(0,1) |
||
|
(4,6) |
|||
|
(3,8) |
|||
|
(1,6) |
(-1,3) |
||
|
(3,8) |
|||
|
(2,10) |
|||
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.