Поделиться
Выч. первообраз.с решен..по граф.и С.Р. .docx
Первообразная.
1.
На рисунке изображён график функции y = F(x) — одной из первообразных функции f(x), определённой на интервале (−3; 5). Найдите количество решений уравнения f(x) = 0 на отрезке [−2; 4].
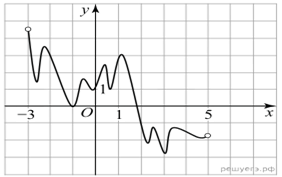
Решение.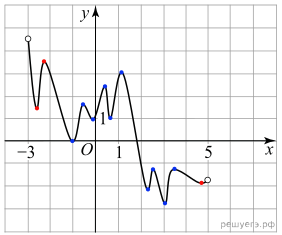 
По определению
первообразной на интервале (−3; 5) справедливо равенство
Следовательно, решениями уравнения f(x)=0 являются
точки экстремумов изображенной на рисунке функции F(x) На рисунке
точки, в которых 
выделены красным и
синим цветом. Из них на отрезке [−2;4] лежат 10 точек (синие точки).
Таким образом, на отрезке [−2;4] уравнение 
имеет 10 решений.
Ответ: 10.
,
2.
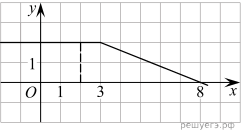
На рисунке изображён график некоторой функции 
(два луча с общей
начальной точкой). Пользуясь рисунком, вычислите F(8) − F(2),
где F(x) — одна из первообразных
функции f(x).
Решение.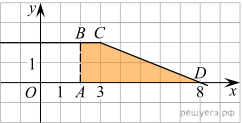 
Разность значений
первообразной в точках 8 и 2 равна площади выделенной на рисунке трапеции 
Поэтому
Ответ:7.
,
3.
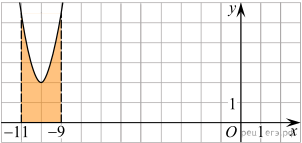
На рисунке изображён график функции y = f(x).
Функция 
—
одна из первообразных функции y = f(x). Найдите
площадь закрашенной фигуры.
Решение. Площадь выделенной
фигуры равна разности значений первообразных, вычисленных в точках 
и 
Имеем:
Приведем другое решение.
Вычисления можно было бы упростить, выделив полный куб:
что позволяет сразу же найти
Приведем ещё одно решение.
Можно было бы найти разность первообразных, используя формулы сокращенного умножения:
Ответ:6.
,
4.
На рисунке изображён график некоторой функции y = f(x).
Функция 
—
одна из первообразных функции f(x). Найдите площадь закрашенной
фигуры.
Решение. Найдем формулу,
задающую функцию 
график которой изображён
на рисунке.
Следовательно, график функции 
получен сдвигом графика
функции 
на 
единиц влево вдоль оси абсцисс. Поэтому искомая площадь фигуры равна
площади фигуры, ограниченной графиком функции 
и отрезком 
оси абсцисс.
Имеем:
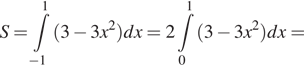
Ответ: 4.
,
5.
На рисунке изображен график некоторой функции 
Пользуясь рисунком,
вычислите определенный интеграл 
Решение. 
Определенный интеграл
от функции 
по отрезку 
дает значение
площади подграфика функции 
на отрезке. Область под
графиком разбивается на прямоугольный треугольник, площадь которого 
и
прямоугольник, площадь которого 
Сумма этих площадей дает искомый интеграл
Ответ:12.
Решить самостоятельно.
1. На рисунке изображён график некоторой функции 𝑦=𝑓(𝑥).
Функция 𝐹(𝑥)=−12𝑥3−3𝑥2−92𝑥+3− одна из первообразных функции 𝑓(𝑥). Найдите площадь закрашенной фигуры
Ответ: 2.
2. На рисунке изображён график функции 𝑦=𝑓(𝑥). Прямая, проходящая через точку (−6;−1), касается этого графика в точке с абсциссой 6. Найдите 𝑓′(6).
Ответ; 0,25
3. На рисунке изображён график некоторой функции 𝑦=𝑓(𝑥) (два луча с общей начальной точкой). Пользуясь рисунком, вычислите 𝐹(−1)−𝐹(−8), где 𝐹(𝑥)− одна из первообразных функции 𝑓(𝑥).
Ответ: 20.
4. Функция 𝐹(𝑥)=−49𝑥3−343𝑥2−2803𝑥−185 — одна из первообразных функции 𝑓(𝑥). Найдите площадь закрашенной фигуры.
Ответ: 6
5. На рисунке изображён график 𝑦=𝐹(𝑥) одной из первообразных некоторой функции 𝑓(𝑥), определённой на интервале (−7;5). Пользуясь рисунком, определите количество решений уравнения 𝑓(𝑥)=0 на отрезке [−5;2].
Ответ: 3
6. На рисунке изображён график 𝑦=𝐹(𝑥) одной из первообразных некоторой функции 𝑓(𝑥) и отмечены десять точек на оси абсцисс: 𝑥1, 𝑥2, 𝑥3, 𝑥4, 𝑥5, 𝑥6, 𝑥7, 𝑥8, 𝑥9, 𝑥10. В скольких из этих точек функция 𝑓(𝑥) положительна?
( На участках возрастания графика первообразной) .
Ответ: 7
7. На рисунке изображены график функции 𝑦=𝑓(𝑥) и касательная к этому графику, проведённая в точке 𝑥0. Уравнение касательной показано на рисунке. Найдите значение производной функции в точке 𝑥0.
Ответ; - 3
(Пояснение: Взять производную от
функции 𝑔(𝑥)=4𝑓(𝑥)−3
и приравнять к угловому коэффициенту к = - 
).
Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.
