
21 ноября
Классная работа
Тема: «Вычисления количества путей в направленном ациклическом графе.
Ход урока
1. Организационный момент (1мин)
листы самооценки раздать учащимся к началу урока
(1 слайд на экране)
Приветствие. Здравствуйте, друзья. Сегодня я хотел бы начать наш урок со слов Шарля де Голля, французского генерала второй мировой войны и выдающегося политика. (2 слайд): "Всегда выбирайте самый трудный путь, на нем вы не встретите конкурентов!".
2. Постановка проблемы. Формулирование условия задачи и предложение решить ее сразу (1 мин)
Говоря о выборе путей, предлагаю вам решить следующую задачу (слайд 3):
|
A |
B |
C |
D |
E |
|
|
A |
2 |
10 |
8 |
16 |
|
|
B |
2 |
9 |
1 |
||
|
C |
10 |
9 |
3 |
4 |
|
|
D |
8 |
1 |
3 |
11 |
|
|
E |
16 |
4 |
11 |
В таблице представлено расстояние между населенными пунктами в километрах. Определить кратчайшее расстояние между пунктами A и E. Какими способами мы можем решить эту задачу.
Предлагайте решения (учащиеся предлагают решения задачи: методом рассуждения).
3. Анализ проблемной ситуации и возможные пути ее решения (2 мин)
Очевидно, что данная форма представления информации в этой задаче (в виде таблицы) не слишком удобна для решения методом рассуждений. Можно предположить что форму представления необходимо изменить.
В геометрии, при решении некоторых задач удобно использовать чертежи (слайд задача показывается в текстовом виде, затем в графическом). А что в информатике позволяет представить условия задачи в графическом виде? (графы). Вспомним, что такое графы. Где в повседневной жизни мы можем столкнуться с графами (навигаторы в машинах, при построении маршрутов на уроках географии, при поездках,
4. Актуализация опорных знаний, умений, навыков, которые потребуются для решения поставленных задач на уроке (5 мин).
(слайд ). Граф - это множество точек или вершин и линий или ребер, соединяющих между собой все или часть этих точек. Граф - это информационная модель объекта или системы объектов.
Какие виды графов вы знаете (слайд 8):
ориентированные (графы, ребрам которых присвоено направление), неориентированные (графы, ребрам которых направление не присвоено). А сейчас давайте с вами определим тему нашего урока, для этого я предлагаю вам следующие высказывания (слайд 9):
Проведем с вами актуализацию знаний, умений, навыков ,которые потребуются нам для решения:
«Когда человек не знает, к какой пристани он держит путь, для него ни один ветер не будет попутным.» Сенека
«От великого до смешного один шаг, но от смешного уже нет пути к великому.»
Лион Фейхтвангер
«Ковыляющий по прямой дороге опередит бегущего, который сбился с пути.» Фрэнсис Бэкон.
«Три пути у человека, чтобы разумно поступать: первый, самый благородный, – размышление; второй, самый легкий, – подражание; третий, самый горький, – опыт.»
5. Формулирование темы урока учащимися самостоятельно (1 мин)
Т.е. тема урока определение путей или если говорить точнее "Пути в графах" (10 слайд).
6. Возврат к проблемной ситуации с задачей и актуализация целей и задач на предстоящем уроке. Учащиеся сами формулируют цели и задачи (1 мин)
(слайд ). А цели и задачи урока следующие (учащиеся предлагают) (13 слайд):
как преобразовать информацию, представленню в табличной форме в граф;
как определить все пути в графе;
как определить кратчайший путь.
7. Разбор задачи с таблицей и преобразование ее в граф. Обход графа и поиск всех возможных путей с вычислением длины пути (15 мин)
 А теперь давайте с вами в
соответствии с целями, которые вы сформулировали вернемся к задче, которую я
предложил в начале урока.
А теперь давайте с вами в
соответствии с целями, которые вы сформулировали вернемся к задче, которую я
предложил в начале урока.
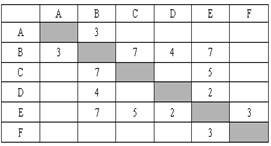
Проанализируем таблицу (14 слайд).
Как мы видим части таблицы, разделенные диагональю симметричны, т.е. содержат одни и те же данные, следовательно можно рассматривать любую данные любой половинки таблицы, разделенной диагональю (15 слайд).
Возьмем верхнюю часть таблицы и приступим к построению графа (16 слайд). Будем действовать в алфавитном порядке и начнем с построения путей из точки А, затем остальные вершины с указанием длины этих линий.
(строим все направления) (17 слайд).
Определим пути в графе и расстояние, пройденное на этом пути (18 слайд). После просмотра всех путей и нахождения их длин, определяем, что кратчайшим путем будет ABDCE (19 слайд).
8. Постановка задачи из демоверсии и ее решение учащимися у доски (5 мин).
Пожалуйста, еще одна подобная задача, желающий выйти и решить ее на доске (выходит учащийся) (20 слайд).
(21 слайд).

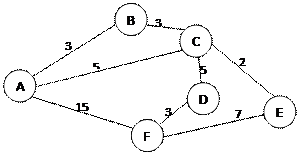 Решение.
В задаче 5 точек, берем верхнюю часть таблицы и строим указанные пути в
алфавитном порядке
Решение.
В задаче 5 точек, берем верхнюю часть таблицы и строим указанные пути в
алфавитном порядке
Указываем все пути в алфавитном порядке:
1. ABCDF - 14 км
2. ABCEF - 15 км
3. ACDF - 13 км
4. ACEF - 14 км
5. AF - 15 км
Физкультминутка (1 мин)
Совершите 15 колебательных движений глазами по горизонтали: справа-налево, затем слева-направо. Совершите 15 колебательных движений глазами по диагонали. Совершите 15 упражнений «Качалочка». То же самое, но вверх. Совершите 15 круговых вращательных движений глазами вначале в правую, а затем в левую сторону.
9. Демонстрация задачи из демоверсии ЕГЭ 2015 года без решения (1 мин)
Теперь хочу показать еще одну задачу данной темы, таблица которой весьма специфична (22 слайд).
Проведем анализ данной таблицы (23 слайд).
Мы видим, что из точки А мы можем попасть только в В и в точку F ведет только один путь из точке Е. Фактические решение задачи сводится к нахождению кратчайшего пути из В в E, что упрощает решение данной задачи.
Подсчет путей в ориентированном графе. ЗАДАЧА № 15.
В этой задаче требуется подсчитать количество путей, ведущих из одной вершины графа в другую. Обычно задачу решают преобразованием графа в дерево. Однако, при сложной структуре графа такое решение становится очень трудоемким. Велика вероятность ошибки. Рассмотрим простой и эффективный способ решения.
В этой задаче мы имеем дело с ориентированным графом (графом, у которого ребра имеют направление). Т.е. ребра имеют вид стрелок. Две вершины, соединенные напрямую стрелкой, называются смежными. Вершина, из которой выходит стрелка, называется предком, а вершина, в которую входит стрелка – потомком.
Несложно понять, что количество путей, которыми можно попасть в некоторую вершину, равно сумме количеств путей предков этой вершины.
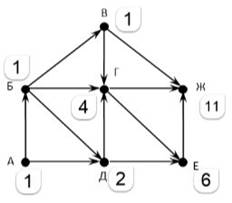
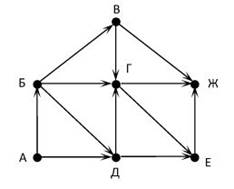 Пример: На рисунке
– схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К. По каждой
дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько
существует различных путей из города А в город Ж?
Пример: На рисунке
– схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К. По каждой
дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько
существует различных путей из города А в город Ж?
Решение:
Каждой вершине, начиная с начальной (A), поставим в соответствие индекс, равный количеству путей, которыми можно попасть в эту вершину. Для вершины A (начало пути) индекс всегда равен 1 (в начало пути можно попасть единственным образом – никуда не двигаясь). Теперь сформулируем правило: индекс вершины равен сумме индексов его предков. Исходя из этого индекс Б равен 1 (предок у Б один – вершина A).
У вершины Д предками являются А и Б, значит индекс вершины Д равен 1+1=2.
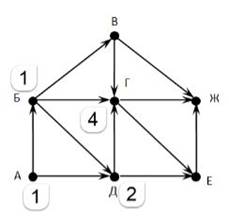
 Очевидно,
что мы можем посчитать индекс только тех вершин, индексы предков которых уже
посчитаны. Например, мы не можем посчитать индекс Г, пока не посчитан индекс В.
Двигаясь последовательно, мы рассчитаем индексы всех вершин.
Очевидно,
что мы можем посчитать индекс только тех вершин, индексы предков которых уже
посчитаны. Например, мы не можем посчитать индекс Г, пока не посчитан индекс В.
Двигаясь последовательно, мы рассчитаем индексы всех вершин.
Индекс вершины Ж и будет ответом задачи.
Ответ: 11
10. Подведение итогов урока (2 мин)
На сегодняшнем уроке мы с вами вспомнили, что такое граф и типы графов
научились строить графы и определять пути в нем на основе табличной модели;
на основе анализа всех путей в графе научились делать заключение о том какой путь самый короткий.
13. Домашнее задание (1 мин)
Выполнение практической работы на компьютере для закрепления навыков преобразования таблицы в граф и поиска путей в нем с использованием текстового редактора Word (10 мин)
Вы получили задание по карточке. Вам нужно преобразовать таблицу в граф и кратчайший путь. Выполнять данную задачу вы будете с использованием текстового редактора Word. Обращаю ваше внимание на аккуратность и правильность построения графа с использованием "Фигур", вершины графа обозначать окружностями с вписанными значениями, ребра графа - линии с подписанными длинами путей. Каждый путь вместе с суммарным расстоянием выписываете отдельно.
После завершения работы, сохраните свой файл. В имени файла укажите тему сегодняшнего урока (Пути в графах), фамилию и класс. Данный файл нужно скинуть в вк своему учителю по информатике.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.