Выпускная квалификационная работа Комплекс заданий исследовательского характера как средство развития математической г

Министерство общего и профессионального образования

Государственное бюджетное профессиональное образовательное учреждение

Свердловской области

«Камышловский педагогический колледж»

Выпускная квалификационная работа

Комплекс заданий исследовательского характера как средство развития математической грамотности младших школьников

44.02.02 Преподавание в начальных классах

Исполнитель:

Койнова Т.Ю.,

студентка 4^А группы

Руководитель:

Мадыгина Т.А.,

преподаватель

Камышлов, 2017
ОГЛАВЛЕНИЕ

Пояснительная записка3

Теоретико-методологическое обоснование комплекса заданий исследовательского характера как средство развития математической грамотности младших школьников 3

Обоснование структуры и содержания комплекса заданий исследовательского характера как средство развития математической грамотности младших школьников 26

Анализ ресурсов и условий реализации комплекса заданий исследовательского характера как средство развития математической грамотности младших школьников 32

Педагогические условия реализации комплекса заданий исследовательского характера как средство развития математической грамотности младших школьников 42

Оценка результативности комплекса заданий исследовательского характера как средство развития математической грамотности младших школьников. .49

Комплекс заданий исследовательского характера как средство развития математической грамотности младших школьников……………… ……………………………………………….…59

Список литературы……………………………………………………61

Приложения
Пояснительная записка

Теоретико-методологическое обоснование комплекса заданий исследовательского характера как средство развития математической грамотности младшего школьника

В современном обществе существенно возрастает значимость качества математического образования. Без преувеличения можно утверждать, что высокое качество математического образования в стране является основой её национальной безопасности и экономического могущества. Этот тезис подтверждает и многолетний отечественный опыт. Именно он стимулировал инициативу правительства России, объявленного Председателем Правительства Медведевым Д. А., о радикальном улучшении качества математического образования в России в ближайшем будущем.[3]

«Особый акцент будет сделан на развитие математического образования как основы для создания высокотехнологичной экономики.

Основой высокого уровня математического образования на разных ступенях обучения является математическая грамотность подрастающего поколения. Поэтому обеспечение математической грамотности школьников является первоочередной задачей в деле обеспечения добротности школьного математического образования. А это является основой добротности математического образования в профессиональной школе.

Задания исследовательского характера носят такой характер, когда в процессе решения у младших школьников возникает необходимость сосредоточиться на сути выполняемых вычислительных действий, исследовать их механизм. Задания исследовательского характера способствуют развитию таких качеств вычислительных умений, как осознанность, рациональность, действенность, правильность.

Именно поэтому закладка основных содержательных линий математического образования, включающего в себя, в том числе и общие исследовательские умения, через математическую грамотность происходит на начальной стадии обучения. Таким образом, развитие математической грамотности обучающихся, через решение заданий исследовательского характера — одна из актуальных задач современного образования.

В ходе работы были выявлены противоречия:

- между требованиями ФГОС НОО к результату образования, в том числе и к математической компетентности выпускников начальной школы и реальными недостаточно высокими результатами математической грамотности обучающихся;

- между достаточной теоретической изученностью проблемы формирования математической грамотности младших школьников и трудностями в отборе действенных педагогических средств по формированию математической грамотности обучающихся в том числе и средствами заданий исследовательского характера;

-между необходимостью развития математической грамотности у младших школьников и недостаточным количеством методических пособий, позволяющих целенаправленно и планомерно развивать математическую грамотность младших школьников.

Из данных противоречий нами была выделена следующая проблема дипломного проекта: недостаточность методической продукции, которая позволит развивать математическую грамотность.

В соответствии с темой были определены цель, задачи, исследования.

Цель дипломного проекта: разработать, обосновать и на основе пробации дать оценку результативности комплекса заданий исследовательского характера, направленного на развитие математической грамотности младшего школьника.

Задачи:

1) осуществить теоретико-методологическое обоснование комплекса заданий исследовательского характера как средства развития математической грамотности младших школьников;

2) разработать, обосновать структуру и содержание комплекса заданий исследовательского характера как средства развития математической грамотности младших школьников;

3) проанализировать ресурсы и условия реализации комплекса заданий исследовательского характера, направленные на развитие математической грамотности младших школьников и дать оценку его результативности;

4) оценить результативности применения комплекса заданий исследовательского характера, направленного на развитие математической грамотности младших школьников.

Объект проектирования: процесс развития математической грамотности у младших школьников.

Форма проектирования: комплекс заданий исследовательского характера направленные на развитие математической грамотности младшего школьника.

Обоснование выбора формы: нами была выбрана такая форма как комплекс - это издание, содержащие ряд разноуровневых заданий, а также различных официальных, научных и информационных материалов на определенную тему. В нашем случае в комплекс включены задания исследовательского характера, направленные на развитие математической грамотности.

Новизна продукта заключается в том, что созданная методическая разработка представляет собой комплекс заданий исследовательского характера, последовательная реализация которого способствует успешному развитию математической грамотности у обучающихся 3 класса.

Понятие математической грамотности начало формироваться в конце ХХ столетия в исследованиях Международной ассоциации по оценке учебных достижений учащихся ІЕА. В этих исследованиях под математической грамотностью понимали «готовность выпускников средней школы справляться с жизненными проблемами, для решения которых нужно использовать некоторые математические знания». Здесь под математической грамотностью понимается «способность человека определять и понимать роль математики в мире, в котором он живет, высказывать хорошо обоснованные математические суждения и использовать математику так, чтобы удовлетворять в настоящем и будущем потребности, присущие созидательному, заинтересованному и мыслящему гражданину» [10] Позднее содержание этого понятия уточнялось и видоизменялось. И под математической грамотностью современные исследователи понимают способность учащихся:

1) распознавать проблемы, которые возникают в окружающей действительности и могут быть решены средствами математики;

2) формулировать эти проблемы на языке математики;

3) решать эти проблемы, используя математические факты и методы;

4) анализировать и использовать математические методы решения;

5) интерпретировать полученные результаты с учетом поставленной проблемы;

6) формулировать и записывать результаты решения.

Математическая грамотность, по словам А.А. Леонтьева, предусматривает способность человека использовать приобретенные в течение жизни знания для решения широкого диапазона жизненных задач в различных сферах человеческой деятельности, общения и социальных отношений.

С. Березин дает такое понимание математической грамотности: «Математическая грамотность - умение правильно применять математические термины, наличие необходимых математических знаний и сведений для выполнения работы (решение проблемы) в конкретной предметной области».

Из вышесказанного рождается термин функциональная математическая грамотность, которая предполагает способность учащегося использовать математические знания, приобретенные им за время обучения в школе, для решения разнообразных задач межпредметного и практико-ориентированного содержания, для дальнейшего обучения и успешной социализации в обществе.

А. И. Савенков отмечает, что в школе уже много лет продолжается противодействие традиционного и исследовательского обучения. По-прежнему традиционное обучение, строится не на методах самостоятельного, творческого исследовательского поиска, а на репродуктивной деятельности, направленной на усвоение уже готовых, кем-то добытых истин. Благодаря этому обучению у ребенка в значительной мере утрачивается главная черта исследовательского поведения - поисковая активность. Итогом становится потеря любознательности, способности самостоятельно мыслить, делая в итоге практически невозможными процессы самообучения, самовоспитания, а, следовательно, и саморазвития.

Именно поэтому подготовка ребенка к исследовательской деятельности, обучение его умениям и навыкам исследовательского поиска становится важнейшей задачей образования и современного учителя. Закладка основных содержательных линий математического образования, включающего в себя, в том числе и общие исследовательские умения, происходит также на начальном этапе обучения. Уже на начальном этапе изучения математики возможно использование элементов учебных математических исследований, организованных как задания исследовательского характера. Таким образом, формирование навыков исследовательской деятельности, учащихся посредством развития математической грамотности — одна из актуальных задач современного образования.

По словам Ковалевской О.Н., Васильевой И.П., Мудровой О.И. математическая грамотность это - способность человека определять и понимать роль математики в мире, в котором он живет, высказывать хорошо обоснованные математические суждения и использовать математику так, чтобы удовлетворять в настоящем и будущем потребности, присущие созидательному, заинтересованному и мыслящему гражданину.

Компоненты математической грамотности:

1) воспроизведение математических фактов, методов и выполнение вычислений;

2) установление связей и интеграции материала из разных математических тем, необходимых для решения поставленной задачи;

3) математические размышления, требующие обобщения и интуиции.

Средства развития математической грамотности, применимы через:

1) практико-ориентированный подход;

2) дифференцированный подход;

3) развивающий и системно-деятельностный подходы.

Умения, применительно к математическому содержанию:

1) умение анализировать текст, использовать информацию, представленную в различных формах;(переход от одной ситуации к другой, придерживаться инструкции, видеть проблему, обосновать действия, оформление в виде таблицы , диаграммы и прочее);

2) умение одновременно удерживать несколько условий, в том числе, конфликтующих друг с другом;(3 уровня: 1- репродуктивный, 2-рефлексивный, 3-функциональный);

3) умение использовать моделирование с целью выделения существенных отношений к задаче; (графики, знаки, формулы);

4) умение выявлять закономерности в структурированных объектах; (делать выводы);

5) умение осуществлять пробные действия при поиске решения; (проблемные ситуации на уроке);

6) умение контролировать ход и результат решения задачи (карта достижений - выбирать материал, который необходим для решения задачи; осознать и обозначить свой путь движения в предмете и делать предположения о дальнейших продвижениях).

Эти умения являются индикаторами математической грамотности и формируются за счет включения в урок заданий, направленных на формирование данных умений.

Однако, существуют проблемы, которые мешают развитию математической грамотности:

1) низкий уровень вычислительных навыков;

2) отсутствие практической направленности в математике (дефицит практико-ориентированного подхода в обучении);

3) репродуктивный метод в преподавании (натаскивание на решение по аналогии);

4) неумение организовать свой домашний учебный труд, ответственность за выполнение домашнего задания;

5) формальное изучение геометрии, как предмета формирующего пространственное мышление;

6) не восприятие учащимися необходимости заучивания основ теоретических понятий (формул, правил, теорем и т.д.).

Математическая грамотность учащихся может формироваться с помощью компетентностно-ориентированных заданий, интегрированных заданий и информационных технологий.

Интегрированные задания (математика-информатика, физика-математика, экономика-математика, астрономия-математика, география-математика).

Кроме того, одним из главных средств развития математической грамотности являются информационные технологии (персональный сайт учителя, дистанционные конкурсы, олимпиады, веб-квесты).

Персональный сайт «Математика на 5+»:

1) создаёт условия для максимального учета индивидуальных образовательных возможностей и потребностей учащихся, раскрытия творческого потенциала учащихся;

2) дополняет учебник теми элементами, которые он реализовать не может;(интерактивные упражнения, онлайн тестирование, видеоуроки, сборники тестов для самоподготовки);

3) обеспечивает учебно-методическое сопровождение учебного предмета;(презентации к урокам, лекции и т.д., раздаточный материал);

4) позволяет осуществлять различные виды контроля и подготовку к нему (к ЕНТ, ВОУД, текущий и промежуточный контроль, тренажеры);

5) самостоятельная работа с тестовыми заданиями по теме, в том числе в формате онлайн-тестирования, позволяет учащемуся оценивать степень разрешенности проблемы и характер достигнутого продвижения;

6) использование интерактивных упражнений, созданных с помощью веб-сервиса http://learningapps.org/;

7) онлайн-тестирование с помощью сервиса http://onlinetestpad.com/ru-ru/Main/TestMaker.aspx и видеоуроки.

Данные формы работы способствуют развитию информационно-образовательной среды, направленной на повышение математической грамотности учащихся, обеспечивающей личное саморазвитие, самостоятельность в приобретении знаний, формирующей коммуникативные навыки, умения использовать информацию и технологии, решать проблемы, предприимчивость и креативность. Данные диагностики уровня информационной и технологической культуры, познавательной активности, результаты внешней и внутренней оценки качества обучения, анализ личных достижений обучающихся подтверждают эффективность созданных педагогических условий. На уроках математики, одним из актуальных методов является метод исследования, именно поэтому для нашего комплекса мы выбрали именно его, так как он содержит следующие учебные элементы:

1) ситуация успеха. Ученикам предлагается задачи, которые каждый ученик решает без особых затруднений;

2) ситуация затруднения (ощущения проблемы). Ученикам предлагается задача, похожая на предыдущие, но решить до конца они ее не могут, так как они не имеют еще необходимых знаний;

3) постановка учебной проблемы. Учащиеся, осознав проблему, проговаривают ее, говорят, каких знаний им не хватает, для того чтобы решить задачу, выдвигают гипотезы о возможных путях решения задачи;

4) решение учебной проблемы. Если предложено несколько путей решения проблемы, то возможно деление на группы. Организует деятельность групп лидер, тот ученик, который предложил путь решения незнакомой задачи.

В ‏ㅤ3 ‏ㅤклассе:

Учащиеся ‏ㅤпродолжают ‏ㅤзнакомиться ‏ㅤс ‏ㅤтеорией ‏ㅤисследования, ‏ㅤметодами ‏ㅤисследований. ‏ㅤНа ‏ㅤуроках ‏ㅤиспользуются ‏ㅤигровые ‏ㅤметоды, ‏ㅤпутешествия, ‏ㅤсказочный ‏ㅤматериал, а так же:

1) проводятся ‏ㅤколлективные ‏ㅤисследования ‏ㅤна ‏ㅤзаданную ‏ㅤтему. ‏ㅤУ ‏ㅤтретьеклассников ‏ㅤактивность ‏ㅤвыше, ‏ㅤнеординарных ‏ㅤподходов ‏ㅤи ‏ㅤпредложений ‏ㅤв ‏ㅤосуществлении ‏ㅤисследовательской ‏ㅤдеятельности.

2) осуществляется ‏ㅤучащимися ‏ㅤсамостоятельное ‏ㅤдолговременное ‏ㅤисследование ‏ㅤс ‏ㅤприменением ‏ㅤимеющихся ‏ㅤзнаний ‏ㅤи ‏ㅤумений ‏ㅤ(осуществляется ‏ㅤпоиск ‏ㅤинформации, ‏ㅤучатся ‏ㅤвыделять ‏ㅤглавное, ‏ㅤформулировать ‏ㅤопределения, ‏ㅤставить ‏ㅤпростейшие ‏ㅤопыты, ‏ㅤнаблюдать, ‏ㅤсоставлять ‏ㅤдоклады). ‏ㅤУчащиеся ‏ㅤпроводят ‏ㅤопросы, ‏ㅤанкетирования.

3) ход ‏ㅤисследований ‏ㅤобсуждается, ‏ㅤучителем ‏ㅤоказывается ‏ㅤконсультативная ‏ㅤпомощь. ‏ㅤК ‏ㅤконцу ‏ㅤгода ‏ㅤбольшая ‏ㅤчасть ‏ㅤучащихся ‏ㅤдолжна ‏ㅤс ‏ㅤдостаточной ‏ㅤстепенью ‏ㅤсамостоятельности ‏ㅤвыбирать ‏ㅤтему ‏ㅤисследования, ‏ㅤсоставлять ‏ㅤплан ‏ㅤисследования, ‏ㅤопределять ‏ㅤодну-две ‏ㅤзадачи, ‏ㅤнаходить ‏ㅤматериал, ‏ㅤпредставлять ‏ㅤдоклад ‏ㅤс ‏ㅤпоказом.

Задания ‏ㅤисследовательского ‏ㅤхарактера, ‏ㅤбудут ‏использованы ‏ㅤво ‏ㅤвремя ‏ㅤпреддипломной ‏ㅤпрактики ‏ㅤна ‏ㅤуроках ‏ㅤматематики. ‏ㅤДанные ‏ㅤзадания ‏ㅤбудут способствовать ‏ㅤактивизации ‏ㅤмыслительной ‏ㅤи ‏ㅤпоисковой ‏ㅤдеятельности ‏ㅤшкольников.

Можно ‏ㅤсделать ‏ㅤвывод: ‏ㅤисследовательская ‏ㅤдеятельность ‏ㅤоткроет ‏ㅤогромные ‏ㅤвозможности ‏ㅤдля ‏ㅤсотрудничества ‏ㅤучеников ‏ㅤи ‏ㅤученика ‏ㅤс ‏ㅤучителем. ‏ㅤОбязанности ‏ㅤучителя ‏ㅤпри ‏ㅤэтом будут‏ㅤне ‏ㅤменее ‏ㅤсложны ‏ㅤи ‏ㅤответственны, ‏ㅤчем ‏ у ученика. ‏ㅤНеобходим ‏ㅤтщательный ‏ㅤподбор ‏ㅤи ‏ㅤанализ ‏ㅤсодержания ‏ㅤучебного ‏ㅤматериала, ‏ㅤна ‏ㅤоснове ‏ㅤкоторого ‏ㅤучитель ‏ㅤумеет ‏ㅤвыделить ‏ㅤте ‏ㅤже ‏ㅤвопросы, ‏ㅤкоторые ‏ㅤдоступны ‏ㅤучащимся ‏ㅤдля ‏ㅤсамостоятельной ‏ㅤпроработки ‏ㅤи ‏ㅤважны ‏ㅤдля ‏ㅤразвития ‏ㅤматематической грамотности.

Учебное ‏ㅤисследование ‏ㅤмладшего ‏ㅤшкольника, ‏ㅤтак ‏ㅤже ‏ㅤкак ‏ㅤи ‏ㅤисследование, ‏ㅤпроводимое ‏ㅤвзрослым ‏ㅤисследователем, ‏ㅤнеизбежно ‏ㅤвключает ‏ㅤосновные ‏ㅤэлементы: ‏ㅤвыделение ‏ㅤи ‏ㅤпостановку ‏ㅤпроблемы ‏ㅤ(выбор ‏ㅤтемы ‏ㅤисследования); ‏ㅤвыработку ‏ㅤгипотез; ‏ㅤпоиск ‏ㅤи ‏ㅤпредложение ‏ㅤвозможных ‏ㅤвариантов ‏ㅤрешения; ‏ㅤсбор ‏ㅤматериала; ‏ㅤанализ ‏ㅤи ‏ㅤобобщение ‏ㅤполученных ‏ㅤданных; ‏ㅤподготовку ‏ㅤи ‏ㅤзащиту ‏ㅤитогового ‏ㅤпродукта.

Понятие математическая грамотность имеет главный признак - готовность человека применять математику в различных ситуациях, связанных с жизнью. Именно поэтому, задания, призванные исследовать состояние математической грамотности учеников, в подавляющем большинстве имели четко выраженную прикладную направленность и их решение предусматривало, прежде всего, владение учащимися приемами деятельности прикладного характера.

Математическая грамотность содержит такие три уровня компетентности:

1) первый уровень включает воспроизведение математических фактов, методов и выполнения вычислений;

2) второй - установление связей и интеграцию материала из разных математических тем, необходимого для решения поставленной проблемы;

3) третий - математические размышления, требующие обобщения и интуиции.

Компетенция - это готовность (способность) ученика использовать усвоенные знания, учебные умения и навыки, а также способы деятельности в жизни для решения практических и теоретических задач.

Исследователи компетентностного подхода к обучению предлагают несколько классификаций ключевых компетенций. По одной из них (автор А.В. Хуторской)[7],ключевыми образовательными компетенциями являются:

1) ценностно-смысловая - готовность видеть и понимать окружающий мир, ориентироваться в нем, осознавать свою роль и предназначение, уметь выбирать целевые и смысловые установки для своих действий и поступков, принимать решения;

2) общекультурная - осведомленность обучающегося в особенностях национальной и общечеловеческой культуры, духовно-нравственных основах жизни человека и человечества, отдельных народов, культурологических основах семейных, социальных, общественных явлениях и традициях, роли науки и религии в жизни человека, их влиянии на мир, эффективных способах организации свободного времени;

3) учебно-познавательная - готовность обучающегося к самостоятельной познавательной деятельности: целеполаганию, планированию, анализу, рефлексии, самооценке учебно-познавательной деятельности, умению отличать факты от домыслов, владению измерительными навыками, использованию вероятностных, статистических и иных методов познания;

4) информационная - готовность обучающегося самостоятельно работать с информацией различных источников, искать, анализировать и отбирать необходимую информацию, организовывать, преобразовывать, сохранять и передавать ее;

5) коммуникативная - включает знание необходимых языков, способов взаимодействия с окружающими и удаленными людьми и событиями, предусматривает навыки работы в группе, владение различными специальными ролями в коллективе. Обучающийся должен уметь представить себя, написать письмо, анкету, заявление, задать вопрос, вести дискуссию и т. д.;

6) социально-трудовая - владение знаниями и опытом в гражданско-общественной деятельности (выполнение роли гражданина, наблюдателя, избирателя, представителя), в социально-трудовой сфере (права потребителя, покупателя, клиента, производителя), в области семейных отношений и обязанностей, в вопросах экономики и права, в профессиональном самоопределении;

7) личностная (самосовершенствование) - готовность осуществлять физическое, духовное и интеллектуальное саморазвитие, эмоциональную саморегуляцию и самоподдержку.

В приведенном перечне нас интересует первая позиция, рассмотрение учебно-познавательной ключевой компетенции на предмет формирования математической компетенции.

Математическая компетенция - это способность структурировать данные (ситуацию), вычленять математические отношения, создавать математическую модель ситуации, анализировать и преобразовывать ее, интерпретировать полученные результаты. Иными словами, математическая компетенция учащегося способствует адекватному применению математики для решения возникающих в повседневной жизни проблем.

Существует несколько определений математической компетентности. Остановлюсь на определении разработчиков международного исследования PISA, которые считают, что: «математическая компетентность» - наиболее общие математические способности и умения, включающие математическое мышление, письменную и устную математическую аргументацию, постановку и решение проблемы, математическое моделирование, использование математического языка, современных технических средств.

Совокупность компетенций, наличие знаний и опыта, необходимых для эффективной деятельности в заданной предметной области, называют компетентностью.

Однако компетентность нельзя трактовать только как сумму предметных знаний, умений и навыков. Это - приобретаемое в результате обучения и жизненного опыта новое качество, увязывающее знания и умения учащегося со спектром интегральных характеристик качества подготовки, в том числе и со способностью применять полученные знания и умения к решению проблем, возникающих в повседневной практике.

Развитие математической компетентности без активизации познавательной деятельности ученика, практически невозможно. Вот почему в процессе обучения необходимо систематически возбуждать, развивать и укреплять познавательную активность учащихся и как важный мотив учения, и как стойкую черту личности, и как мощное средство воспитывающего обучения, повышения его качества.

Математическая грамотность непосредственно связана с математическим моделированием, так как его применение в математике используется для решения жизненных задач состоит в выделении существенных характеристик реальных объектов и отношений между ними, игнорировании несущественных и их замене математическими объектами и связями между ними. Процесс такого замещения называют математическим моделированием.

Математическими моделями называют приближенные описания какого-то класса явлений внешнего мира с помощью математических объектов и отношений между ними и задач, с ними связанных.

Процесс математического моделирования состоит из трех этапов:

1) выбор или построение математической модели, соответствующей данной задаче;

2) исследование построенной модели, то есть решение математической задачи;

3) содержательное толкование результатов исследования, установление соответствия полученного результата целям исследований.

Построение математической модели основывается на абстрагировании от всех свойств объекта познания, кроме количественных и пространственных. При построении математической модели всегда возникает необходимость пренебрегать теми или иными сторонами реальности, делать определённые допущения, упрощающие реальную ситуацию.

Построение математической модели является первым этапом применения метода математического моделирования. Он является одним из наиболее сложных и наиболее ответственных этапов исследования, так как от него зависит успешность исследования в целом. Во многих случаях правильный выбор модели означает решение задачи наполовину.

Сложность построения математической модели связана со многими факторами. Среди них особенно значимыми является:

1) владение знаниями и опытом в той сфере, которая моделируется;

2) владение математическими знаниями и умениями, которые могут быть применены для построения математической модели и ее исследования.

Построение математической модели основывается на пренебрежении всеми свойствами и отношениями объекта познания, кроме тех, которые связаны с количественными отношениями и пространственными формами. Более того, при этом рассматриваются наиболее существенные из них, определяющие сущность объекта или процесса.

Для построения математических моделей используют разнообразные математические объекты и отношения между ними: числа, фигуры, функции, уравнения, неравенства, отношения подобия и т. п.

Результатом первого этапа математического моделирования при решении прикладной задачи является построение математической модели, то есть формирование математической задачи. Ее решение составляет второй этап применения метода математического моделирования.

Решение математических задач в прикладных исследованиях имеет свою специфику. Эта специфика связана с тем, что основной целью такого исследования является получение результата, который можно использовать на практике, причем, желательно с наименьшими расходами и достаточным качеством. Таким образом, решение математической задачи не является самоцелью. Оно является средством и подчинено общим целям прикладного исследования. Поэтому в исследовании математической модели главным является принцип соответствия внешней и внутренней правдоподобности.

Выбор методов исследования математической модели, точность приближений и вычислений в процессе решения математической задачи должны отвечать как сущности математической модели (внутренняя правдоподобность), так и качеству математической модели (внешняя правдоподобность).

Третий этап применения метода математического моделирования является наиболее сложным и ответственным. Именно на этом этапе выявляется эффективность проведенной работы и возможность использования результатов исследования математической модели.

Первый шаг этого этапа заключается в переводе результатов решения математической задачи на язык исходной прикладной задачи. Этот перевод состоит из декодирования знаков, их значений, формул и т. п. В процессе такого перевода выясняется соответствие результатов исследования содержанию исходной прикладной задачи. Результаты, не отвечающие этому требованию, тщательным образом анализируются.

Результаты, которые получены на основе исследования математической модели, всегда имеют приближенный характер. Их точность определяется, в главном, степенью адекватности (соответствия) математической модели сущности исследуемого объекта. И этот вопрос является самым сложным в применении метода математического моделирования.

Исследование адекватности модели объекта состоит из нескольких мероприятий:

1) установление непротиворечивости математической модели;

2) априорной проверки адекватности на основе знаний законов и опыта их применения;

3) экспериментальной проверки адекватности;

4) установление количественной точности результата.

На третьем этапе в построенную модель могут вноситься изменения, делающие ее реальнее, совершенней, хотя, как правило, и более сложной. Необходимость в уточнении математических моделей определяется требованиями практики.

На основе анализа методической и психолого – педагогической литературы можно выделить следующие уровни заданий для проверки математической грамотности.

Принято считать три уровня математической компетентности: уровень воспроизведения, уровень установления связей, уровень рассуждений.

Первый уровень (уровень воспроизведения) - это прямое применение в знакомой ситуации известных фактов, стандартных приемов, распознавание математических объектов и свойств, выполнение стандартных процедур, применение известных алгоритмов и технических навыков, работа со стандартными, знакомыми выражениями и формулами, непосредственное выполнение вычислений.

Второй уровень (уровень установления связей) строится на репродуктивной деятельности по решению задач, которые, хотя и не являются типичными, но все же знакомы учащимся или выходят за рамки известного лишь в очень малой степени. Содержание задачи подсказывает, материал какого раздела математики надо использовать и какие известные методы применить. Обычно в этих задачах присутствует больше требований к интерпретации решения, они предполагают установление связей между разными представлениями ситуации, описанной в задаче, или установление связей между данными в условии задач.

Третий уровень (уровень рассуждений) строится как развитие предыдущего уровня. Для решения задач этого уровня требуются определенная интуиция, размышления и творчество в выборе математического инструментария, интегрирование знаний из разных разделов курса математики, самостоятельная разработка алгоритма действий. Задания, как правило, включают больше данных, от учащихся часто требуется найти закономерность, провести обобщение и объяснить или обосновать полученные результаты.

Характеристика этих уровней дает возможность прийти к таким выводам:

1) компетентность проявляется в решении задач, нуждающихся в применении приобретенных умений в условиях, несколько отличающихся от знакомых учащимся. При этом не предусматривается значительный объем математических умений, нестандартность заданий обеспечивается, прежде всего, их прикладной направленностью;

2) уровни компетентности отличаются составом когнитивных приемов деятельности (распознавание, воспроизведение, установление связей между данными в условии задачи, интерпретация решения, установление закономерностей, проведения обобщения и т. п.).

Как видим, для определения уровня математической компетентности исследовалось владение учащимися определенными приемами деятельности, входящими в состав такого обобщенного приема деятельности как математическое моделирование.

Приведенное выше описание математической грамотности в международных исследованиях и уровней ее овладения (уровней компетентности) дает возможность прийти к главному выводу о том, что приоритетным направлением усовершенствования математического образования является обеспечение математической грамотности высокого уровня компетентности.

Именно обеспечение практической и прикладной направленности математического образования и составляет сущность компетентностного подхода к обучению математике. Имеется в виду направленность на решение жизненных проблем, к действиям в реальных условиях, в различных плоскостях: когнитивной, операциональной, эмоционально-ценностной.

Обеспечение математической грамотности высокого уровня компетентности заключается в гармоничном формировании трех приемов деятельности:

1) моделировать с помощью математики объекты окружающего мира и отношения между ними;

2) оперировать определенным составом математических знаний и умений;

3) создавать стратегии решения задач.

Целенаправленное формирование умений решать задачи вообще, математические в частности, является, безусловно, одним из важнейших путей усовершенствования образования. А это, в свою очередь, связано с формированием навыков анализа условия задачи, поиска путей её решения, осмысления результатов решения.

Формирование определенной системы математических знаний всегда было в центре внимания в математическом образовании. Объем этой системы является слишком большим с общеобразовательных позиций, а качество владения ими – недостаточно высоким. А главное, формирование этой системы знаний и умений не связана органически с формированием умений применять математику и стратегией решения задач.

Практическая значимость:

Материалы исследования будут способствовать расширению области обучения в начальной школе, помогут учителям систематически построить работу учеников 3 класса на занятиях математики при решении заданий исследовательского характера, способствуя развитию математической грамотности у младших школьников. Результаты исследования могут быть использованы учителями начальных классов и студентами в практической деятельности, во время проведения педагогических производственных практик.

Обоснование структуры и содержания комплекса заданий исследовательского характера как средство развития математической грамотности младшего школьника

Проектирование комплекса направлено на подбор и систематизацию заданий исследовательского характера, применение которых при организации учебной деятельности школьников позволит развивать умения, направленные на развитие математической грамотности у обучающихся.

Комплекс позволит детям выбрать задания того уровня, с которым они лучше справятся, и будет возможность попробовать выполнить задание другого уровня.

На этапе анализа объекта проектирования необходимо, прежде всего, определить, что мы будем проектировать: ситуацию, систему или процесс. В качестве объекта проектирования выбран процесс развития математической грамотности у младших школьников. В нашей работе объект проектирования разработан на уровне проектирования (создание проекта), так как модель можно использовать на практике. При проектировании целесообразной является следующая форма проектирования – комплекс заданий исследовательского характера, направленного на развитие математической грамотности у младших школьников.

Задание-вид поручения учителя учащимся, в котором содержатся требования выполнить какие-либо учебные действия. С целью выработки у учащихся умений и навыков им даются задания на выполнение упражнений и на решение задач. Эти задания расположены в такой последовательности, чтобы обеспечить индивидуальную работу в зависимости от уровня подготовленности учащихся.

В процессе работы над проблемой исследования предпочтение отдано такой форме проектирование как комплекс.

Комплекс – это издание, содержащие ряд разноуровневых заданий, а также различных официальных, научных и информационных материалов на определенную тему. В нашем случае в комплекс включены задания исследовательского характера, направленные на развитие математической грамотности у обучающихся 3 класса. Задание–это определённая информация, предусматривающая целенаправленное действие учащихся по известному алгоритму или деятельности по разрешению конкретной проблемной ситуации. Проектирование комплекса предполагало его моделирование, проектирование и конструирование.

Первый этап – педагогическое моделирование-это разработка целей и основной идеи создаваемого комплекса. На этапе проектирования мы определили его составные части и внутреннюю структуру каждой части. В рамках этих этапов осуществлён анализ литературы по проблеме исследования. На этапе конструирования осуществлялся процесс наполнения комплекса конкретными заданиями по определенным уровням.

Просмотрев и проанализировав ряд комплексов, мы увидели следующую структуру, которой придерживались в своем комплексе. Разработанный комплекс имеет следующую структуру: титульный лист, введение (вступительное слово), задания по уровням.

Охарактеризуем данные части:

1) на титульном листе указывается название комплекса, автор, год издания, место издания;

2) аннотация содержит краткое описание назначения комплекса заданий исследовательского характера по математике, его значимость;

3) в пояснительной записке указывается актуальность, основание структурирование системы заданий исследовательского характера, перечень частей, цель, рекомендации по использованию, для кого предназначен данный комплекс;

4) в список литературы входят источники, с помощью которых составлялся комплекс заданий исследовательского характера. Указывается номер, автор (по алфавиту) название книг, место, издательство, страницы.

Второй этап - педагогическое проектирование (создание проекта) - дальнейшая разработка созданной модели и доведение её до уровня практического использования. При составлении комплекса подобраны задания исследовательского характера, применение которых обеспечит развитие математической грамотности у обучающихся 3 класса. Все задание имеют практический характер и предполагается самостоятельное, или совместное с учителем, сверстниками выполнение практических проб. Подобранные и классифицированные по уровням задания можно использовать на уроках, при организации индивидуальной работы.

Задания подбирались из учебников по математике, методических пособий для 3 класса и распределялись по уровням представленные в таблице (Приложение 1).

Практический этап исследования предполагает пробацию комплекса заданий исследовательского характера, направленных на развитие математической грамотности у обучающихся 3 класса.

Комплекс позволит систематизировать материал по определенной проблеме, поэтому он построен с учетом принципов: системности он предполагает, чтобы изложение учебного материала доводилось до уровня системности в создании учащихся, чтобы задания давались учащимся не только в определённой последовательности, но, чтобы они были взаимосвязанными.

Анализ ресурсов и условий реализации комплекса заданий исследовательского характера как средство развития математической грамотности младшего школьника

Комплекс заданий исследовательского характера, направленный на развитие математической грамотности у 3 класса на уроках математики будет реализован в Муниципальном казенном общеобразовательном учреждении «Вновь - Юрмытской» средней общеобразовательной школе в 3 классе. Большинство детей одного возраста - 2007 года рождения. Количество обучающихся: 15, из них мальчиков - 6, девочек - 9. Многие дети посещали детский сад, умеют общаться со сверстниками и взрослыми, знают основные правила общения, способны управлять своим поведением. В классе нет инертных и замкнутых детей, трудно контактирующих с коллективом. В целом класс активный. Дети доброжелательны, способны дружить, сопереживать друг другу.

Класс обучается по программе «Школа России». Главная идея программы: «Школа России» создается в России и для России. Школа России должна стать школой духовно-нравственного развития. Именно такая школа будет достойна России.

«Школа Росcии» - это учебно-методический комплект для 4-летней начальной школы. Научный руководитель комплекта - Андрей Анатольевич Плешаков, кандидат педагогических наук. В качестве единого целостного комплект «Школа России» работает с 2001 года. «Школа России» - это один из самых известных и востребованных учебно-методических комплектов для обучения в начальной школе. УМК постоянно обновляется и является надёжным инструментом реализации стандарта второго поколения. Ведущей целевой установкой УМК «Школа России» на протяжении всех лет было и является: «Воспитание гуманного, творческого, социально активного человека - гражданина и патриота России, уважительно и бережно относящегося к среде своего обитания, к своей семье, к природному и культурному достоянию своей малой Родины, своей многонациональной страны и всего человечества»

Для данной образовательной системы характерны следующие принципы:

1) системность. Все учебники и учебные пособия основаны на единых подходах к содержанию, сохраняют методологическое, дидактическое, психологическое и методическое единство, в них используются одни и те же основные образовательные технологии, которые, не меняясь по сути, трансформируются на каждом этапе обучения;

2) непрерывность. «Школа России» - это совокупность предметных курсов от 1 до 4 классов;

3) преемственность. Под преемственностью понимается непрерываемость на границах различных этапов или форм обучения.

Все перечисленные принципы помогают добиться желаемого результата и привить у детей интерес к обучению, а самое главное вовлечь всех обучающихся в учебную деятельность, создать эмоциональный настрой и доброжелательное отношение к каждому обучающемуся.

Основной особенностью методов и форм является то, что предпочтение отдается проблемно - поисковой и творческой деятельности младших школьников. Такой подход предусматривает создание проблемных ситуаций, выдвижение предположений, поиск доказательств, формулирование выводов, сопоставление результатов с эталоном.

В ходе подготовки к преддипломной практике осуществляется конструктивное взаимодействие с классным руководителем. Учитель предоставил все необходимые материалы студенту - практиканту для осуществления в процессе пробацию проекта.

Для реализации комплекса на практике использован метод пробации.

Пробация - это метод научного познания, направленный на выявление причинно - следственных связей и доказательства гипотезы, путем целенаправленного и контролируемого изменения условий протекания процессов или явлений.

Метод пробации предполагает достижение педагогической цели, в частности развитие у обучающихся интереса к математике. В ходе исследования у учащихся воспитываются такие качества личности, как самостоятельность, ответственность, активность, а также умение аргументировать излагать свою точку зрения, умения задавать вопросы.

Формирующая пробация предполагает активное, целенаправленное воздействие исследователя на испытуемых для того, чтобы выработать определенные свойства или качества. Кто позволит раскрыть механизмы, динамику, закономерности образования психических феноменов, определить условия их эффективного развития.

Идея пробации проекта: заключается в том, чтобы показать значимость использования комплекса заданий исследовательского характера, направленных на развитие математической грамотности у обучающихся.

Для пробации комплекса заданий исследовательского характера направленных развитие математической грамотности на уроках математики в образовательном учреждении имеются необходимые условия:

1) учебный кабинет оснащен рабочим местом учителя начальных классов, оборудованным столом, шкафами для наглядных пособий, классной доской, инструментами и приспособлениями в соответствии со спецификой обучения младших школьников;

2) учебный кабинет также оснащен техническими средствами обучения, (компьютером и мультимедийным оборудованием), учебно-наглядными пособиями, необходимыми средствами обучения для организации образовательного процесса в начальных классах. все оборудование хранится таким образом, чтобы учитель в любой момент мог быстро найти и подготовить любой предмет учебного оборудования к использованию на уроке или во внеклассной работе;

3) планировка предполагает возможность изменяться в соответствии с использованием различных форм работы;

4) в классе создан благоприятный психологический климат, комфортная среда;

5) сформировано эмоционально – положительное отношение к урочной работе;

Пространственно - временное обеспечение означает выбор оптимального места для пробирования комплекса заданий, учет влияния места на пробирование комплекса. Вводное занятие проводилось в рамках классного часа 4 апреля 2017 года. Обобщающее занятие по внедрению комплекса в образовательный процесс - 7 апреля 2017 года. Пробация заданий осуществлялась на всех проведенных уроках математики и в рамках домашнего задания. Таким образом было реализовано всего 25 заданий сборника.

Педагогические условия реализации реализации комплекса заданий исследовательского характера как средство развития математической грамотности младшего школьника

Педагогическая цель: развитие математической грамотности у обучающихся посредством заданий исследовательского характера.

Цель пробации: доказать, что реализация использования данного комплекса заданий исследовательского характера, направленного на развитие математической грамотности у обучающихся 3 класса позволяет выявить уровень математической грамотности. Следовательно, объектом пробации является процесс развития математической грамотности у обучающихся 3 класса.

Для реализации цели пробации были выдвинуты следующие задачи:

1) подобрать методики, позволяющие осуществить диагностику уровня сформированности развития математической грамотности;

2) провести первичное диагностирование обучающихся 3 класса Вновь-Юрмытской СОШ на предмет уровня сформированности математической грамотности.

3) провести пробацию комплекса заданий исследовательского характера, направленных на развитие математической грамотности у обучающихся;

4) провести вторичное диагностирование обучающихся;

5) обработать, проанализировать и интерпретировать результаты первичного и вторичного диагностического исследования.

Поставленные цели и задачи позволили сформулировать гипотезу, проверяемую в ходе пробации:

Комплекс заданий исследовательского характера, направленного на развитие математической грамотности у обучающихся, способствовал развитию математической грамотности, так как были соблюдены следующие условия:

1) включение всех учащихся в учебную деятельность;

2) установление доверительных отношений со всеми учащимися класса, основанных на взаимном уважении;

3) учет возрастных, индивидуальных особенностей, темпа работы младших школьников, типа восприятия развития внимания и памяти учащихся;

4) создание ситуации успеха для всех обучающихся через обеспечение условий работы как в зоне актуального. Так и в зоне ближайшего развития;

5) использование привлекательной и интересной для учащихся формы предъявления заданий.

Инструментарием оценки исследовательской деятельности послужили:

1) карта наблюдения на уроках математики;

2) тесты по теме (на бумажных и электронных носителях);

3) продукты деятельности учащихся в процессе изучения раздела.

Формы организации образовательного процесса:

1) фронтальная работа с классом (в основном при работе с заданиями, направленными на формирование каких – либо приемов, являющихся основными);

2) работа в группах и парах;

3) индивидуальная работа во время учебных занятий и после уроков);

4) самостоятельная работа на занятиях и дома по комплексу;

5) индивидуальные домашние задания.

Пробация созданного комплекса заданий исследовательского характера, направленного на развитие математической грамотности у обучающихся, будет способствовать развитию математической грамотности, осуществлялась в три этапа:

1) подготовительный;

2) рабочий;

3) аналитический.

На подготовительном этапе был проведен первичный замер для определения проблемного поля учащихся

Рабочий этап на данном этапе проводилась пробация созданного комплекса заданий исследовательского характера на уроках в течении четырех недель с целью выявления его действительности. На уроках математики учащимся предлагались задания исследовательского характера. Эти задания проходили либо в начале урока, либо в конце занятия.

Аналитический этап – после пробации комплекса уровень сформированности вычислительных приемов у обучающихся был еще раз исследован. Результаты были занесены в таблицу.

Состав участников исследования:

1) Исследователь: Койнова Т.Ю., студентка 4 а группы ГБПОУ «Камышловский педагогический колледж»;

2) Учащиеся 3 класса МКОУ Вновь - Юрмытская СОШ;

3) Руководитель проекта, преподаватель математических дисциплин Мадыгина Т.А.;

4) Учитель начальных классов МКОУ Вновь - Юрмытская СОШ Изюрова Н.Л.

Исследование проводилось в течении 4 недель (с 03.04по 29.04) в Свердловской области, Талицкого района в с. Вновь - Юрмытское, на базе МКОУ Вновь - Юрмытскя СОШ.

Прогноз возможных негативных последствий:

1. Реализация продукта может вызывать трудности, связанные с недостаточным уровнем развития навыков исследовательских умений у обучающихся;

2. Трудности реализации комплекса заданий исследовательского характера во внеурочной деятельности в связи с низким уровнем развития математической грамотности у младших школьников;

3. Выход за временные рамки преддипломной практики из-за нехватки времени для реализации проекта.

Способы коррекции, компенсации негативных последствий.

Чтобы избежать возможных негативных последствий необходимо:

1) проанализировать программу по математике, чтобы включить в комплекс заданий задачи уже изученные младшими школьниками.

2) подобрать интересные, разнообразные, доступные для восприятия задания;

3) заинтересовать учащихся, предложив им принять участие в олимпиаде по математике, раскрыв сущность трех данных уровней компетентности, его цели, задачи, познакомить их с инструкцией по выполнению заданий, критериями оценки;

4) создать ситуацию успеха;

5) следовать четкому плану, грамотно распределять время для подготовки;

6) согласовать планируемую в процессе пробации деятельность с классным руководителем.

Состав участников пробации:

1) обучающиеся 3 класса МКОУ Вновь-Юрмытской СОШ;

2) учителя начальных классов (осуществление экспертной оценки, выявление эффективности разработанного комплекса заданий исследовательского характера как средство развития математической грамотности);

Обязанности лиц, участвующих в пробации:

1. Учитель: своевременно и интересно реализует комплекс заданий, является организатором и наставником обучающихся.

2. Обучающиеся: являются активными участниками выполнения заданий на уроках математики и во внеурочной деятельности.

В целом можно сделать вывод о том, что цель данного комплекса достигнута задания исследовательского характера, направленные на развитие математической грамотности у обучающихся, так как показатели значительно повысились. Гипотеза доказана используя задания, направленные на формирование вычислительных приемов. Повыситься уровень математической грамотности у детей младшего школьного на достаточном уровне.

Оценка результативности комплекса заданий исследовательского характера как средство развития математической грамотности младших школьников

Пробация продукта осуществлялась на протяжении преддипломной практики в МКОУ Вновь-Юрмытской СОШ в 3 классе. В ходе прохождения практики был реализован комплекс заданий исследовательского характера, направленный на развитие математической грамотности младшего школьника.

Результатом реализации выступает развитие математической грамотности третьеклассника. На подготовительном этапе было проведён первичный замер уровня развития математической грамотности, данные наблюдения помогли выяснить уровень готовности учащихся в решении заданий исследовательского характера, данные заносились в специальную карту (Приложение 3). По результатам обработки можно сделать вывод об отрицательной динамике уровня сформированности исследовательских умений и развитии математической грамотности, так как 15% учащихся находятся на низком уровне, 25% на среднем уровне, а 60% учащихся – на высоком уровне. Свидетельством данных результатов являются такие проблемы как:

· не умение обосновать свой ответ и привести аргументы;

· затруднение в нахождении решения на тот или иной вопрос.

Анализ результатов 1 замера позволил выявить проблемное поле на устранение которого были направлены задания исследовательского характера, как средство развития математической грамотности.

Проблемное поле и пути его решения:

1) установление связей и интеграцию материала из разных математических тем, необходимого для решения поставленной проблемы;

2) недостаточный уровень развития навыков исследовательских умений у обучающихся;

3) низкий уровень развития математической грамотности у младших школьников;

Пути решения:

ü проанализировав программу по математике, я включила в комплекс задания из изученных младшими школьниками тем для повышения уровня развития математической грамотности;

ü подобрала интересные, разнообразные, доступные для восприятия задания;

ü заинтересовала учащихся, предложив им принять участие в олимпиаде по математике, раскрыв сущность трех данных уровней компетентности, его цели, задачи, познакомить их с инструкцией по выполнению заданий, критериями оценки;

На итоговом этапе был проведен 2 замер с занесением данных в карту (Приложение 5). По результатам обработки можно сделать вывод о положительной динамике уровня сформированности исследовательских умений и развитии математической грамотности, так как 10% учащихся находятся на низком уровне, 30% на среднем уровне а 60% ребят – на высоком уровне. Свидетельством данных результатов является активная включенность в предложенные виды деятельности, аргументирование собственного мнения,мобильное нахождение решения на тот или иной вопрос.

Исходя из обработанных данных можно сказать, что обучающихся с низким уровнем развития математической грамотности стало намного меньше, так как на начало практики было 60%. У учащихся, имеющих при первом замере средний уровень математической грамотности, возникали трудности в решении заданий исследовательского характера; вычислительная деятельность на занятиях не вызывала интереса, но по степени погружения в данную деятельность в рамках пробации продукта, у учащихся появилось стремление и желание находить новые способы решения задач.

Результаты первого занятия, посвященного первому уровню, включает в себя воспроизведение математических фактов, методов и выполнения вычислений, свидетельствуют о среднем, иногда и недопустимом уровне работ. Основными причинами служат неумение вычислять и воспроизводить математические факты. В конце первой недели на втором занятии учащиеся учились рассуждать и воспроизводить математические факты. С этой задачей не справились 15% учащихся. По сравнению с предыдущим занятием, количество работ, имеющих низкий уровень оценки качества уменьшилось на 5%. На последующих занятиях, дети с низким уровнем выполнения заданий отсутствуют. Наблюдается положительная динамика возрастания уровня развития математической грамотности у обучающихся. На итоговом занятии количество учащихся, имеющих высокий уровень оценки достигает 60%.

Так же при занятий, было осуществлено наблюдение за детьми. Результаты этого наблюдения занесены в карту наблюдений . По карте наблюдений можно судить, что у всех детей критерий «Диагностика развития математической грамотности младших школьников» сформировано на высоком уровне.

Комплекс заданий исследовательского характера как средство развития математической грамотности у младших школьников был опубликован на сайте «Копилка уроков», за представление проекта получила сертификат (Приложение 9).

Данные результаты доказывают, что разработанный комплекс заданий исследовательского характера является действенным средством формирования математической грамотности у обучающихся 3 класса.

Экспертами выступали учителя МКОУ Вновь - Юрмытской школы:

1. Пустозерова Людмила Анатольевна – заместитель директора, первая категория, педагогический стаж: 24 года.

2. Изюрова Надежда Леонидовна учитель начальных классов
высшая категория, педагогический стаж: 30 лет.

3. Волохина Галина Александровна учитель начальных классов
высшая категория, педагогический стаж: 27 лет.

По результатам экспертной оценки (Приложение 2) был получены следующие результаты.

Таблица 1 – результаты экспертной оценки комплекса заданий исследовательского характера как средство развития математической грамотности учащихся 3 класса

Показатели экспертной оценки	Пустозерова Л.А..	Изюрова Н.Л.	Волохина Г.А.	Средний балл	Согласованность оценок экспертов (+,-)
1. Актуальность разработки комплекса	2	2	2	2	+
2. Оформление комплекса	2	2	2	2	+
3.Содержательность комплекса	2	2	2	2	+
4.Удобство в использовании комплекса	2	2	2	2	+
Согласованность оценок экспертов (+,-)	++	++	++

По результатам экспертной оценки можно сделать выводы о том, что данный комплекс актуален и содержателен. С точки зрения рецензентов, этот комплекс будет по-настоящему полезен учителям - практикам, облегчит работу учителя начальных классов по подготовке формированию математической грамотности обучающихся. После получения экспертного заключения внесена коррекция с точки зрения его оформления.

Из методики «Диагностика интеллектуальных способностей» (Приложение 1) получен уровень общего интеллектуального развития среди обучающихся, результаты представлены (Таблица 2) «Уровни развития интеллектуальных способностей по Э.Ф.Замбицявичене».

Таким образом, анализ результатов диагностик и методик позволяет сделать вывод, что организация дополнительных занятий по математике положительно повлияла на уровень развития математической грамотности учащихся 3 класса. Результаты данной выпускной квалификационной работы были представлены на методическом объединении учителей начальных классов МКОУ Вновь-Юрмытская СОШ, так же материалы работы были опубликованы на странице интернет - проекта «Копилка уроков – сайт для учителей» (Приложение 9), и на педагогическом сайте «Готовим урок» (Приложение 10). Исходя из вышесказанного, можно сделать вывод, что разработанный комплекс заданий исследовательского характера как средство развития математической грамотности младших школьников актуален на сегодняшний день, поскольку в ходе его реализации у третьеклассников произошли положительные изменения в развитии математической грамотности.

Министерство общего и профессионального образования Свердловской области

Государственное бюджетное профессиональное образовательное учреждение

Свердловской области

«Камышловский педагогический колледж»

Камышлов, 2017

Разработала: Койнова Т.Ю., студентка 4А группы.

Руководитель: Мадыгина Т.А., преподаватель высшей квалификационной категории

Комплекс включает в себя задания исследовательского характера, направленные на развитие математической грамотности у обучающихся 3 класса. В комплекс включены содержание, пояснительная записка, проблемные задания, список литературы.

Комплекс адресован студентам педагогических колледжей, а также может быть полезен для учителей, родителей.

Оглавление

Пояснительная записка ………………………………………..………....40

Первый уровень компетентности - "Воспроизведение"……………….43

Второй уровень компетентности - "Установление связей"…………….46

Третий уровень компетентности - "Рассуждение"……………………..49

Пояснительная записка

«Функционально грамотный человек - это человек, который способен использовать все постоянно приобретаемые в течение жизни знания, умения и навыки для решения максимально широкого диапазона жизненных задач в различных сферах человеческой деятельности, общения и социальных отношений».

Леонтьев А.А.

В данном комплексе, представлены задания исследовательского характера направленные на развитие математической грамотности младших школьников.Задания могут использоваться учителями начальных классов ОУ, студентами специальности «Преподавание в начальных классах» при подготовке занятий по математике в рамках прохождения ППУ и преддипломной практики. Задания, разнообразные по содержанию и уровню, которые будут развивать математическую грамотность с помощью заданий исследовательского характера

Цель комплекса: развитие математической грамотности у обучающихся 3 классов как посредством выполнения заданий исследовательского характера.

По структуре задания делятся на задания направленные на развитие математической грамотности и оформляются с качестве уровней заданий.

Для проверки достижений первого уровня компетентности в основном предлагаются традиционные учебные задачи, характерные для проверочных работ. При этом требуется знание математических фактов, воспроизведение определений математических объектов и их свойств, применение стандартных (простых и достаточно сложных) алгоритмов и методов решения, работа с формулами, выполнение вычислений. Так как способы решения в основном стандартные, то запись самого решения не представляет интереса. В этой связи на данном уровне используются задания двух типов - с выбором ответа и с кратким свободным ответом (в виде числа, выражения, слова; решение не приводится).

Для проверки математической компетентности обучающихся используются три известных типа заданий: с выбором ответа, с кратким свободным ответом, когда ответ четко ограничен условием задачи по содержанию и форме (обычно дается в виде числа, последовательности чисел или букв, выражения, рисунка, слова и т.п.) и с развернутым свободным ответом.

Второму уровню компетентности присущи умения устанавливать связи между различными темами программы по математике и интегрировать информацию, необходимую для решения задачи. Ситуации, рассматриваемые в задачах, нестандартные, но не требующие высокого уровня математизации.

Для проверки достижения третьего уровня компетентности разрабатываются более сложные задачи, в которых, прежде всего, необходимо «математизировать» предложенную ситуацию. Эта процедура состоит из двух этапов: выделение проблемы, которая решается средствами математики, и ее формулировка, разработка соответствующей математической модели, решение и его интерпретация согласно предложенной в задании ситуации.

Данный комплекс заданий предназначен для учителей начальных классов, при проведении уроков, контрольных работ, во внеурочной деятельности, при проведении индивидуальных занятий с обучающихся, для студентов педагогических специальностей при подготовке и проведении занятий.

Первый уровень компетентности – воспроизведение.

Задания:

1.Два поезда идут навстречу друг другу со скоростями V1=36 км/ч и V2=54 км/ч. Пассажир, находящийся в первом поезде, замечает, что второй поезд проходит мимо него за t=6 мин.

Вопрос: Какова длина второго поезда?

V2=54 км/ч

2. Приготовление краски

Для того чтобы получить краску оранжевого цвета, необходимо смешать краски желтого цвета (6 частей) и красного цвета (2 части).

Вопрос: Сколько килограмм краски оранжевого цвета можно получить, имея в наличии 3 килограмма желтой и 3 килограмма красной краски?

3. Равенство

Вопрос: Как нужно расставить знаки "-", чтобы выполнялось равенство.

8 7 6 5 4 3 2 1 = 3

4.Три сотни умножили на две сотни.

Вопрос: Сколько будет сотен?

5. Диспетчер

Вы работаете диспетчером на станции «Скорая помощь». По вызову Вам необходимо отправить машину от пункта А (станция «Скорая помощь») в пункт Д по ниже приведенной схеме.

Вопрос 1:

По данной схеме выберите наиболее короткий маршрут движения машины скорой помощи от станции «Скорая помощь» (А) до пункта Д.

Подчеркните правильный ответ:

1)АКД 2)АСД 3)АЕД 4) АКЕД

Вопрос 2:

По данной схеме выберите наиболее длинный маршрут движения машины скорой помощи от станции «Скорая помощь» (А) до пункта Д.

Подчеркните правильный ответ:

1) АКЕД 2)АЕКД 3)АКЕД

6. Для приготовления обеда повару понадобилось 24 кг картошки, свеклы в 3 раза меньше, а лука в 2 раза меньше чем свеклы.

Вопрос: Сколько килограмм лука потратил повар?

7. Оля вырезала из бумаги 5 квадратов, 7 треугольников, а кругов в 2 раза больше чем треугольников.

Вопрос: Сколько всего Оля вырезала фигур?

8. Первое число 12, второе в 3 раза меньше, а третье в 4 раза больше чем второе.

Вопрос: Вычисли сумму этих трех чисел.

9. В школьную столовую привезли 6 кг, лимонов, яблок на 24 кг больше чем лимонов, а груш на 12 кг меньше чем яблок.

Вопрос: Сколько килограмм груш привезли в школьную столовую?

10. В поход пошли 24 мальчика, а девочек в 3 раза меньше, чем мальчиков. Вопрос: Сколько всего детей пошло в поход?

11. Вдоль тропинки вбиты колышки на расстоянии одного метра друг от друга. Между первым и последним колышками 8 метров.

Вопрос: Сколько всего колышков?

12. Расшифруй комбинацию кодового замка:

а) третья цифра на 3 больше, чем первая,

б ) вторая цифра на 2 больше, чем четвёртая,

в) сумма всех цифр равна 17,

г) вторая цифра 3

Вопрос: выбери правильный ответ

13. Масса поросёнка и пса 64 кг, барана и поросёнка - тоже 64 кг, а пса и барана - 60 кг.

Вопрос: Какова масса поросёнка?

14. Маугли попросил пятерых обезьян принести ему орехи. Обезьяны набрали орехов поровну и понесли Маугли. Но по дороге они поссорились, и каждая обезьяна бросила в каждую по одному ореху. В результате они принесли орехов вдвое меньше, чем собрали.

Вопрос: Сколько орехов получил Маугли?

15. В двух вагонах пригородного электропоезда ехало 65 пассажиров. На станции из первого вагона вышли 3 человека, из второго в 4 раза больше. После этого в вагонах пассажиров стало поровну.

Вопрос: Сколько пассажиров ехало в каждом вагоне до остановки?

Второй уровень компетентности – установление связей.

1. Сергей - большой любитель кататься на скейтборде. Он нередко заходит в магазин «Спорт», чтобы выяснить цены на некоторые товары. В этом магазине можно купить полностью собранный скейтборд. Нужно купить платформу, один комплект из 4 колес, один комплект из двух держателей колес, а также комплект металлических и резиновых составных частей и собрать свой собственный скейтборд.

Цены в магазине на эти товары представлены в таблице

Товар	Цена в рублях
Собранный скейтборд	82 или 84
Платформа	40, 60 или 65
Один комплект из 4 колес	14 или 36
Один комплект из 2 держателей колес	16
Один комплект металлических и резиновых деталей скейтборда (подшипники, резиновые прокладки, болты и гайки)	10 или 20

Вопрос:

Сергей хочет сам собрать для себя скейтборд. Какую наименьшую стоимость и какую наибольшую стоимость можно заплатить в этом магазине за все составные части скейтборда?

(а) Минимальная стоимость в рублях: _____________

(b) Максимальная стоимость в рублях: ____________

2.Отец с двумя сыновьями отправились в поход. На их пути встретилась река. У берега был плот, который может выдержать только отца или двух сыновей.

Вопрос: Как отцу и двум сыновьям переправиться на другой берег?

3.В район, пострадавший от землетрясения, были доставлены на грузовиках медикаменты и продовольствие: 4 грузовика с продовольствием, по 8 тонн в каждом, и столько же грузовиков с медикаментами, по 5 тонн в каждом.

Вопрос: Сколько тонн груза было доставлено в район бедствия?

4. Сын, отец и дедушка

Отцу и сыну вместе 38 лет, сыну и дедушке вместе 64 года, а отцу и дедушке вместе 84 года.

Вопрос: Сколько лет отцу, сыну и дедушке в отдельности?

5. Дарина на 5 см выше Виктории, а Виктория на 2 см ниже Ольги.

Вопрос:

1) Кто всех выше? (Дарина)?

2) Кто ниже всех? (Виктория)?

3) На сколько Дарина выше Ольги? (3см)

1. В летнем лагере ребята проходили медосмотр. Медсестра измеряла их рост. Оказалось, что Настя выше Кати на 5 см, а Маша ниже Кати на 3 см.

Вопрос: На сколько сантиметров самая высокая девочка выше самой низкой?

7 Третьеклассники участвовали в сборе макулатуры. Ученики 3 «А» класса принесли 78 кг макулатуры. Ученики 3 «Б» класса собрали на 11 кг меньше, чем ученики из 3 «А», а ученики 3 «В» класса принесли на 20 кг больше макулатуры, чем ученики из 3 «Б».

Вопрос: Сколько всего килограммов макулатуры собрали третьеклассники?

8. У мамы 2 яблока и 3 груши. Каждый день в течение 5 дней подряд она

выдает по одному фрукту.

Вопрос: Сколькими способами это может быть сделано?

9. За 3 часа работы 1 экскаватор вынул 555 м3 земли.

Вопрос: Сколько кубических метров земли вынет второй экскаватор за 4 часа, если в час он вынимает на 15 м3 больше, чем первый?

10. В лесу жили две белки – Белка и ее сестра Стрелка. Стрелка съедает на завтрак 12 орехов, а Белка на 5 меньше. На обед Стрелка съедает 14 орехов, а Белка на 4 меньше.

Вопрос: Сколько орехов они съедают за один день, если они не ужинают.

11. В каждой цепочке чисел найди закономерность и вставь пропущенные числа.

1) 3, 6, __, 12, 15, 18.

2) 1, 8, 11, 18, ___, 28, 31.

3) 2, 2, 4, 4, ___, 6, 8, 8.

4) 24, 21, ___, 15, 12.

5) 65, 60, 55, ____, 45, 40, 35.

12. Семеро детей сидят за круглым столом. Никакие 2 мальчика не сидят рядом, и никакие 3 девочки не сидят подряд.

Вопрос: Сколько девочек за столом?

13. Угадай, какие цифры обозначены буквами:

АБВГ+ АБВГ= ВГДА

14. Три девочки на вопрос, по сколько им лет ответили так: Маша: “Мне вместе с Наташей 21 год”, Наташа: “Я моложе Тамары на 4 года”, Тамара: “Нам троим вместе 34 года”.

Вопрос: Сколько лет каждой из девочек?

15. Бетти и Кетти путешествуют на суперпоезде. Бетти едет в сто семнадцатом вагоне с начала поезда, а Кетти – в сто тридцать четвертом с конца. Оказалось, что они едут в соседних вагонах.

Вопрос: Сколько вагонов могло быть в поезде?

Третий уровень компетентности - рассуждение.

1.На острове было 13 красных, 15 зеленых и 17 синих хамелеонов. Если встречаются два хамелеона разного цвета, то они одновременно меняют свой цвет на третий (например, синий и зеленый - меняются на красный).

Вопрос: Может ли случиться так, что через некоторое время все хамелеоны окажутся одного цвета?

2.В шоколадном наборе 15 одинаковых по виду конфет с тремя разными начинками, поровну с каждой начинкой.

Вопрос: Какое наименьшее число конфет надо взять, чтобы быть уверенным, что среди них есть конфеты с тремя разными начинками?

4.Имеются двое песочных часов на 3 минуты и 7 минут. Надо опустить яйцо в кипящую воду ровно на 4 минуты.

Вопрос: Как это сделать с помощью данных часов?

4. Коля, Петя и Ваня собирали грибы. Коля нашёл 10 сыроежек и столько белых, сколько подберёзовиков нашёл Ваня. Ваня нашёл лисичек в 2 раза меньше, чем сыроежек Коля, и 3 подберёзовика. Петя нашёл только лисички, которых у него больше, чем белых у Коли, но меньше, чем лисичек у Вани.

Вопрос: Сколько грибов собрали ребята, если известно, что Коля нашёл только сыроежки и белые грибы, а Ваня – подберёзовики и лисички?

5. Катя, Соня, Галя, Тамара родились 2 марта, 17 мая, 2 июня,20 марта. Соня и Галя родились в одном месяце, а у Гали и Кати дни рождения обозначались одинаковыми числами.

Вопрос: Кто какого числа и в каком месяце родился?

6. На одном заводе работали три друга: слесарь, токарь и сварщик. Их фамилии Борисов, Иванов и Семенов. У слесаря нет ни братьев, ни сестер. Он - самый младший из друзей. Семенов, женатый на сестре Борисова, старше токаря.

Вопрос: Назовите фамилии слесаря, токаря и сварщика

7. 6 спортсменов - Адамов, Белов, Ветров, Глебов, Дронов и Ершов - в проходившем соревновании заняли первые шесть мест, причем ни одно место не было разделено между ними. О том, кто какое место занял, были получены такие высказывания:

1. «Кажется, первым был Адамов, а вторым – Дронов».

2. «Нет, на первом месте был Ершов, а на втором – Глебов».

3. «Вот так болельщики! Ведь Глебов был на 3 месте, а Белов на четвертом».

4. «И вовсе было не так: Белов был пятым, а Адамов – вторым».

5. «Вы все перепутали: пятым был Дронов, а перед ним Ветров»,

Известно, что в высказывании каждого болельщика одно утверждение истинное, а второе – ложное.

Вопрос: Определить, какое место занял каждый из спортсменов.

8. Клоуны Бам, Бим и Бом вышли на арену в красной, синей и зелёной рубашках. Их туфли были тех же трёх цветов. Туфли и рубашка Бима были одного цвета. На Боме не было ничего красного. Туфли Бама были зелёные, а рубашка — нет.

Вопрос: Каких цветов были туфли и рубашки у Бома и Бима?

9. В нашем классе 30 учащихся. На экскурсию в музей ходили 23 человека, в кино и в музей - 6 человек, а 2 человека не ходили ни в кино, ни в музей.

Вопрос: Сколько человек нашего класса ходили в кино?

10. Мальчик, рост которого составлял один метр, вбил в дерево гвоздь точно на высоте своего роста. Три года спустя он вернулся на это место. Мальчик вырос на двадцать сантиметров, а дерево - на сорок сантиметров.

Вопрос: Насколько теперь гвоздь оказался выше мальчика?

11. Маша заполняет горшочек крупой. Он будет полным, если в него насыпать 6 чайных ложек, 3 десертных и 1 столовую ложку крупы или 2 чайные ложки, 1 десертную и 3 столовые ложки той же крупы. У Маши есть только столовые ложки.

Вопрос: Сколько таких ложек крупы ей придется насыпать?

12. Никита выбрал два трехзначных числа, у которых совпадают суммы цифр. От большего числа он отнял меньшее.

Вопрос: Какое самое большое число мог получить Никита?

13. Из куска проволоки согнули квадрат, площадь которого 81 кв см. Затем проволоку разогнули и согнули из неё треугольник с равными сторонами.

Вопрос: Какова длина стороны полученного треугольника?

14. Серёжа задумал число, прибавил к нему 8,от результата отнял 5 и получил 3.

Вопрос: Какое число он задумал?

15. В пятиэтажном доме Вера живёт выше Пети, но ниже Славы, а Коля живёт ниже Пети.

Вопрос: На каком этаже живёт Вера, если Коля живёт на втором этаже?

Список литературы

1. Антоненко, ‏ㅤТ. ‏ㅤЕ. ‏ㅤПриемы ‏ㅤзанимательности ‏ㅤна ‏ㅤуроках ‏ㅤматематики ‏ ‏ㅤ/ ‏ㅤТ. ‏ㅤЕ. ‏ㅤАнтоненко ‏ㅤ// ‏ㅤНачальная ‏ㅤшкола. ‏ㅤ2008. ‏ㅤ№4 ‏ㅤ

2. Антонов, ‏ㅤД. ‏ㅤА. ‏ㅤРазвитие ‏ㅤтворческой ‏ㅤактивности ‏ㅤучащихся ‏ㅤпри ‏ㅤработе ‏ㅤнад ‏ㅤматематическим ‏ㅤтекстом. ‏ㅤ/ ‏ㅤД. ‏ㅤА. ‏ㅤАнтонов ‏ㅤ// ‏ㅤМатематика ‏ㅤв ‏ㅤшколе. ‏ㅤ1980. ‏ㅤ№3. ‏ㅤ

3. Беспалько, ‏ㅤВ. ‏ㅤП. ‏ㅤОсновы ‏ㅤтеории ‏ㅤпедагогических ‏ㅤсистем. ‏ㅤ‏ㅤ/ ‏ㅤВ. ‏ㅤП. ‏ㅤБеспалько ‏ㅤ// ‏ㅤВоронеж, ‏ㅤ1977. ‏ㅤ

4. Блонский, ‏ㅤП. ‏ㅤП. ‏ㅤПамять ‏ㅤи ‏ㅤмышление. ‏ ‏ㅤ/ ‏ㅤП. ‏ㅤП. ‏ㅤБлонский ‏ㅤ// ‏ㅤСанкт-Петербург ‏ㅤ// ‏ㅤ2001. ‏ㅤ

5. Бостоногова, ‏ㅤЛ. ‏ㅤП. ‏ㅤТворческие ‏ㅤзадания ‏ㅤдля ‏ㅤдетей ‏ㅤ6 ‏ㅤлет. ‏ㅤ‏ㅤ/Л. ‏ㅤП. ‏ㅤБостоногова ‏ㅤ// ‏ㅤНачальная ‏ㅤшкола. ‏ㅤ2005. ‏ㅤ№4 ‏ㅤ

6. Братанова, ‏ㅤТ. ‏ㅤА. ‏ㅤМетодика ‏ㅤорганизации ‏ㅤигр-исследований ‏ㅤс ‏ㅤмладшими ‏ㅤшкольниками ‏ㅤㅤ/ ‏ㅤТ. ‏ㅤА. ‏ㅤБратанова ‏ㅤ// ‏ㅤНачальная ‏ㅤШкола. ‏ㅤ2008. ‏ㅤ№ ‏ㅤ5.

7. Буряк, ‏ㅤВ. ‏ㅤК. ‏ㅤСамостоятельная ‏ㅤработа ‏ㅤучащихся. ‏ㅤ/ ‏ㅤВ. ‏ㅤК. ‏ㅤБуряк ‏ㅤ// ‏ㅤМ., ‏ㅤ1984. ‏ㅤ

8. Горшкова, ‏ㅤО. ‏ㅤД. ‏ㅤНачальная ‏ㅤшкола: ‏ㅤматематика: ‏ㅤнестандартные ‏ㅤзадания. ‏ㅤ1-4 ‏ㅤклассы. ‏ㅤㅤ/ ‏ㅤО. ‏ㅤД. ‏ㅤГоршкова ‏ㅤ// ‏ㅤ2005. ‏ㅤ

9. Далингер, ‏ㅤВ. ‏ㅤА. ‏ㅤУчебно-исследовательская ‏ㅤдеятельность ‏ㅤучащихся ‏ㅤв ‏ㅤпроцессе ‏ㅤизучения ‏ㅤматематики / ‏ㅤ«Вестник ‏ㅤОмского ‏ㅤгосударственного ‏ㅤпедагогического ‏ㅤуниверситета», ‏ㅤ2007. ‏ㅤ

10. Дебашина, ‏ㅤЕ. ‏ㅤЮ. ‏ㅤСамостоятельная ‏ㅤработа ‏ㅤна ‏ㅤуроках ‏ㅤматематики ‏ㅤв ‏ㅤусловиях ‏ㅤразвивающего ‏ㅤобучения ‏ㅤ/ ‏ㅤЕ. ‏ㅤВ. ‏ㅤДебашина ‏ㅤ// ‏ㅤНачальная ‏ㅤшкола. ‏ㅤ2003. ‏ㅤ№ ‏ㅤ7. ‏ㅤ

Список литературы

7. Буряк, ‏ㅤВ. ‏ㅤК. ‏ㅤСамостоятельная ‏ㅤработа ‏ㅤучащихся. ‏ㅤ/ ‏ㅤВ. ‏ㅤК. ‏ㅤБуряк ‏ㅤ// ‏ㅤМ., ‏ㅤ1984. ‏ㅤ

11. Демидова, ‏ㅤТ. ‏ㅤЕ., ‏ㅤКозлова, ‏ㅤС. ‏ㅤА., ‏ㅤТонких, ‏ㅤА. ‏ㅤП. ‏ㅤМоя ‏ㅤматематика: ‏ㅤУчебники ‏ㅤдля ‏ㅤ1-4 ‏ㅤклассов. ‏ ‏ㅤМ. Баласс, ‏ㅤ2005.

12. Демидова, ‏ㅤТ. ‏ㅤЕ., ‏ㅤКозлова, ‏ㅤС. ‏ㅤА., ‏ㅤТонких, ‏ㅤА. ‏ㅤП. ‏ㅤРабочая ‏ㅤтетрадь ‏ㅤк ‏ㅤучебнику ‏ㅤ«Моя ‏ㅤматематика». ‏ㅤМ. ‏ㅤБаласс, ‏ㅤ2005.

13. Дзанагова, ‏ㅤР. ‏ㅤМ. ‏ㅤРаскрытие ‏ㅤтворческих ‏ㅤспособностей ‏ㅤучеников. ‏ㅤㅤ/Р. ‏ㅤМ. ‏ㅤДзанагова ‏ㅤ// ‏ㅤНачальная ‏ㅤшкола. ‏ㅤ2007. ‏ㅤ№6 ‏ㅤ. ‏ㅤ

14. Зак, А.З. Развитие интеллектуальных способностей у детей 6-7 лет: Учебно-методическое пособие для учителей. – М.: Новая школа, 1996.

15. Зак, А.З. Развитие интеллектуальных способностей у детей 8 лет: Учебно-методическое пособие для учителей. – М.: Новая школа, 1996.

16. Зак, А.З. Развитие интеллектуальных способностей у детей 9 лет: Учебно-методическое пособие для учителей. – М.: Новая школа, 1996.

17. Ивашова, ‏ㅤО. ‏ㅤА. ‏ㅤРоль ‏ㅤисследовательской ‏ㅤдеятельности ‏ㅤмладших ‏ㅤшкольников ‏ㅤв ‏ㅤовладении ‏ㅤматематической ‏ㅤкультурой ‏ㅤ‏ㅤ// ‏ㅤ«Культ-Информ-Пресс», ‏ㅤ2003. ‏ㅤ

18. Кларин, ‏ㅤМ. ‏ㅤВ. ‏ㅤИнновации ‏ㅤв ‏ㅤмировой ‏ㅤпедагогике: ‏ㅤобучение ‏ㅤна ‏ㅤоснове ‏ㅤисследования. ‏‏ㅤ- ‏ㅤРига, ‏ㅤ«Эксперимент».

19. Комарова, ‏ㅤИ. ‏ㅤВ. ‏ㅤОрганизация ‏ㅤучебно-исследовательской ‏ㅤдеятельности ‏ㅤв ‏ㅤначальной ‏ㅤшколе ‏ㅤ(доклад, ‏ㅤРегиональная ‏ㅤконференция ‏ㅤпединициатив ‏ㅤ2007) ‏ㅤ// ‏ㅤПетрозаводск, ‏ㅤ2007

20. Кордемский, ‏ㅤБ. ‏ㅤА. ‏ㅤМатематическая ‏ㅤсмекалка. ‏ㅤ‏ㅤМ., ‏ㅤ1955. ‏ㅤ

21. Крутецкий, ‏ㅤВ. ‏ㅤА. ‏ㅤПсихология ‏ㅤматематических ‏ㅤспособностей ‏ㅤшкольников. ‏ㅤ/ ‏ㅤВ. ‏ㅤА. ‏ㅤКрутецкий ‏ㅤ// ‏ㅤㅤМ.; ‏ㅤВоронеж. ‏ㅤ1998. ‏ㅤ

22. Ляхова, ‏ㅤЛ. ‏ㅤВ. ‏ㅤОрганизация ‏ㅤнаучно-исследовательской ‏ㅤдеятельности ‏ㅤучащихся. ‏ㅤㅤ/Л. ‏ㅤВ. ‏ㅤЛяхова ‏ㅤ// ‏ㅤНачальная ‏ㅤшкола. ‏ㅤ2009. ‏ㅤ№7. ‏ㅤ

23. Магомедов, ‏ㅤН. ‏ㅤГ. ‏ㅤНекоторые ‏ㅤупражнения ‏ㅤпо ‏ㅤусвоению ‏ㅤэлементов ‏ㅤматематической ‏ㅤлогики ‏ㅤㅤ/Н. ‏ㅤГ. ‏ㅤМагомедв ‏ㅤ//Начальная ‏ㅤшкола. ‏ㅤ2002. ‏ㅤ№ ‏ㅤ3. ‏ㅤ

24. Орлова, ‏ㅤЛ. ‏ㅤА. ‏ㅤУчастие ‏ㅤмладших ‏ㅤшкольников ‏ㅤв ‏ㅤпроектно-исследовательской ‏ㅤработе. ‏ㅤㅤ/ ‏ㅤЛ. ‏ㅤА. ‏ㅤОрлова ‏ㅤ// ‏ㅤНачальная ‏ㅤшкола. ‏ㅤ2007. ‏ㅤ№3. ‏ㅤ

25. Пакет ‏ㅤприкладных ‏ㅤпрограмм ‏ㅤ«Кирилл ‏ㅤи ‏ㅤМефодий».

26. Национальная ‏ㅤобразовательная ‏ㅤинициатива ‏ㅤ«Наша ‏ㅤновая ‏ㅤшкола», ‏ㅤприказом ‏ㅤМинистерства ‏ㅤобразования ‏ㅤи ‏ㅤнауки ‏ㅤРоссийской ‏ㅤФедерации ‏ㅤот ‏ㅤ« ‏ㅤ6 ‏ㅤ» ‏ㅤоктября ‏ㅤ2009 ‏ㅤг. ‏ㅤ№ ‏ㅤ37

27. Пержинская, ‏ㅤЕ. ‏ㅤВ. ‏ㅤКак ‏ㅤорганизовать ‏ㅤисследовательскую ‏ㅤработу ‏ㅤв ‏ㅤ1 ‏ㅤклассе. ‏‏ㅤ/ ‏ㅤЕ. ‏ㅤВ. ‏ㅤПержинская ‏ㅤ// ‏ㅤНачальная ‏ㅤшкола. ‏ㅤ2008. ‏ㅤ№ ‏ㅤ5. ‏ㅤ

28. Пичугин, ‏ㅤС. ‏ㅤС. ‏ㅤУчебно-исследовательская ‏ㅤдеятельность ‏ㅤмладших ‏ㅤшкольников ‏ㅤна ‏ㅤуроках ‏ㅤматематики ‏ㅤ/ ‏ㅤС. ‏ㅤС. ‏ㅤПичугин ‏ㅤ//Начальная ‏ㅤшкола. ‏ㅤ2008. ‏ㅤ№6. ‏ㅤ

29. Семёнова, ‏ㅤН. ‏ㅤА. ‏ㅤИсследовательская ‏ㅤдеятельность ‏ㅤучащихся. ‏ㅤㅤ/Н. ‏ㅤА. ‏ㅤСеменов ‏ㅤ// ‏ㅤНачальная ‏ㅤшкола. ‏ㅤ2006. ‏ㅤ№2. ‏ㅤ

30. Савенков, ‏ㅤА. ‏ㅤИ. ‏ㅤМетодика ‏ㅤисследовательского ‏ㅤобучения ‏ㅤмладших ‏ㅤшкольников. ‏ㅤ/А. ‏ㅤИ. ‏ㅤСавенков ‏ㅤ// ‏ㅤМ.: ‏ㅤИзд. ‏ㅤдом ‏ㅤ«Федоров». ‏ㅤ2006. ‏ㅤ

31. Савенков, ‏ㅤА. ‏ㅤИ. ‏ㅤПсихология ‏ㅤисследовательского ‏ㅤобучения. ‏ㅤㅤ/ ‏ㅤА. ‏ㅤИ. ‏ㅤСавенков ‏ㅤ// ‏ㅤМосква, ‏ㅤАкадемия ‏ㅤразвития. ‏ㅤ2005 ‏ㅤг. ‏ㅤ

32. Савенков, ‏ㅤА. ‏ㅤИ. ‏ㅤПсихологические ‏ㅤосновы ‏ㅤисследовательского ‏ㅤподхода ‏ㅤк ‏ㅤобучению. ‏ㅤ/ ‏ㅤА. ‏ㅤИ. ‏ㅤСавенков ‏ㅤ// ‏ㅤМ., ‏ㅤ2006. ‏ㅤ

33. Смирнова, ‏ㅤА. ‏ㅤА. ‏ㅤМетод ‏ㅤварьирования ‏ㅤтекстовых ‏ㅤзадач ‏ㅤпо ‏ㅤматематике ‏ㅤкак ‏ㅤсредство ‏ㅤповышения ‏ㅤкачества ‏ㅤзнаний ‏ㅤучащихся: ‏ㅤДис. ‏ㅤ... ‏ㅤканд. ‏ㅤпед. ‏ㅤнаук. ‏ㅤ/ ‏ㅤА. ‏ㅤА. ‏ㅤСмирнов ‏ㅤ// ‏ㅤСПб., ‏ㅤ2007.

34. Смолкина, ‏ㅤЕ. ‏ㅤВ. ‏ㅤИсследовательская ‏ㅤдеятельность ‏ㅤучащихся ‏ㅤкак ‏ㅤсредство ‏ㅤреализации ‏ㅤличности ‏ㅤв ‏ㅤобщеобразовательном ‏ㅤпространстве. ‏ㅤ/ ‏ㅤЕ. ‏ㅤВ. ‏ㅤСмолкина ‏ㅤ// ‏ㅤНачальная ‏ㅤшкола. ‏ㅤ2007. ‏ㅤ№2. ‏ㅤ

35. Тимофеева, ‏ㅤВ. ‏ㅤП. ‏ㅤИсследовательская ‏ㅤработа ‏ㅤв ‏ㅤначальной ‏ㅤшколе. ‏ ‏ㅤ/ ‏ㅤВ. ‏ㅤП. ‏ㅤТимофеева ‏ㅤ// ‏ㅤНачальная ‏ㅤшкола. ‏ㅤ2008. ‏ㅤ№2. ‏ㅤ

36. Тихонова, ‏ㅤН. ‏ㅤБ., ‏ㅤТрошина ‏ㅤТ. ‏ㅤС. ‏ㅤОбучение ‏ㅤсоставления ‏ㅤэвристических ‏ㅤалгоритмов ‏ㅤкак ‏ㅤспособ ‏ㅤразвития ‏ㅤтворческих ‏ㅤспособностей ‏ㅤмладших ‏ㅤшкольников. ‏ㅤ/Н.Б. ‏ㅤТихонова// ‏ㅤНачальная ‏ㅤшкола ‏ㅤДо ‏ㅤи ‏ㅤПосле. ‏ㅤ2004. ‏ㅤ№9.

37. Тупичкина, ‏ㅤЕ.А., ‏ㅤВиды ‏ㅤсамостоятельных ‏ㅤработ ‏ㅤна ‏ㅤуроках ‏ㅤматематики ‏ㅤ// ‏ㅤТупичкина ‏ㅤЕ.А., ‏ㅤКрючкова ‏ㅤИ.В. ‏ㅤ// ‏ㅤНачальная ‏ㅤшкола. ‏ㅤ1996. ‏ㅤ№ ‏ㅤ5. ‏ㅤ

38. Федеральный ‏ㅤГосударственный ‏ㅤОбразовательный ‏ㅤСтандарт ‏ㅤНачального ‏ㅤОбщего ‏ㅤОбразования/Утверждаю ‏ㅤПрезидент ‏ㅤРоссийской ‏ㅤФедерации ‏ㅤД.Медведев

39. Ямалтдинова ‏ㅤД. ‏ㅤГ. ‏ㅤОрганизация ‏ㅤсамостоятельной ‏ㅤдеятельности ‏ㅤучащихся ‏ㅤㅤ/Д.Г.Ямалтдинова// ‏ㅤНачальная ‏ㅤшкола. ‏ㅤ2008. ‏ㅤ№2. ‏ㅤ

40. Ямалтдинова ‏ㅤД. ‏ㅤГ ‏ㅤОрганизация ‏ㅤсамостоятельной ‏ㅤтворческой ‏ㅤдеятельности ‏ㅤмладших ‏ㅤшкольников ‏ㅤна ‏ㅤуроках ‏ㅤматематики ‏‏ㅤ/ ‏ㅤД. ‏ㅤГ. ‏ㅤЯмалтдинова ‏ㅤ// ‏ㅤНачальная ‏ㅤшкола ‏ㅤДо ‏ㅤи ‏ㅤПосле. ‏ㅤ2007. ‏ㅤ№10. ‏ㅤ

41. Швецова Р.Ф. Самостоятельная работа на уроках математики в начальной школе // Начальная школа плюс до и после. 2013. № 10.

42. Царёва, С.Е. Методика преподавания математики в начальной школе: учебник для студентов учреждений высшего образования / С.Е. Царёва. – Москва: Издательский центр «Академия», 2014.

43. Примерная основная образовательная программа образовательного учреждения. Начальная школа / [сост. Е.С.Савинов]. – 4-е изд., перераб. – М.: Просвещение, 2013.

44. Моро М.И., Волкова С.И., Степанова С.В. учебник «Математика» 1 класс (1,2 часть), УМК «Школа России»: Просвещение, 2011.;

45. Мир детства: Младший школьник. - М.: Педагогика. 2003.

46. Дорофеев, Г.В., Миракова, Т.Н. Математика. Учебник для 1 класса начальной школы в двух частях /Г.В.Дорофеев М.: Просвещение, 2007г.;

47. Дмитриев Д.В. Толковый словарь русского языка. URL: http://onlineslovari.com/tolkovyiy_slovar_dmitrieva/ (дата обращения: 30.09.16)

48. Бордовская Н.В. Педагогика: учебное пособие. /Н.В.Бордовская, А.А.Реан. – Гриф МО. – СПб.: Питер, 2008.;

49. Бантова М. А., Бельтюкова Г. В. Методика преподавания математики в начальных классах. Москва. "Просвещение". 1984г.;

50. Примерная программа по математике; руководители проекта: президент РАО Н.Д. Никандров, М.В. Рыжаков, А.М. Кондаков; Просвещение. 2010 (Стандарт второго поколения);

Приложение 1

Методика №1. Методика диагностики интеллектуальных способностей

Одной из вербальных методик диагностики интеллектуальных способностей является методика Э.Ф. Замбицявичене.

Тест состоит из четырех субтестов, включающих в себя вербальные задания.

Первый субтест направлен на исследование дифференциации существенных признаков предметов и явлений от несущественных, а также запаса знаний испытуемого (способность анализировать).

Второй субтест направлен на исследование способности группировать предметы и явления по существенным признакам, а также операций обобщения и отвлечения (способность классифицировать).

Третий субтест направлен на исследование способности устанавливать логические связи и отношения между понятиями (способность рассуждать).

Четвертый субтест направлен на выявление умения обобщать (способность к обобщению).

Каждый субтест состоит из 10 заданий. Каждое задание в зависимости от степени сложности оценивается от 1,9 до 3,4 балла. Суммировав результаты всех субтестов, получим уровень общего интеллектуального развития.

Путем обработки полученных результатов можно получить классификацию коэффициентов интеллектуальных способностей, которая представлена в таблице № 2.

Уровни развития интеллектуальных способностей по Э.Ф.Замбицявичене

Таблица 2

№ субтеста	Количество баллов	Уровень развития интеллектуальных способностей
1	20-26	Высокий
	13-19	Средний
	12 и ниже	Низкий
2	20-26	Высокий
	13-19	Средний
	12 и ниже	Низкий
3	17-23	Высокий
	11-17	Средний
	10 и ниже	Низкий
4	19-25	Высокий
	12-18	Средний
	11 и ниже	Низкий
Общий уровень	75-100	Высокий
	50-74	Средний
	49 и ниже	Низкий

Диагностика может применяться как для индивидуального, так и для группового исследования. Однако индивидуальное исследование предпочтительней, поскольку оно дает наиболее полную информацию об испытуемом. Поэтому исследовали испытуемых индивидуально. Каждому из них были предложены задания по всем субтестам методики.

Приложение 2

ЛИСТ ЭКСПЕРТНОЙ ОЦЕНКИ

комплекса заданий исследовательского характера как средство развития математической грамотности у младшего школьника

Ф.И.О. эксперта: _________________________________ОУ____________________

должность_________________________КК______________________Пед.стаж_______

Критерии оценки: 0 – признак не проявляется, 1 – признак проявляется частично, 2 – признак проявляется в полной мере

Шкала перевода среднего балла в уровень: 1,7 – 2 – высокий уровень;

1 – 1,6 – средний уровень; 0,5 – 0,9 – низкий уровень; 0– 0,4 – недопустимый уровень.

Показатели экспертной оценки	Оценка Эксперта
1.Актуальность комплекса 1.1 Аргументированность выбора проблемы, соответствие ФГОС НОО 1.2 Научность 1.3 Новизна
2. Оформление комплекса 2.1 Структурированность (отражены все компоненты комплекса) 2.2 Оформление всех частей комплекса в соответствии с требованиями
3. Содержательность комплекса 3.1 Содержательная обоснованность созданного комплекса в пояснительной записке (актуальность, цель и задачи комплекса, обоснование структуры и содержания сборника) 3.2 Ориентированность заданий на актуальные аспекты развития математической грамотности 3.3 Соответствие заданий возрастным особенностям детей 3.4 Соответствие заданий УМК 3.5 Направленность на решение проблем
4. Удобство в использовании комплекса
Общая оценка показателей экспертной оценки (сумма баллов)
Средняя оценка показателей экспертной оценки, уровень

Общие выводы, рекомендации

Подпись эксперта______________( )

Подпись руководителя ОУ________________( )М.П.

Приложение 3

Результаты диагностики уровня развития математической грамотности младших школьников

(первичный замер, 07.04.2017)

Цель: определение развития математической грамотности младших школьников.

Процедура обследования: респонденту необходимо решить несколько заданий из комплекса, которые оцениваются по шкале.

Критерии оценки: 2балла - показатель проявляется оптимально (высокий); 1 балл – показатель проявляется частично (средний); 0 баллов - показатель не появляется (низкий).

Таблица 3

Критерии	Респонденты															Средний балл
Критерии	№ 1	№ 2	№ 3	№ 4	№ 5	№ 6	№ 7	№ 8	№ 9	№ 10	№ 11	№ 12	№ 13	№ 14	№ 15	Средний балл
1. умение выполнять математические расчеты для решения повседневных задач;	1	1	2	1	1	2	1	1	2	1	1	1	2	1	1	1,2
2. умение рассуждать, делать выводы на основе информации, представленной в различных формах	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1
3. распознавать проблемы, возникающие в окружающей действительности и которые можно решить средствами математики;	2	2	1	2	1	1	2	2	2	1	1	1	1	1	1	1,4
4. формулировать эти проблемы на языке математики;	1	0	1	1	0	1	2	1	1	1	0	0	1	1	1	0,8
5. решать эти проблемы, используя математические факты и методы;	2	2	2	1	1	1	1	1	1	1	2	1	1	1	2	1,3
6. анализировать использованные методы решения;	1	1	1	1	1	0	1	1	0	0	1	1	1	1	1	0,8
7. интерпретировать полученные результаты с учетом поставленной проблемы;	1	1	1	1	0	1	2	0	0	1	1	0	1	1	2	0,86
Итоговый ср.балл	1	1,1	1,3	1,1	0,8	1	1,3	1,1	1,1	0,8	1	0,8	1,1	1	1,1	1,04

Приложение 4

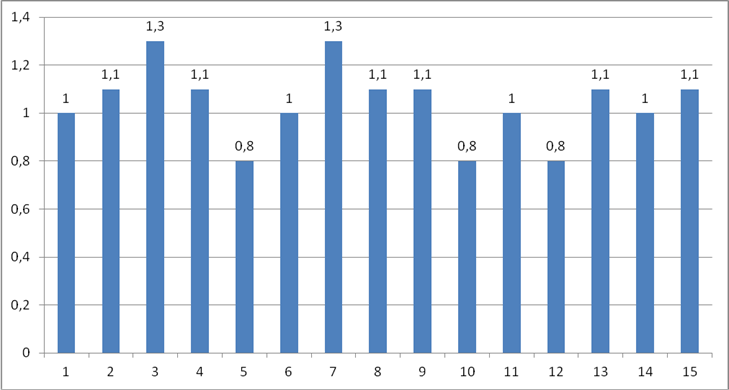
Рисунок 1 - Результаты диагностики уровня развития математической грамотности младших школьников

(первичный замер, 07.04.2017)

Критерии оценивания: показатель проявился в полной мере - 2 балл; показатель проявился при частичном присутствии - 1 балла; показатель не проявлен - 0 баллов

Шкала перевода: 1,8-2 баллов – высокий уровень, 1,4-1,7 баллов – средний уровень, 1-1,3 балла – низкий уровень, менее 1 балла – недопустимый уровень

По результатам диагностики развития математической грамотности младших школьников продемонстрирован уровень сформированности у детей математической грамотности на 1 замер. Исходя из проведенной диагностики, можно сделать вывод о том, что у обучающихся на высоком уровне продемонстрированы такие умения как:

На высоком уровне:

· распозновать проблемы, возникающие в окружающей действительности и которые можно решить средствами математики;

· решать эти проблемы, используя математические факты и умения.

На среднем уровне выявлены такие умения как:

· формулировать эти проблемы на языке математики;

· интепретировать полученные результаты с учетом поставленной проблем.

На низком уровне:

· умение рассуждать, делать выводы на основе информации, представленной в различных формах;

· анализировать использованные методы решения;

Приложение 5

Результаты диагностики уровня развития математической грамотности младших школьников

(вторичный замер, 21.04.2017)

Цель: определение развития математической грамотности младших школьников.

Таблица 4

Критерии	Респонденты															Средний балл
Критерии	№ 1	№ 2	№ 3	№ 4	№ 5	№ 6	№ 7	№ 8	№ 9	№ 10	№ 11	№ 12	№ 13	№ 14	№ 15	Средний балл
1. умение выполнять математические расчеты для решения повседневных задач;	1	1	2	1	1	2	1	1	2	1	1	1	2	1	1	1,2
2. умение рассуждать, делать выводы на основе информации, представленной в различных формах	1	1	1	1	1	1	1	1	1	1	1	2	1	1	2	1,1
3. распознавать проблемы, возникающие в окружающей действительности и которые можно решить средствами математики;	2	2	1	2	1	1	2	2	2	1	2	2	1	2	1	1,6
4. формулировать эти проблемы на языке математики;	1	0	1	1	0	1	2	1	1	1	0	0	1	1	1	0,8
5. решать эти проблемы, используя математические факты и методы;	2	2	2	1	1	1	1	1	1	1	2	1	1	1	2	1,3
6. анализировать использованные методы решения;	1	1	1	1	1	0	1	1	0	0	1	1	1	1	1	0,8
7. интерпретировать полученные результаты с учетом поставленной проблемы;	1	1	1	1	1	1	2	1	0	1	1	0	1	1	2	1
Итоговый ср.балл	1,2	0,8	1,2	1,1	0,8	1	1,4	1,1	1	0,8	1,1	1	1,1	1,1	1,4	1,1

Приложение 6

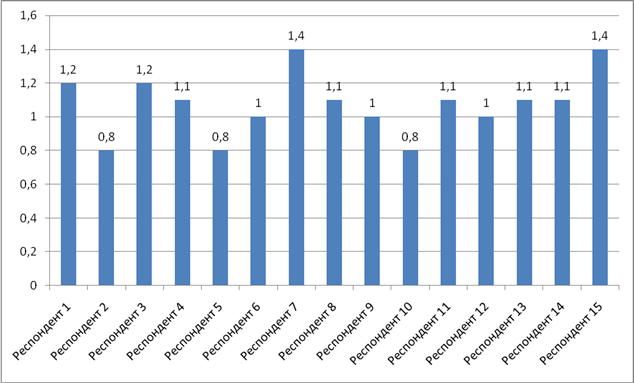
Рисунок 2 - Результаты диагностики уровня развития математической грамотности младших школьников

(вторичный замер, 21.04.2017)

По результатам диагностики развития математической грамотности младших школьников продемонстрирован уровень сформированности у детей математической грамотности на 2 замер. Исходя из проведенной диагностики, можно сделать вывод о том, что у обучающихся продемонстрированы такие умения как:

На высоком уровне:

· решать эти проблемы, используя математические факты и умения;

· интепретировать полученные результаты с учетом поставленной проблем.

На среднем уровне выявлены такие умения как:

· формулировать эти проблемы на языке математики;

На низком уровне:

· умение рассуждать, делать выводы на основе информации, представленной в различных формах;

· анализировать использованные методы решения;

Приложение 7

В ходе решения заданий обучающиеся продемонстрируют знания того, на сколько они понимают задания тех уровней компетентности, которые представлены в самом комплексе. Это видно из таблицы №5.

Таблица №5

Высокий уровень

Учащиеся демонстрируют:

- умения выполнять решение многошаговых текстовых задач, требующих проведения вычислений с натуральными числами;

- способности определения зависимости между данными парами чисел;

- умение рассуждать и воспроизводить математические факты.

Средний уровень

Учащиеся умеют и способны:

- применять базовые математические знания в простых ситуациях с четко поставленным прямым вопросом;

- прочитать, проинтерпретировать и использовать различные представления чисел;

Низкий уровень

Учащиеся демонстрируют:

- некоторые базовые знания;

- понимание сложения и вычитания натуральных чисел;

Приложение 8

Контрольная работа по математике на выявление развитие математической грамотности

Цель: проверить усвоение:

1) вычислительных приемов сложения, вычитания в пределах 100;

2) правил порядка выполнения действий в выражениях;

3) единиц длины;

4) умения решать простые задачи и составные разными способами.

5) умение делать выводы и на основании этих выводов продолжать решение.

Задания составлены с опорой на логические приёмы: сравнение, обобщение, выделение существенных признаков, классификация.

1. А). Поставь вопрос к задаче и реши её.

На новогодней ёлке висело 18 красных шаров и 12 зелёных.

Б). Поставь к задаче другой вопрос и реши её.

2. А). Найди значения выражений: 27+39 28+37 29+35

Б). Найди закономерность и продолжи ряд ещё 3 равенствами.

3. А). Запиши отрезок натурального ряда из семи чисел, последнее из которых 13.

Б). Запиши отрезок натурального ряда из семи чисел, меньших 13.

Постарайся найти несколько решений.

4. А). Начерти незамкнутую ломаную линию со звеньями длиной 4 см, 3см, 2см и 5см.

Б). Начерти незамкнутую ломаную линию такой же длины, но с другими звеньями.

Приложение 9

Приложение 10

Выпускная квалификационная работа Комплекс заданий исследовательского характера как средство развития математической грамотности младших школьников

Материалы на данной страницы взяты из открытых истончиков либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.

08.12.2019