Выступление на МО учителей математике по теме "Современные образовательные технологии на уроках математики"

МОУ «Крутоярская СОШ»

Современные образовательные технологии на уроках математики

Учитель математики: Каптилова В.А.

Крутоярский, 2024

Среди главных задач современного образования – адаптация учащегося к жизни, привитие ему навыков самообразования, творческого использования полученных знаний. В условиях ФГОС, в которых описано не только содержание, но и требования к результатам обучения.  Образование требует инновационных подходов в организации учебного процесса.

       «Педагогическая технология – это продуманная во всех деталях модель совместной педагогической деятельности по проектированию, организации и проведению учебного процесса с безусловным обеспечением комфортных условий для учащихся и учителя» (В.М. Монахов).

Признаки, присущие педагогической технологии:

·        Концептуальность (научная база): каждой педагогической технологии должна быть присуща опора на определенную научную концепцию, научное обоснование достижения образовательных целей.

·        Системность: педагогическая технология должна обладать всеми признаками системы: логикой процесса; взаимосвязью всех его частей; целостностью.

·        Управляемость: возможность диагностичного целеполагания; планирования; проектирования процесса обучения; поэтапной диагностики; варьирования средствами и методами с целью коррекции результатов.

·        Эффективность по результатам и оптимальность по затратам, гарантированность достижения запланированных результатов обучения в сжатые сроки.

·        Воспроизводимость (алгоритмируемость, проектируемостъ, целостность, управляемость) – возможность применения педагогической технологии в других однотипных образовательных учреждениях, другими субъектами.

·        Корректируемостъ – возможность постоянной оперативной обратной связи.

Для реализации познавательной и творческой активности школьников учебном процессе используются современные образовательные технологии.      Современные  образовательные   технологии   способствуют   повышению, качества образования, ориентированы на индивидуализацию, дистанционность и    вариативность   образовательного   процесса,   академическую   мобильность обучаемых, независимо от возраста и уровня образования.

В школе представлен широкий спектр образовательных педагогических технологий, которые применяются в учебном процессе. В условиях реализации требований ФГОС ООО наиболее актуальными становятся технологии:

·        Информационно–коммуникационная технология

·        Проектная технология

·        Технология развивающего обучения

·        Здоровьесберегающие технологии

·        Игровые технологии

·        Модульная технология

·        Технология мастерских

·          Кейс–технология

·        Технология интегрированного обучения

·        Педагогика сотрудничества.

·        Технологии уровневой дифференциации

·          Групповые технологии.

·        Традиционные технологии (классно-урочнаясистема) Рассмотрим некоторые виды технологий на уроках математики:

Информационно-коммуникативная технология.

Информационные технологии могут быть использованы на различных этапах урока математики:

·         Самостоятельное обучение с отсутствием или отрицанием деятельности учителя;

·         Частичная замена (фрагментарное,выборочноеиспользование дополнительного материала);

·         Использование тренировочных программ;

·         Выполнение домашних самостоятельных и творческих заданий;

·         Использование компьютера для вычислений, построения графиков;

·         Использование информационно – справочных программ.

Урок с использованием информационных технологий становится более наглядным для учащихся, появляется мотивация к изучению предмета. Использование некоторых компьютерных программ позволяет облегчить труд педагога: графика и мультипликация помогает ученикам понимать сложные логические математические построения, подбор заданий, тестов, проверка и оценка качества знаний, тем самым на уроке освобождается время для дополнительных заданий (за счет того, что материалы заранее заготовлены в электронном виде).

Информационные технологии предоставляют широкие возможности для индивидуализации и дифференциации обучения, причем не только за счет разноуровневых заданий, но также и за счёт самообразования учащегося.

Формы использования ИКТ

В процессе преподавания математики, информационные технологии могут использоваться в различных формах. Используемые мною направления можно представить в виде следующих основных блоков:

·         Мультимедийные сценарии уроков;

·         проверка знаний на уроке и дома (самостоятельные работы, математические диктанты, контрольные и самостоятельные работы, онлайн тесты);

·         подготовка к ОГЭ,ЕГЭ

Технология развития критического мышления.

Критическое мышление – это способность анализировать информацию с помощью логики и личностно-психологического подхода, с тем, чтобы применять полученные результаты как к стандартным, так и нестандартным ситуациям, вопросам и проблемам. Этому процессу присуща открытость новым идеям.

1.     Критическое мышление–мышление самостоятельное

2.     Информация является отправным, а неконечным пунктом критического мышления.

3.     Критическое мышление начинается с постановки вопросов и уяснения проблем, которые нужно решить.

4.     Критическое мышление основано на убедительной аргументации.

5.     Критическое мышление–мышление социальное.

Данная технология позволяет решать такие задачи, как: образовательной мотивации, информационной грамотности, социальной компетентности.

Данная технология способствует не только усвоению конкретных знаний, а социализации ребенка, воспитанию доброжелательного отношения к людям. При обучении по данной технологии знания усваиваются значительно лучше, так как технология рассчитана не на запоминание, а на вдумчивый творческий процесс познания мира, на постановку проблемы, поиск ее решения.

Технология развития критического мышления включает в себя три стадии: вызова, осмысления и размышления.

Стадия вызова актуализирует имеющиеся знания учащихся, пробуждает интерес к теме. Именно здесь определяются цели изучения материала.

Стадия осмысления нового материала (новой информации, идеи, понятия). Здесь происходит основная содержательная работа ученика с текстом. Причем «текст» нужно понимать достаточно широко: это может быть чтение нового материала в учебнике, осмысление условия задачи, речь учителя…

Стадия размышления или рефлексии. Здесь ученик осмысляет изученный материал и формирует свое личное мнение, отношение к нему.

Все три стадии необходимо на уроке соблюдать, так как это отражает сложный мыслительный процесс. Эта особенность названной технологии существенно расширяет границы ее применимости.

Основные методические приемы развития критического мышления

1.                     Прием «Кластер»

2.                     Таблица

3.                     Учебно-мозговой штурм

4.                     Интеллектуальная разминка

5.                     Зигзаг, зигзаг-2

6.                     Прием «Инсерт»

7.                     Эссе

8.                     Приём «Корзина идей»

9.                     Приём «Составление синквейнов»

10.                 Метод контрольных вопросов

11.                 Приём«Знаю../Хочу узнать…/Узнал…»

12.                 Круги по воде

13.                 Ролевой проект

14.                 Да -нет

15.                 Приём «Чтение с остановками»

16.                 Приём « Взаимоопрос»

17.                 Приём «Перепутанные логические цепочки»

18.                 Приём «Перекрёстная дискуссия»

Рассмотрим приемы развития критического мышления на уроках математики:

Прием«Знаю–Хочу узнать - Узнал»(З-Х-У)

5-йкласс.Темаурока:«Сложение, вычитание обыкновенных дробей»

+ =

-=

*Как складывать дроби с разными знаменателями?

*Как вычитать дроби с разными знаменателями?

*Решение уравнений, задач, содержащих дроби с разными знаменателями

*Понятия: наименьший общий знаменатель, дополнительные множители.

*Чтобы сложить, вычесть дроби с разными знаменателями, нужно привести их к общему знаменателю.

*Алгоритм +,– дробей с разными знаменателями.

Данный прием предусматривает комплексный подход к изучению материала.

Учение начинается с активизации уже имеющихся знаний у учащихся. В первый столбец «Знаем» записываем идеи учеников, которые они предлагают.

Во второй столбик «Хотим узнать» предлагаем ученикам внести свои опорные мысли и идеи, которые у них возникли в процессе обсуждениятемы. Затем при чтении нового текста, учащиеся пытаются найти ответы на поставленные вопросы. Особым требованием при этом является – записать сведения, понятия и факты необходимо своими словами, не цитируя учебник. После изучения темы, учащиеся соотносят полученную информацию с той, которая была у них в начале урока.

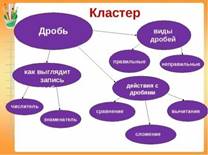
Прием«Кластер»

Данный прием–прием систематизации изучаемого материала в виде схемы. Прием «Кластер» я применяю как на стадии вызова, так и на стадии рефлексии, безусловно, он является способом мотивации к размышлению или до изучения нового материала, или формой систематизации изученной информации при подведении итогов.

Прием «Синквейн»

Это пятистрочная стихотворная форма, которая помогает описывать суть изучаемых понятий в лаконичной форме, а также осуществлять рефлексиюна основе полученных знаний.

Правило построения синквейна:

1   строка–одно существительное, выражающее главную тему cинквейна.

2   строка–два прилагательных, выражающих главную мысль.

3   строка–три глагола, описывающие действия в рамках  темы.

4   строка–фраза, несущая определенный смысл.

5     строка–заключение в форме существительного(ассоциацияспервым словом).

При составлении синквейна, у детей развивается не только критическое мышление, но и образное. Данная форма работы направлена на развитие у учащихся творческих способностей.

Пример синквейна:

1.Контрольная работа. 2.Интересная, понятная

3.   Пишем, строим, вычисляем.

4.   Тетрадь для контрольных работ.

5.   Математика.

1. Дроби.

2. Правильные, неправильные. 3.Решать,складывать,умножать.

4. Я умеюрешать основные задачи на дроби. 5.Легко.

Технология проблемного обучения

Проблемное обучение предполагает создание проблемных ситуаций под руководством учителя и активную самостоятельную деятельность учащихся по их разрешению.

Технологию проблемного обучения использую в основном на уроках: изучения нового материала и первичного закрепления.

Данная технология позволяет:

·         Активизировать познавательную деятельность учащихся на уроке, что позволяет справляться с большим объемом учебного материала;

·         Сформировать стойкую учебную мотивацию, а учение с увлечением– это яркий пример здоровьесбережения;

·         Использовать полученные навыки организации самостоятельной работы для получения новых знаний из разных источников информации;

·         Повысить самооценку учащихся, т.к. при решении проблемы выслушиваются и принимаются во внимание любые мнения.

Проблемная ситуация может создаваться, когда обнаруживается несоответствие имеющихся знаний и умений действительному положению вещей.

Второй вид проблемного изложения нового материала – проблемная ситуация создается, когда детям предлагается вопрос, требующий самостоятельного сопоставления ряда изученных фактов или явлений, и высказывания собственных суждений и выводов, или дается специальное задание для самостоятельного решения.

В общем виде структура проблемного урока выглядит следующим образом:

1)   Подготовительный этап;

2)   Этап создания проблемной ситуации;

3)   Осознание учащимися темы или отдельного вопроса темы в виде учебной проблемы;

4)   Выдвижение гипотезы, предположений, обоснование гипотезы;

5)   доказательство, решение и вывод посформулированной учебной проблеме;

6)   закрепление и обсуждение полученных данных, применение этих знаний в новых ситуациях

1.     Чтобы найти корень уравнения вида , нужно разделить на Если не делится нацело, то уравнение не имеет натуральных корней.Как объяснить тот факт, что уравнение имеет корень?

2.     Длина аквариума 80см, ширина 45см, а высота 55см. Сколько воды надо влить в этот аквариум, чтобы уровень воды был ниже верхнего края аквариума на 10 см?

Проблема: не знают понятие объема и формулу для нахождения объема параллелепипеда.

Учащиеся выбирают необходимую им информацию, используя текст учебника. Обсуждают решение задачи, делают вывод, записывают формулу в тетради.

Игровые технологии

Игра на ряду с трудом и ученьем – один и зосновных видов деятельности человека, удивительный феномен нашего существования.

По определению, игра- это вид деятельности в условиях ситуаций, направленных на воссоздание и усвоение общественного опыта, в котором складывается и совершенствуется самоуправление поведением. Игр существует очень много.

Какие задачи решает использование такой формы обучения:

·         Осуществляет более свободные, психологически раскрепощённый контроль знаний.

·         Исчезает болезненная реакция учащихся на не удачные ответы.

·         Подход к учащимся в обучении становится более деликатными дифференцированным.

Обучение в игре позволяет научить:

Распознавать, сравнивать, характеризовать, раскрывать понятия, обосновывать, применять

В результате применения методов игрового обучения достигаются следующие цели:

·         Стимулируется познавательная деятельность

·         Активизируется мыслительная деятельность

·         Самопроизвольно запоминаются сведения

·         Формируется ассоциативное запоминание

·         Усиливается мотивация к изучению предмета

Всё это говорит об эффективности обучения в процессе игры, которая является профессиональной деятельностью, имеющей черты, как учения, так и труда.

Пример1.«Прямоугольная система координат на плоскости» (6класс)

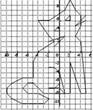
Игра «Соревнование художников»

На доске записаны координаты точек: КОШКА

(0;-4);(1;-8);(2;-8);(2;-2);(4;-8);(5;-8);(4;2);(3;3);(4;5);(4;7);(3;8);(2;10);

(1;8);(-2;6);(-4;6);(-2;3);(-1;2);(-4;0);(-5;-2);(-5;-5);(-7;-5);(-9;-6);(-10;-7); (-

10;-8);(-9;-9);(-7;-10);(-3;-10);(-2;-9);(-4;-8);(-6;-8);(-7;-7);(-6;-6);(-5;-6);(-

3;-8);(1;-8);(0;-7);(-2;-7);(-1;-7);(0;-6);(0;-4);(-1;-3);(-2;-3);Глаза:(-1;4);

(3;5);(5;6).

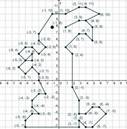
Отметить   на   координатной   плоскости   каждую   точку   и   соединить   с предыдущей отрезком. Результат – определенный рисунок.

Эту игру можно провести с обратным заданием: нарисовать самим любой рисунок, имеющий конфигурацию ломаной и записать координаты вершин.

Пример 2. Игра «Магические квадраты»

А) В клетки квадрата записать такие числа, чтобы сумма чисел по любой вертикали, горизонтали была равна 0.

Б) Записать в клетки квадрата числа -1;2;-3;-4;5;-6;-7;8;-9 так, чтобы произведение по любой диагонали, вертикали, горизонтали было равно положительному числу.

Пример 3. Игра  по теме «Сложение и вычитание целых чисел»

Задание: На земном шаре живут птицы – безошибочные «составители» прогноза погоды на лето. Название этих птиц зашифровано. Решив правильно примеры и сопоставив с соответствующей буквой вы узнаете название птицы.

Задание выполняют в парах, с последующей компьютерной проверкой.

а) 51 + (-20) + 35

б) -57 + 36 + (-63)

в) 42 + (-35) + (-32)

г) -39 + 11 + (-27)

д) 32 + (-73) + 98

е) – 45 -54 + 11

ж) 41 – 90 + 13

з) -13 -15 -28

Ф              М                А                  О                 Л               Г                И                 Н

66           -55             -25                -56             - 84          -3 6              57               -88      

Пример 4. Игра    «Дешифровка»

 Каждый член команды должен расшифровать слово, а затем отряд должен из этих слов составить высказывание великого полководца.

Каждый ученик получает лист с координатной плоскостью с  буквами русского алфавита – каждой букве соответствует своя точка плоскости;  также ученик получает зашифрованную записку.

Скачано с www.znanio.ru