Язык и алфавит. Кодирование. Позиционные и непозиционные системы счисления.

Урок 3-4, 10 класс – теория

Учитель: Брух Т.В.

Дата: ____________

Тема урока «Язык и алфавит. Кодирование. Позиционные и непозиционные системы счисления. Декодирование. Дискретность».

Цель: обобщить и применить для решения задач знания о способах перевода чисел; развитие познавательного интереса, творческой активности учащихся.

Задачи:

Обучающая:

- повторение и обобщение темы «системы счисления»

- стимулирование интереса к теме

Развивающая:

- развитие логического мышления, памяти, внимательности;

- развитие навыков индивидуальной практической деятельности.

Воспитывающая:

- формирование навыков самоорганизации и самоконтроля.

Ход урока.

1. Организационный момент. Учитель приветствует учащихся.

2. Проверка домашнего задания.

Проверка кодирования алфавита

Ответы на тест Информационные процессы

3. Изложение нового материала

Язык чисел, как и обычный язык, имеет свой алфавит. В том языке чисел, которым сейчас пользуются практически на всем земном шаре, алфавитом служат десять цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Это десятичная система счисления.

Система счисления – совокупность символов и правил их использования для представления чисел.

Существует два вида систем счисления:

Системы счисления

НЕПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ - это система счисления, в которой величина (значение) числа определяется как сумма или разность цифр в числе.

ПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ - это система счисления, в которой величина, обозначаемая цифрой, зависит от места (позиции) цифры в числе.

Например: рассмотрим три числа 156, 561 и 651.

Эти числа, разуется, различны, хотя в их записи участвуют одни и те же цифры. Различаются же записи расположением цифр – иными словами, тем, какую позицию занимает та или иная цифра.

Примером позиционной системы счисления является десятичная. Её алфавит: цифры от 0 до 9. Примеры записи чисел:

456=4*100+5*10+6=4*10²+5*10¹+6*10⁰

74,53=7*10+4*1+5*0,1+3*0,01=7*10¹+4*10⁰+5*10^-1+3*10^-2

Причины, по которой она оказалась общепринятой, совсем не математического характера. Десять пальцев рук - вот тот первоначальный аппарат для счета, которым человек пользовался с доисторических времен. По пальцам удобно считать от одного до десяти. Сосчитав до десяти, т.е. использовав до конца возможности нашего природного «счетного аппарата», естественно принять само число 10 за новую, более крупную единицу (единицу следующего разряда).

Древнее написание десятичных цифр: каждая цифра обозначает число по количеству углов в ней: 0 – нет углов, 1 – один угол, 2 – два угла и т.д.

Написание десятичных цифр претерпело существенные изменения. Формой, которой мы пользуемся, установилась в XVI веке.

Исторически десятичная система счисления сложилась и развивалась в Индии. В 13 веке индийская нумерация получает преобладание в Италии. В других странах Западной Европы она утверждается в 16 веке. Европейцы, заимствовавшие индийскую нумерацию от арабов, называли ее "арабской". Та форма, в которой мы их пишем, установилась в 16 веке. Это исторически неправильное название удерживается и поныне.

Однако десятичной системой счисления люди пользовались не всегда. В разные исторические периоды многие народы использовали другие системы счисления.

Простейшая и самая древняя – так называемая унарная система счисления. В ней для записи любых чисел (т.е. кодирования) используется один символ: палочка, узелок, зарубка, камушек

Даже у людей каменного века была необходимость что-либо считать, будь то количество оружия, или овец в стаде. Для того чтобы запомнить количество животных люди откладывали столько камней, сколько было овец. Тогда они могли выяснить, каков был приплод, или сколько овец погибло при наводнении.

Персидский царь Кир, начав войну со скифами, приказал своим союзникам охранять переправу через Дунай. А так как они не умели считать, Кир оставил их вождям связку из 60 веревок с узлами и приказал каждый день развязывать один узел. "Когда все узлы будут развязаны, - сказал он, -можете разрушить переправу и уходить домой".

До наших дней сохранилась римская система счисления. В римской системе счисления цифры обозначаются буквами латинского алфавита.

I

V

X

L

C

D

M

1

5

10

50

100

500

1000

Для записи промежуточных чисел используется правило: Меньшие знаки, поставленные справа от большего, прибавляются, а меньший знак, поставленный слева от большего, вычитается из него.

Пример: XXIV – 24, MCMXXXV – 1935.

В старину на Руси широко применялись системы счисления, отдаленно напоминающие римскую. С их помощью сборщики податей заполняли квитанции об уплате подати и делали записи в податной тетради.

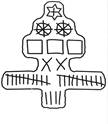
Например, 1232 р. 24 коп. изображается так:

звезда – 1000 р., колесо - 100 р., квадрат – 10 р., Х – 1 р., IIIIIIIIII – 10 к., I – 1 к. Дабы невозможно было сделать здесь никаких прибавлений, все таковые знаки очерчивать кругом прямыми линиями.

Славянская глаголическая нумерация была создана для переписки чисел в священных книгах западных славян. Использовалась она нечасто, но достаточно долго. Использовалась она с VIII по XIII в.

Славянская кириллическая алфавитная нумерация была создана вместе со славянской алфавитной системой для перевода священных библейских книг для славян греческими монахами братьями Кириллом и Мефодием в IX веке. Эта форма записи чисел получила большое распространение в связи с тем, что имела полное сходство с греческой записью чисел. До XVII века эта форма записи чисел была официальной на территории современной России, Белоруссии, Украины, Болгарии, Венгрии, Сербии и Хорватии. До сих пор православные церковные книги используют эту нумерацию.

 В древнейшее время в Греции была распространена так называемая Аттическая нумерация. В этой нумерации числа 1, 2, 3, 4 изображались соответствующим количеством вертикальных полосок. Число 5 записывалось знаком (древнее начертание буквы "Пи", с которой начиналось слово "пять" - "пенте". Числа 6, 7, 8, 9 обозначались сочетаниями этих знаков: .

Число 10 обозначалось - заглавной "Дельта" от слова "дека" - "десять". Числа 100, 1 000 и 10 000 обозначались H, X, M. Числа 50, 500, 5 000 обозначались комбинациями чисел 5 и 10, 5 и 100, 5 и 1 000.

Примерно в третьем веке до нашей эры аттическая нумерация в Греции была вытеснена другой, так называемой "Ионийской" системой. В ней числа 1 - 9 обозначаются первыми буквами греческого алфавита, над которыми ставились черточки.

Система счета древних египтян насчитывает семь знаков, передающих разряды чисел. Запись цифр внутри каждого из разрядов производилась простым увеличением количества знаков по принципу простейшего сложения.

Например, число "1" передавалось одной чертой (I), "2"- , соответственно,- двумя (II), "3" - тремя (III)...."8" - восемью (IIIIIIII), "9" - девятью (IIIIIIIII) и т.д.

Числа, содержащие несколько разрядов единиц, записывались по такому же принципу; при этом единицы высших разрядов выносились в начало записи.

Для обозначения чисел высших разрядов египтяне использовали запись умножения.

Довольно широкое распространение имела двенадцатеричная система счисления. Вместо, того чтобы сказать «двенадцать», мы иногда говорим «дюжина». Происхождение ее тоже связано со счетом на пальцах. Считали фаланги пальцев на руке кроме большого. 4 пальца по три фаланги всего 12. Элементы двенадцатеричной системы счисления сохранились в Англии в системе мер (1 фут = 12 дюймов) и в денежной системе (1 шиллинг = 12 пенсам). Где вы еще встречали счет по 12? (Нередко и мы сталкиваемся с этой системой в быту: чайные и столовые сервизы на 12 персон, в году 12 месяцев, на циферблате 12 часов, а яйца продают по 12 штук за границей).

Пятеричная система счисления по свидетельству известного исследователя Африки Стэнли у ряда африканских племен была распространена. Долгое время пятеричной системой счисления пользовались и в Китае. Некоторые племена на филип­пинских островах используют ее и в наши дни, а в цивилизованных странах ее реликт сохранился в виде школьной пятибалльной шкалы оценок. Очевидна связь этой системы со строением человеческой руки.

В сказке "Конёк-Горбунок", написанной П. П. Ершовым, есть примечательный эпизод. Царь, увидев златогривых коней и пожелав их заполучить, вступает с Иваном в торг.

Ну, я пару покупаю.

Продаешь, ты? — Нет, меняю.

Что в промен берешь добра? —

Два — пять шапок серебра. —

То есть это будет десять.

Царь тотчас велел отвесить...

Иван, не будучи большим грамотеем, торгуясь с царем, оперирует пятками, а более продвинутый в арифметике монарх переводит его примитивный счет в десятеричную систему.

Двадцатеричная система счисления была принята у ацтеков и майя – народов, населявших в течение многих столетий обширные области Американского континента и создавшие там высочайшую культуру, в том числе и математическую. Также 20-ричная система счисления была принята у кельтов, населявших Западную Европу, начиная со второго тысячелетия до н.э.. Основу для счета в этой системе счисления составляли пальцы рук и ног. Некоторые следы 20-ричной системы счисления кельтов сохранились во французской денежной системе. Основная денежная единица – франк делится на 20 (1 франк = 20 су).

Шестидесятеричная система счисления или так называемая «вавилонская» весьма сложная система, существовавшая в Древнем Вавилоне.

Мнения историков по поводу того, как именно возникла эта система счисления, расходятся. Существуют две гипотезы: 1) слияние двух племен, одно из которых пользовалось шестеричной, а другое десятичной. Т.е. она возникла в результате политического компромисса. 2) древние вавилоняне считали продолжительность года равной 360 суткам, что естественно связано с числом 60.

Отголосками использования этой системы счисления дошли до наших дней 1 час = 60 мин., 1⁰ = 60’. В целом 60-ричная система счисления громоздка и неудобна.

4. Этап закрепления изученного.

Работа с моделью "Переход из одной системы счисления в другую" 

Перевод чисел из одной системы счисления в другую – строго говоря, тема следующего урока. Однако особенно для сильной группы учащихся можно анонсировать тему путем постановки проблемного вопроса. Как развернутая форма записи числа в двоичной системе счисления может быть использована для перевода чисел из двоичной в десятичную систему счисления? Учащиеся работают с моделью на локальных компьютерах или учитель вызывает учащегося, модель проецируется на экран или интерактивную доску, организуется демонстрационная работа модели, высказываются гипотезы, проверяются, формулируется правило, которое учащиеся заносят в тетради.

Вторая форма работы – разбор принципов работы с моделью, вынесение в домашнее задание изучение правила перевода чисел из одной системы счисления в другую.

Третья формы работы – проведение блиц-тестирования, устного сета проверка результатов с помощью модели.

5. Практическая часть

Запишите в тетради:

·        Представьте числа в позиционной системе счисления и переведите в двоичную систему счисления: IV, XIX, MCIVI.

·        Запишите год, месяц и число своего рождения с помощью римских цифр.

·        Запишите в развернутом виде число: А₁₀ = 54334 А₁₀ = 23122  в двоичную систему счисления.

·        ЗАПИШИТЕ РИМСКОЕ ЧИСЛО В ДЕСЯТИЧНОЙ СИСТЕМЕ СЧИСЛЕНИЯ:

MCMLXXXIV=

·        ЗАПИШИТЕ СЛЕДУЮЩИЕ ЧИСЛА В ВИДЕ:

423₁₀=

10111,101₁₀=

6. Подведение итогов.

7. Домашнее задание Теоретический материал