Y=ctgx ֆունկցիայի հատկություններն ու գրաֆիկը

y=ctgx ֆունկցիայի հատկություններն ու գրաֆիկը

   y=ctgx ֆունկցիան որոշված է x≠πn,n∈Z արգումենտների համար, կենտ է և պարբերական՝  π պարբերությամբ:

   Ուստի, ֆունկցիայի գրաֆիկը բավական է կառուցել (0;π) բազմության վրա, ապա պարբերաբար շարունակել դեպի ձախ և աջ:

   y=ctgx ֆունկցիայի գրաֆիկը, երբ արգումենտը պատկանում է (0;π) միջակայքին,  անվանում են կոտանգենսի գլխավոր գիծ:

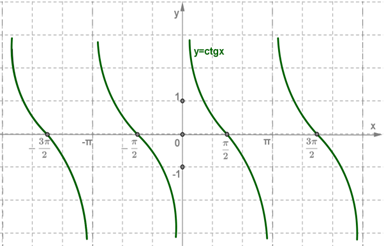
    y=ctgx ֆունկցիայի հատկությունները

 1. y=ctgx ֆունկցիան որոշված է x≠πn,n∈Z թվերի համար:

 2. y=ctgx ֆունկցիայի արժեքների բազմությունը ամբողջ թվային առանցքն է՝ E(ctgx)=R:

 3. y=ctgx-ը π-պարբերական ֆունկցիա է:

 4. y=ctgx-ը կետը ֆունկցիա է:  

 5. ctgx=0, եթե x=π/2+πn, n∈Z:

 6. y=ctgx ֆունկցիայի արժեքները դրական են (πn;π/2+πn),n∈Z միջակայքերում և բացասական են (π/2+πn;π+πn),n∈Z. միջակայքերում:

 7. y=ctgx ֆունկցիան նվազում է (πn;π+πn),n∈Z. միջակայքերում:

 8. y=ctgx ֆունկցիան էքստրեմումի կետեր չունի: