За страницами учебника математики. Способы умножения чисел.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1. Таблица умножения на 9

 

2. Таблица умножения на пальчиках (умножение на 9)

Положить все 10 пальцев веером перед собой ладошками вниз и загадать число, которое хочешь умножить на 9. Например, 6. Найти 6-й по счету палец (считать от левого мизинца до правого): слева от этого [т.е. шестого] пальца будут пять пальцев, это - число десятков, справа от него будут 4

пальца - это единицы. Итак: 9х6 = 54.

 

 

3. Умножение на 6, 7 и 8

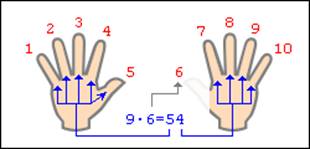
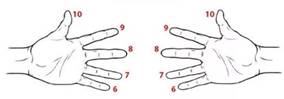
Поверните кисти ладонями к себе и присвойте каждому пальцу цифры от 6 и до 10 начиная с мизинца.

Теперь попробуем умножить, например, 7х8. Для этого соедините палец №7 на левой руке с пальцем №8 на правой.

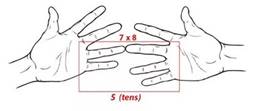
А теперь считаем пальцы: количество пальцев под соединенными — это десятки.

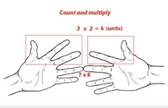
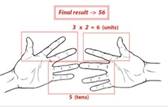
А пальцы левой руки, оставшиеся сверху, умножаем на пальцы правой — это и будут наши единицы (3х2=6). Десятки и единицы складываем, получаем число 56.

4. Крестьянский способ

Суть заключается в том, что умножение любых чисел сводится к ряду последовательных делений одного числа пополам, при одновременном удвоении другого числа. Например, 32∙13

 

32∙13=416. Последнее число в правой таблице есть искомый результат.

 

Если в каком то шаге в делении возникает остаток, то он отбрасывается. И в этом случае вычеркиваются те строчки, где в обеих частях таблицы стоят четные числа. Складывают оставшиеся числа в правом столбце. Это и есть искомое произведение. Например, 13∙11

 

 

 13∙11=11+44+88=143

 

 

 

 

 

 

 

 

 

5. Итальянский способ умножения «Сеткой»

Например, умножим 6827 на 345.

1) Вычерчиваем квадратную сетку и пишем одно из чисел над колонками, а второе по высоте.

 

2)Умножаем число каждого ряда последовательно на числа каждой колонки.

 

3) Заполняем всю сетку и складываем числа, следуя диагональным полосам. Начинаем складывать справа налево снизу. Если сумма одной диагонали содержит десятки, то прибавляем их к единицам следующей диагонали.

Ответ: 2355315.

 

 

 

 

 

 

 

6. Палочки Непера

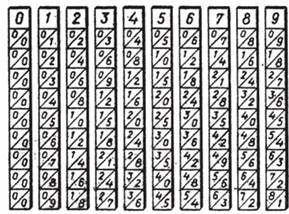
Джон Непер, шотландский математик XVI века – изобретатель счетного прибора, в дальнейшем получившего название «палочки Непера».

	Умножим числа 2191 и 272 с помощью палочек Непера. Палочки, соответствующие значениям каждого разряда множимого, выкладываются в ряд так, чтобы цифры сверху каждой палочки составляли множимое. Слева прикладывается палочка – указатель строк, по которой выбирают  строки,  соответствующие  разрядам множителя. Суммируем цифры по наклонным полоскам справа налево, при необходимости перенося «в уме» в
соседнюю слева полоску единицу или другое число. Результат умножения 2191 на 2 – это 4 382. Находим результат умножения 2 191 на 7. Получаем 15 337 Складываем все полученные результаты, учитывая порядок разряда: 2191 ∙ 272=595952    4382 + 15337        4382    595952

7. Графический способ (Японский метод)

Суть метода: многозначное число изображается с помощью линий, причем различные разряды этого числа имеют разный цвет. Затем считают точки пересечения линий, складывают по разрядам.

Например, 64 · 53.

Число 64 это 6 десятков и 4 единицы. Изобразим горизонтально 6 линий красного цвета и четыре синих. Число 53 это 5 десятков и 3 единицы, изобразим вертикально 5 линий красного и 3 синего цвета.

 

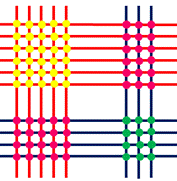
Всего у нас получилось 3 группы пересечения – пересечение красных линий; красных и синих линий; синих линий. Значит, результат умножения будет числом, который состоит из 3 разрядов – сотен, десятков и единиц.

Количество пересечения красных линий – 30 (30 сотен, то есть 3000), синие и красные пересекаются в 38 точках (38 десятков, то есть 380). Количество точек пересечения синих линий равно 12 (12 единиц). В ответе получаем 3000+380+12=3392.

 

 

 

 

 

 

8. Умножение числа на 9.

Чтобы умножить число на 9, нужно к нему приписать 0 и отнять исходное число.

Например: 72 · 9 = 720 – 72 = 648.

 

9. Умножение двухзначных чисел на 11.

Чтобы умножить число на 11 надо мысленно раздвинуть цифры этого числа, поставить между ними сумму этих цифр.

45 ∙ 11 = 495

53 ∙ 11 = 583

«Краешки сложи, в серединку положи» - эти слова помогут легко запомнить данный способ умножения на 11.

Чтобы умножить на 11 число, сумма цифр которого 10 или больше 10, надо мысленно раздвинуть цифры этого числа, поставить между ними сумму этих цифр, а затем к первой цифре прибавить 1, а вторую и третью цифру оставить без изменения.

87 ∙ 11 = 957

94 ∙ 11 = 1024

Такой способ подходит только для умножения двузначных чисел

 

10. Умножение на 37

Прежде чем научиться устно умножать на 37,надо хорошо знать признак делимости и таблицу умножения на 3. Чтобы устно умножить число на 37, надо это число  разделить на 3 и умножить на 111.

Примеры:

24 · 37 = (24 : 3) · 37 · 3 = 8 · 111 = 888;  

18· 37 = (18 : 3) · 111 = 6 · 111 = 666.

11. Умножение двухзначных чисел на 111, 1111 и т. д., зная правила умножения двузначного числа на число 11.

Если сумма цифр первого множителя меньше 10, надо мысленно раздвинуть цифры этого числа на 2, 3 и т.д. шага, сложить данные цифры и записать их сумму между раздвинутыми цифрами соответствующее количество раз. Заметьте, количество шагов всегда меньше количества единиц на 1.

Пример:

24 · 111=2 (2+4) (2+4) 4 = 2664 (количество шагов - 2)

24 · 1111=2 (2+4) (2+4) (2+4) 4 = 26664 (количество шагов - 3)

42 · 111 111 = 4 (4+2) (4+2) (4+2) (4+2) (4+2) 2 = 4666662. (количество шагов – 5)

Если единиц 6, то шагов будет 1 меньше, то есть 5.

Если единиц 7, то шагов будет 6 и т.д.

Немного сложнее выполнить устное умножение, если сумма цифр первого множителя равна 10 или более 10.

Примеры:

86 · 111 = 8 (8+6) (8+6) 6 = 8 (14) (14) 6 = (8+1) (4+1) 46 = 9546.

В этом случае надо к первой цифре 8 прибавить 1, получим 9, далее 4+1 = 5; а последние цифры 4 и 6 оставляем без изменения. Получаем ответ 9546.

 

12. Умножение числа на 1,5.

Чтобы умножить число на 1,5, нужно к исходному числу прибавить его половину.

Например:

34 · 1,5 = 34 + 17 = 51;

146 · 1,5 = 146 + 73 = 219

 

13. Умножение двузначного числа на 101, 1001 и т.д..

Пожалуй, самое простое правило: припишите ваше число к самому себе. Умножение закончено. Пример:

32 · 101 = 3232;                 

47 · 101 = 4747;

324 · 1001 = 324 324;      

675 · 1001 = 675 675; 

6478 · 10001 = 64786478;

846932 · 1000001 =  846932846932.

 

14. Умножение на 5; 25; 125.

Сначала умножить на 10, 100, 1000 и результат разделить на 2, 4, 8

32 · 5 = 32 · 10: 2 = 320: 2 = 160

84· 25 = 84 · 100: 4 = 8400: 4 = 2100

24 ·125 = 24 · 1000: 8 = 24000: 8 = 3000

Можно иначе: 32 · 5 = 32: 2 ·10 = 160

 

15. Умножение на 22, 33, … , 99

Чтобы двузначное число умножить на 22,33,…, 99, надо этот множитель представить в виде произведения однозначного числа (от 2 до 9) на 11, то есть 33 = 3 х 11; 44 =  4 х 11 и т.д. Затем произведение первых чисел умножить на 11.

  Примеры:

  18 · 44 = 18 · 4 · 11 = 72 · 11 = 792;

  42 · 22 = 42 · 2 · 11 = 84 · 11 = 924;

  13 · 55 = 13 · 5 · 11 = 65 · 11 = 715; 

  24 · 99 = 24 · 9 · 11 = 216 · 11 = 2376.

 

 

.

 

16. Возведение в квадрат двузначного числа, оканчивающегося на 5.

Чтобы возвести в квадрат двузначное число, оканчивающееся на 5, нужно цифру десятков умножить на цифру, большую на единицу, и к полученному произведению приписать справа число 25.

25 · 25 = 625

2 · (2 + 1) = 2 · 3 = 6, пишем 6; 5 · 5 = 25, записываем 25.

35 · 35 = 1225

3 · (3 + 1) = 3 · 4 = 12, пишем 12; 5 · 5 = 25, записываем 25.

 

17. Возведение в квадрат двузначного числа, начинающегося на 5.

Для возведения в квадрат двузначного числа, начинающегося на пять, нужно прибавить к 25 вторую цифру числа и приписать справа квадрат второй цифры, причем если квадрат второй цифры – однозначное число, то перед ним надо приписать цифру 0.

Например:
52² = 2704, т.к. 25 +2 = 27 и 2² = 04;
58² = 3364, т.к. 25 + 8 = 33 и 8² = 64.