Зачетная работа по теме «Квадратные корни»

Зачетная работа по теме «Квадратные корни» - ПРИМЕНЕНИЕ СВОЙСТВ АРИФМЕТИЧЕСКОГО КВАДРАТНОГО КОРНЯ - КВАДРАТНЫЕ КОРНИ

Цель: проверка знаний учащихся по вариантам одинаковой сложности.

Ход урока

I. Сообщение темы и цели урока

II. Характеристика зачетной работы

По сравнению с контрольной работой в зачетной увеличено количество заданий. Соответственно, у учащихся возрастает возможность выбора задач. Все задания разбиты на три блока: А, В и С. Самые простые задачи находятся в части А, более сложные — в части В, еще сложнее — в части С. Каждая задача из А оценивается в 1 балл, из В — в 2 балла, из С — в 3 балла. Поэтому за правильное решение всех задач блока А можно получить 7 баллов, блока В — 8 баллов и блока С — 9 баллов (всего 24 балла). Оценка «3» ставится за 6 баллов, оценка «4» — за 10 баллов, оценка «5» — за 14 баллов.

Так как эта работа является зачетной, то в нее не включены принципиально новые задачи. Поэтому разбор заданий работы можно и не проводить (решения задач могут быть вывешены на стенде). Для стендового размещения разбор заданий приводится.

III. Задания зачетной работы

А

1. Вычислите: 

2. Сравните числа 

3. Найдите значение выражения 

4. Сократите дробь 

5. Решите уравнение 

6. Упростите выражение 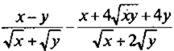 и найдите его значение при 

7. Постройте график функции 

В

8. Известно, что Найдите значение выражения 

9. Упростите выражение 

10. Сравните числа 

11. Решите уравнение 

С

12. Сократите дробь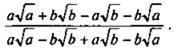 

13. Упростите выражение 

Ads by optAd360

14. Постройте график зависимости y(x), если выполнено условие 

IV. Разбор заданий зачетной работы

1. В скобках вынесем множители из-под знаков корня и приведем подобные члены. Получаем: 

Ответ: 4.

2. В первом числе внесем множитель под знак корня:  Так как 63 > 62, то  т. е. 

Ответ: 

3. Учтем теорему о произведении корней и формулу разности квадратов. Получим: 

Ответ: 7.

4. Разложим числитель и знаменатель дроби на множители и сократим дробь: 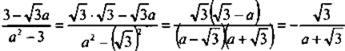 (при а ≠ ±√3).

Ответ: 

5. Учтем свойства квадратного корня и получим уравнение:  или  или |х - 3| = 2. Тогда величина x - 3 = ±2, откуда х1 = 5 и х2 = 1.

Ответ: х1 = 5, х2 = 1.

6. Разложим числители и знаменатели дробей на множители и сократим дроби. Получаем:

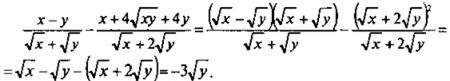
Теперь подставим данное значение y = 1/81 и найдем: 

Ответ: 

7. Область определения функции

 задается условиями: х ≥ 0 и -х ≥ 0 (подкоренные выражения неотрицательны). Эта система неравенств имеет единственное решение х = 0. Тогда и у = 0. Поэтому графиком данной функции является единственная точка (0; 0) — начало координат.

Ответ: начало координат.

8. По свойству арифметического квадратного корня  Теперь подставим данные значения  и получим:  Учтено, что  и 

Ответ: 2.

9. В скобках приведем дроби к общему знаменателю и вычтем их. Имеем: 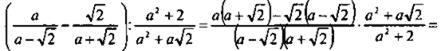 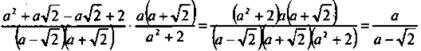(при а ≠ 0; ±√2).

Ответ: 

10. В числе Л сложим дроби и получим:  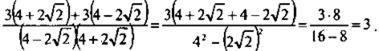Так как  то А > В.

Ответ: А > В.

11. Обе части уравнения  возведем в квадрат  Выразим  Еще раз возведем обе части этого уравнения в квадрат: 2 – х = 169, откуда x = -167.

Ответ: x = -167.

12. Сгруппируем члены в числителе и знаменателе, разложим их на множители и сократим дробь. Получаем: 

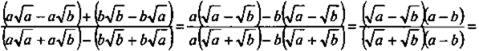
Ответ: 

13. Прежде всего надо заметить, что подкоренные выражения являются полными квадратами:  и  После этого легко упростить данное выражение:

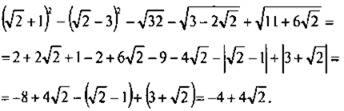
Ответ: 

14. Так как левая часть равенства  по определению арифметического квадратного корня неотрицательна, то и правая часть должна быть неотрицательной, т. е. 1 - у ≥ 0, откуда у ≤ 1. Возведем в квадрат обе части данного равенства: у2 - 2х2 + 1 = (1 – y)2 (при этом подкоренное выражение у2 - 2х2 + 1 неотрицательно, т. к. оно равно (1 - у)2 ≥ 0) или у2 - 2х2 + 1 = 1 - 2у + у2, или у = х2 (причем у ≤ 1). Поэтому построим параболу у = х2 и выберем ту ее часть, для которой у ≤ 1 (сплошная линия).

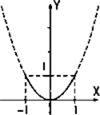
Ответ: см. график.

Скачано с www.znanio.ru