
Задачи характеризации
Целью характеризации, т.е. математического описания объекта управления является установление форм связи между параметрами процесса. Уравнения связи, в которых отражаются физические законы, определяющие протекание процесса в данном объекте управления, могут быть записаны в различных формах. Форма характеризации процесса должна быть адекватной в смысле требований, предъявляемых к ней. Такими требованиями могут быть:
· наглядность или простота физического смысла связей между переменными (при теоретическом анализе);
· простота нахождения параметров связей (при идентификации);
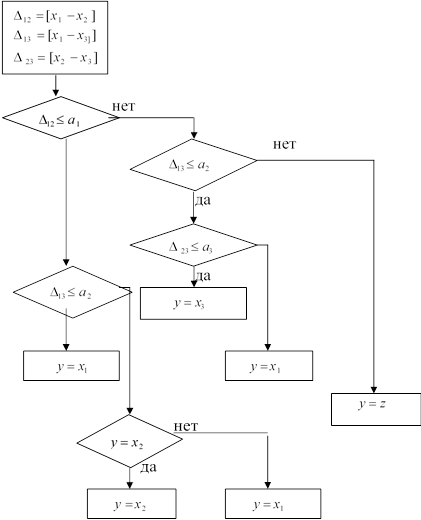
Рис. 9.2 Блок-схема алгоритма контроля достоверности информации
· простота синтеза оптимального управления;
· простота анализа ТОУ при решении конкретных задач анализа качества систем управления, устойчивости и др.
![]() Поскольку всем
требованиям одновременно удовлетворять трудно, то на разных этапах синтеза
программного обеспечения ТП можно использовать различные формы характеризации,
которые связаны между собой и при необходимости могут переходить от одних форм
к другим, более удобным на данном этапе для решения поставленных задач,
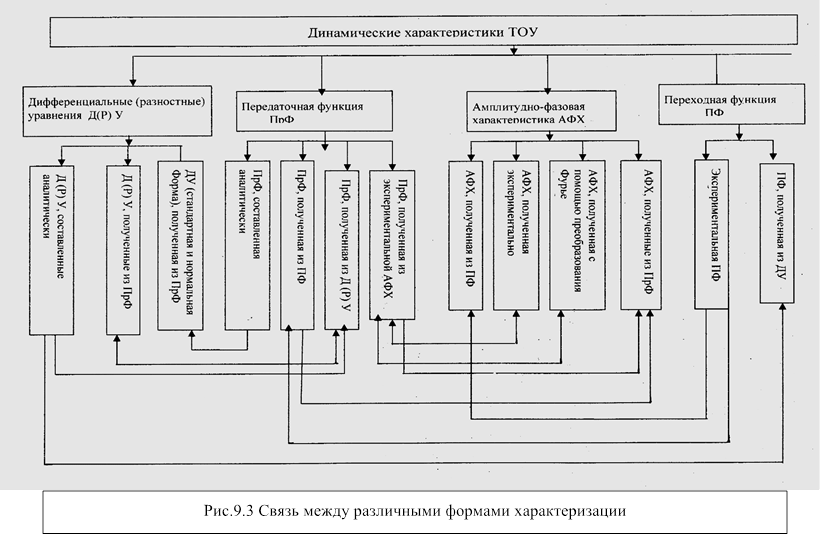
используя алгоритмы перехода. Структурная схема связей между различными формами
характеризации изображена на (рис.9.3.).
Поскольку всем
требованиям одновременно удовлетворять трудно, то на разных этапах синтеза
программного обеспечения ТП можно использовать различные формы характеризации,
которые связаны между собой и при необходимости могут переходить от одних форм
к другим, более удобным на данном этапе для решения поставленных задач,
используя алгоритмы перехода. Структурная схема связей между различными формами
характеризации изображена на (рис.9.3.).
Так как реальные процессы являются многомерными, нестационарными, с голономными связями, с распределенными
параметрами, то необходимо применять приемы упрощения математических моделей, к которым относятся:
· расчленение многомерной системы на ряд систем меньшей размерности;
· понижение размерности модели за счет оставления в ней наиболее существенных воздействий и учета прочих в параметрической форме;
· принятие гипотезы стационарности или кваистационарности модели;
· линеаризация нелинейных связей в модели управления в некоторой области изменения переменных;
· пренебрежение динамическими свойствами объекта управления.
Перечисленные допущения позволяют описывать динамические свойства объекта обыкновенными линейными дифференциальными уравнениями с постоянными коэффициентами.
Использование ЦВМ для управления процессом приводит к тому, что на вход объекта подается управляющий сигнал, квантованный по времени. Выходной сигнал также рассматривается только в дискретные моменты времени. В этом случае для характеризации процесса можно применять соответствующую ему дискретную модель в виде линейных разностных уравнений с постоянными коэффициентами и др.
На практике применяют два способа характеризации объектов управления:
· с помощью характеристик ˝вход выход˝;
· с помощью уравнений для переменных состояния.
Описание объекта первым способом является субъективным и неполным. Оно отражает динамические свойства только агрегированных моделей каналов прохождения управляющих и возмущающих воздействий. Другой подход связан с описанием поведения объекта управления в абстрактном пространстве состояний. Этот путь оказывается более плодотворным, так как описание в терминах пространства состояний более объективно и полно, чем описание характеристиками ˝вход выход˝, которые определяют лишь одну часть объекта, а именно, полностью управляемую и наблюдаемую часть.
 |
|||
В АСУ ТП более эффективными, с вычислительной точки зрения, являются алгебраические методы линеаризации в виде матрично-векторных уравнений состояния, записанных в рекуррентной форме:
Xk=Fk (X k -i ,V k -i ,Zk-j);
Xn=X-[K´ ∆t;] – состояние объекта управления в дискретный момент времени;
∆t — интервал дискретизации;
Vk-i — управление объектом в момент (k-i)´ ∆t (величина i≥1 характеризует возможное запаздывание по каналу управления);
Z k - j , — возмущение в момент (к - i)´ ∆t (величина j≥1 характеризует возможное запаздывание по каналу возмущения);
Fk — вектор-функция связей между переменными.
Вычисляемые ЭВМ значения управляющих воздействий должны быть найдены как функции от состояния (настоящего и прошлого) и возмущений (настоящих и будущих):
V k = φ k (X k ,……, X k - p , Z k ,……., Z k + S) φ k - вектор функция, p ≥ 0, s ≥ 0
Вопросы для самопроверки:
1. Назначение алгоритмов контроля.
2. Особенности в лесном комплексе.
3. АСУТП как система функциональных задач.
4. Что такое градуировка и коррекция показаний датчиков?
5. Назвать и показать случаи фильтрации и сглаживания.
6. Для чего применяют интерполяцию и экстраполяцию?
7. Назвать и показать методы определения функций распределения.
8. Методы определения математического ожидания.
9. Методы определения функций корреляции. 10.Методы определения спектральной плотности.
11. Назначение алгоритмов контроля достоверности исходной информации и методы их определения.
12. Назначение и методы определения задач характеризации.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.