Задачи на применение производной в математике.

Задачи на применение производной в математике.

Задача 1.  Площадь круга вычисляется по формуле S =… .

Докажите, что длина окружности С является производной от площади круга того же радиуса.

Задача 2. Задача Дидоны.

Дидона – дочь тирского царя, основательница и царица Карфагена. Высадившись на побережье Тунисского залива она основала карфагенский кремль Бирсу, купив у местного вождя участок земли.

Легенда гласит, что местные жители согласились продать ей столько земли, сколько можно огородить одной бычьей шкурой. Дидона разрезала бычью шкуру на тонкие ремешки, связала их и получила веревку, длиной 2000 м, огородила этой веревкой прямоугольный участок, примыкающий к побережью.

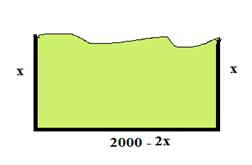
Вопрос: Какую наибольшую площадь земли могла купить Дидона?

План решения.

1.    Составить выражение для вычисления площади S изображенной фигуры, считая ее прямоугольником.

2.    Найти производную Sʹ (х).

3.    Приравнять производную к нулю  Sʹ (х) = 0

4.    Найти стороны прямоугольника.

5.    Вычислить его площадь в м²   и км².

Задача 3. При движении тела по прямой его координата меняется по закону X(t) =  -  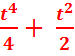+t (м), где t- время движения в секундах. Найти через сколько секунд ускорение будет равно 5   ?

Задача  4.  Угол поворота тела вокруг оси изменяется в зависимости от времени t по закону φ(t) = 0,1 t² – 0,5 t + 0,2  рад.

Найти, в какой момент времени угловая скорость была равна 3,5   .

Задача 5. Тело, массой m =5 кг, движется прямолинейно по закону S(t) = 1 –t +t² (метров), t –время в секундах. Найти кинетическую энергию тела E =  через 10 секунд после начала движения.

Задача 6. Найти угол  в градусах между касательной к графику функции   y =   в точке с абсциссой х₀ = 3 и осью Ох.

Задача 7. Найти угол  в градусах между касательной к графику функции   y = +   точке с абсциссой х₀ = 0 и осью Оу.

Задача 8. Найти точки и написать уравнения касательных к кривым f(x) = x³ – x -1  и g(x) = 3x² - 4x +1 , если эти касательные параллельны.

Задача 9. Найти угловой коэффициент наклона касательной к графику функции f(x) = cos 4x ˔ sin 4x  в точке х₀ = - .

Задача 10. Прямая касается гиперболы у =    в точке (1 ; 4). Найти площадь треугольника, ограниченного этой касательной и осями координат.

Задача 11. Найти промежутки возрастания и убывания функции  у = 1 +  .

Задача 12. Найти промежутки возрастания и убывания функции  у = 3 ^{х2 -х.}

Задача 13. Найти точки экстремума и значение функции в них для функции  f(x) = sin x +  sin 2x    \

Задача 14. Построить график функции y = x˔ e^x  

 Задача 15.   Из всех прямоугольников с периметром, равным

24 см, найти прямоугольник наибольшей площади. Вычислить его площадь.

 Задача 16.  Найти наименьшее значение функции  f(x) = ln x – x на отрезке [  ; 3].

Ответы на задачи.

1.    C = 2πR;  S = πR²   Sʹ =2πR     C = Sʹ.

2.    Стороны 500м и 1000м., площадь 500000 кв.м = 0,5кв.км.

3.    2 сек.

4.   20 сек.

5.   902,5 Дж.

6.   - 60° .

7.    45° .

8.    (1; -1)   у =2х – 3;   (1;0)  у= 2х -2 .

9.  угловой коэффициент   равен 2.

10.  8 кв.ед.

11. Убывает на промежутках ( - ; 0) и (4; +).

12.  Возрастает на промежутке ( ; +) ; убывает на промежутке ( - ; ).

13. X_max =  + 2πn, nZ , y _max =  ; X_min= -  + 2πn, nZ , y_min = -  

14.     Для графика:  X_min= -1    y_min   - 0,37.  На ( - ; -1) –функция убывает; на  (-1; +) – возрастает.

15.  Квадрат со стороной  6 см.    S = 36 см²

16.   1.