Задачи: определение, структура, классификация на уроках математики в начальной школе

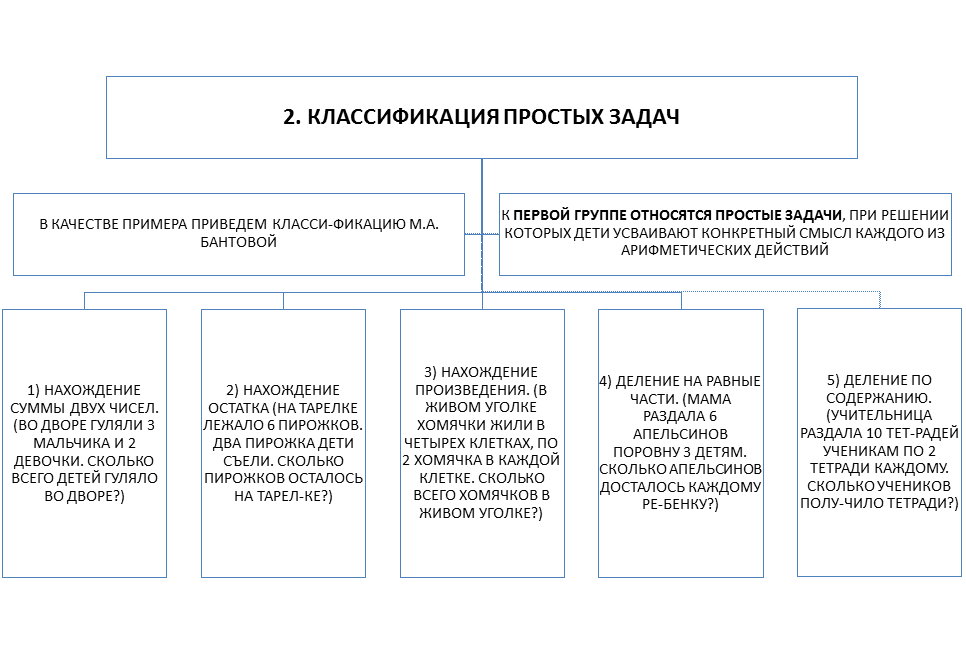
К третьей группе относятся задачи, при решении которых раскрываются понятия разности и кратного отношения. К ним относятся простые задачи, связанные с понятием разности

3. ЭТАПЫ ОБУЧЕНИЯ РЕШЕНИЮ ПРОСТЫХ ЗАДАЧ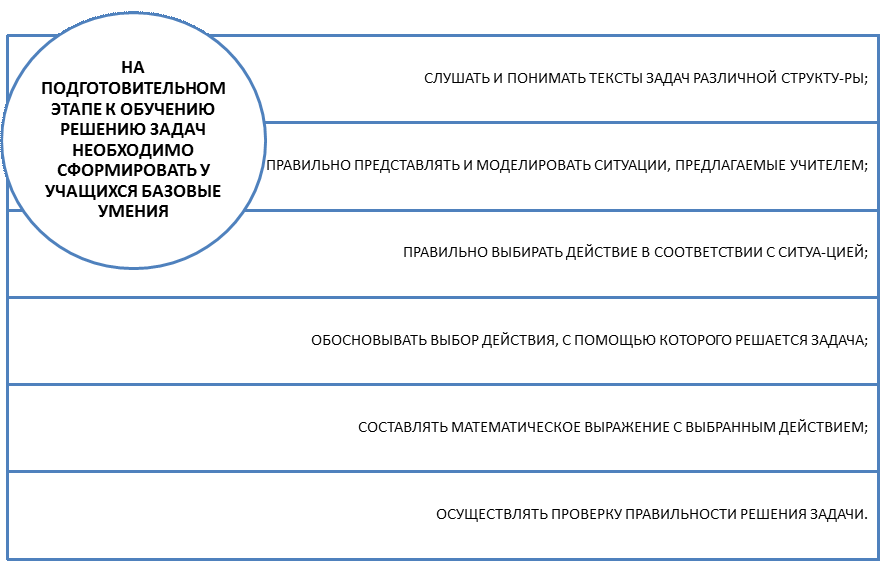

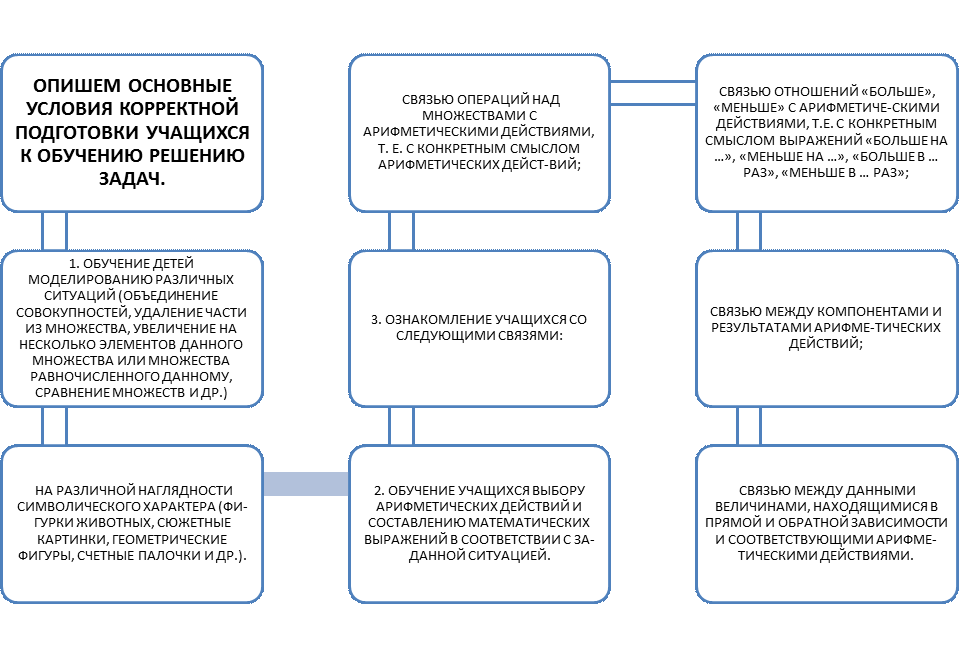
ПРОЦЕСС РЕШЕНИЯ ЗАДАЧИ

Словесная модель Графическая     Символическая модель

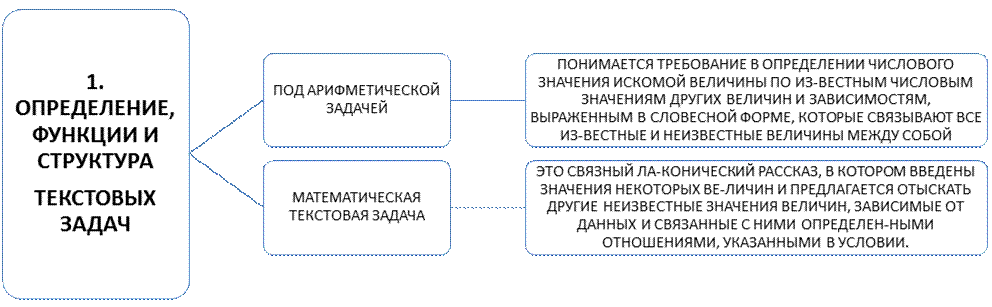
1.3. МЕТОДЫ РЕШЕНИЯ ТЕКСТОВЫХ  МАТЕМАТИЧЕСКИХ ЗАДАЧ

1. ВИДЫ МЕТОДОВ РЕШЕНИЯ ТЕКСТОВЫХ ЗАДАЧ

В КУРСЕ МАТЕМАТИКИ НАЧАЛЬНЫХ КЛАССОВ ИСПОЛЬЗУЮТ :

−     Практический,

−     Арифметический,

−     Алгебраический и

−       Геометрический,

В ЧАСТНОСТИ, ГРАФИЧЕСКИЙ МЕТОДЫ РЕШЕНИЯ ЗАДАЧ. ОСНОВНЫМИ МЕтОДАМИ РЕШЕНИЯ ТЕКСТОВЫХ ЗАДАЧ ЯВЛЯЮТСЯ АРИФМЕТИЧЕСКИЙ И АЛГЕБРАИЧЕСКИЙ МЕТОД.

2. ХАРАКТЕРИСТИКА АРИФМЕТИЧЕСКОГО МЕТОДА РЕШЕНИЯ ЗАДАЧ,

СУЩНОСТЬ АРИФМЕТИЧЕСКОГО МЕТОДА РЕШЕНИЯ СОСТОИТ В ПОСЛЕДОВАТЕЛЬНОМ ВЫПОЛНЕНИИ СЛЕДУЮЩИХ ДЕЙСТВИЙ:

−          РАСЧЛЕНЕНИЕ СОСТАВНОЙ ЗАДАЧИ НА ПРОСТЫЕ;

−          УСТАНОВЛЕНИЕ ОТНОШЕНИЙ МЕЖДУ ЗАДАННЫМИ И ИСКОМЫМИ ВЕЛИЧИНАМИ В ПРОСТЫХ ЗАДАЧАХ;

−               ОПРЕДЕЛЕНИЕ МАТЕМАТИЧЕСКИХ ДЕЙСТВИЙ, СООТВЕТСТВУЮЩИХ ЭТИМ ОТНОШЕНИЯМ, ЧТО ПРИВОДИТ К ПОСЛЕДОВАТЕЛЬНОМУ РЕШЕНИЮ ПРОСТЫХ ЗАДАЧ.

ПРОЦЕСС ОБУЧЕНИЯ РЕШЕНИЮ ЗАДАЧ АРИФМЕТИЧЕСКИМ МЕТОДОМ ВКЛЮЧАЕТ В СЕБЯ ПОСЛЕДОВАТЕЛЬНОЕ УСВОЕНИЕ ДЕТЬМИ СЛЕДУЮЩИХ ДЕЙСТВИЙ:

−                         ЧТЕНИЕ ЗАДАЧИ И ПРЕДСТАВЛЕНИЕ ТОЙ СИТУАЦИИ, КОТОРАЯ В НЕЙ ОПИСАНА;

−                         ВЫДЕЛЕНИЕ В ТЕКСТЕ УСЛОВИЯ И ВОПРОСА, ИЗВЕСТНЫХ И НЕИЗВЕСТНЫХ ЧИСЕЛ ЗАДАЧИ;

−                         УСТАНОВЛЕНИЕ СВЯЗИ МЕЖДУ ДАННЫМИ И ИСКОМЫМИ ЗНА-ЧЕНИЯМИ ВЕЛИЧИН, МОДЕЛИРОВАНИЕ, ЗАДАННОЙ В ТЕКСТЕ СИТУАЦИИ;

−                             ВЫБОР ПОСЛЕДОВАТЕЛЬНОСТИ АРИФМЕТИЧЕСКИХ ДЕЙСТВИЙ, ИСПОЛЬЗУЕМЫХ ДЛЯ РЕШЕНИЯ ЗАДАЧИ, И СОСТАВЛЕНИЕ ПЛАНА РЕШЕНИЯ;

−                              ЗАПИСЬ РЕШЕНИЯ ЗАДАЧИ И ЕЕ ОТВЕТА;

−                              ПРОВЕРКА ПРАВИЛЬНОСТИ РЕШЕНИЯ ЗАДАЧИ И ПОЛУЧЕННОГО ОТВЕТА.

3. ТЕХНОЛОГИЯ ОБУЧЕНИЯ АЛГЕБРАИЧЕСКОМУ МЕТОДУ РЕШЕНИЯ ТЕКСТОВЫХ ЗАДАЧ

ОСОБЕННОСТЬ АЛГЕБРАИЧЕСКОГО МЕТОДА СОСТОИТ В СЛЕДУЮЩЕМ.

1. ВВОДИТСЯ СПЕЦИАЛЬНОЕ ОБОЗНАЧЕНИЕ НЕИЗВЕСТНОЙ ВЕЛИЧИНЫ. ЭТО ПОЗВОЛЯЕТ ДЕЙСТВОВАТЬ С НЕЙ КАК С РЕАЛЬНОЙ, ТО ЕСТЬ ЗАДАННОЙ ВЕЛИЧИНОЙ.

2. ВЫПОЛНЯЕТСЯ АНАЛИЗ ОСНОВНЫХ ЗАВИСИМОСТЕЙ МЕЖДУ ЯВНЫМИ И НЕЯВНЫМИ ЗНАЧЕНИЯМИ ВЕЛИЧИН И ПРОИЗВОДИТСЯ МОДЕЛИРОВАНИЕ УСЛОВИЯ ЗАДАЧИ В ВИДЕ УРАВНЕНИЯ.

РЕШЕНИЕ ЗАДАЧИ АЛГЕБРАИЧЕСКИМ МЕТОДОМ ПРОВОДИТСЯ ПО СЛЕДУЮЩЕМУ АЛГОРИТМУ.

1. ОБОЗНАЧЕНИЕ БУКВОЙ ЗНАЧЕНИЯ НЕИЗВЕСТНОЙ ВЕЛИЧИНЫ.

2. ВЫБОР ОСНОВАНИЯ ДЛЯ СОСТАВЛЕНИЯ УРАВНЕНИЯ.

3. СОСТАВЛЕНИЕ 2-Х ВЫРАЖЕНИЙ (ВОЗМОЖНО ПОЭТАПНОЕ), СЮЖЕТНЫЙ СМЫСЛ КОТОРЫХ СОВПАДАЕТ С ОСНОВАНИЕМ. ЭТИ ВЫРАЖЕНИЯ МОГУТ БЫТЬ ЭЛЕМЕНТАРНЫМИ, ПРОСТЫМИ ИЛИ СОСТАВНЫМИ, НО ОДНО ИЗ НИХ ОБЯЗАТЕЛЬНО БУДЕТ СОДЕРЖАТЬ НЕИЗВЕСТНУЮ ВЕЛИ-ЧИНУ.

4. СОСТАВЛЕНИЕ УРАВНЕНИЯ, ПУТЕМ УСТАНОВЛЕНИЯ РАВЕНСТВА МЕЖДУ ДВУМЯ ВЫРАЖЕНИЯМИ, ИМЕЮЩИМИ ОДИНАКОВЫЙ СЮЖЕТНЫЙ СМЫСЛ ПО ДАННОЙ ЗАДАЧЕ.

5. РЕШЕНИЕ УРАВНЕНИЯ.

6. ПРОВЕРКА ПРАВИЛЬНОСТИ РЕШЕНИЯ ЗАДАЧИ.

ХАРАКТЕРИСТИКА ЭТАПОВ

1 ЭТАП. ОСНОВНАЯ ЗАДАЧА УЧИТЕЛЯ НА ДАННОМ ЭТАПЕ – ДАТЬ ПРЕДСТАВЛЕНИЕ О СЮЖЕТНОМ СМЫСЛЕ ВЫРАЖЕНИЯ, СОСТАВЛЕННОГО ПО ТЕКСТУ ЗАДАЧИ, НАУЧИТЬ ДЕТЕЙ СОСТАВЛЯТЬ ВСЕВОЗМОЖНЫЕ ВЫ-РАЖЕНИЯ ПО ТЕКСТУ ЗАДАЧИ И ОПРЕДЕЛЯТЬ ИХ СЮЖЕТНЫЙ СМЫСЛ.

РЕАЛИЗАЦИЮ ЭТОЙ ЗАДАЧИ МОЖНО ОСУЩЕСТВИТЬ ЧЕРЕЗ СЛЕ-ДУЮЩУЮ СИСТЕМУ ПОСЛЕДОВАТЕЛЬНО УСЛОЖНЯЮЩИХСЯ ЗАДАНИЙ, ТРЕБУЮЩИХ ОТ УЧЕНИКОВ ВСЕ БОЛЬШЕЙ САМОСТОЯТЕЛЬНОСТИ ПРИ ИХ ВЫПОЛНЕНИИ.

1.ДАТЬ ТЕКСТ С ЧИСЛАМИ И, ИСПОЛЬЗУЯ МЕТОД БЕСЕДЫ, СО-СТАВИТЬ ПО ЭТОМУ ТЕКСТУ НЕСКОЛЬКО ВЫРАЖЕНИЙ, ОПРЕДЕЛИТЬ ИХ СМЫСЛ ПО ДАННОМУ СЮЖЕТУ

2. ДАТЬ ТЕКСТ С ЧИСЛАМИ И СОСТАВИТЬ ПО ЭТОМУ ТЕКСТУ НЕ-СКОЛЬКО ВЫРАЖЕНИЙ, А ДЕТЯМ ПРЕДЛОЖИТЬ ОПРЕДЕЛИТЬ ИХ СЮЖЕТНЫЙ СМЫСЛ В СООТВЕТСТВИИ С ДАННЫМ ТЕКСТОМ.

3. ЗАДАНИЕ, ПОДОБНОЕ ПРЕДЫДУЩЕМУ, НО СРЕДИ ВЫРАЖЕНИЙ ДОЛЖНЫ БЫТЬ ТАКИЕ, КОТОРЫЕ НЕ ИМЕЮТ СЮЖЕТНОГО СМЫСЛА ПО ДАННОМУ ТЕКСТУ.

4. ПО ПРЕДЛОЖЕННОМУ ТЕКСТУ С ЧИСЛАМИ ДЕТИ САМОСТОЯТЕЛЬНО СОСТАВЛЯЮТ ВЫРАЖЕНИЯ И ОПРЕДЕЛЯЮТ ИХ СЮЖЕТНЫЙ СМЫСЛ, А ЗАТЕМ, НАХОДЯТ ВЫРАЖЕНИЯ С ОДИНАКОВЫМ СЮЖЕТНЫМ СМЫСЛОМ.

5. ДАТЬ ЗАДАЧУ, РАЗЪЯСНИТЬ СПОСОБ ОБОЗНАЧЕНИЯ НЕИЗВЕСТНОЙ ВЕЛИЧИНЫ ЧЕРЕЗ Х И СПОСОБ СОСТАВЛЕНИЯ ВЫРАЖЕНИИ ПО ЗАДАЧЕ С ИСПОЛЬЗОВАНИЕМ ЭТОЙ НЕИЗВЕСТНОЙ ВЕЛИЧИНЫ КАК ЗАДАННОЙ, ДАЛЕЕ ОПРЕДЕЛИТЬ СЮЖЕТНЫЙ СМЫСЛ ЭТИХ ВЫРАЖЕНИЙ, ОПИРАЯСЬ НА ТЕКСТ ЗАДАЧИ.

6. ПРЕДЛОЖИТЬ ТЕКСТ ЗАДАЧИ, ЗАТЕМ, УЧИТЕЛЬ НАЗЫВАЕТ СЮЖЕТНЫЙ СМЫСЛ ОДНОГО ИЗ ВЫРАЖЕНИЙ, КОТОРОЕ МОЖНО СОСТАВИТЬ ПО ТЕКСТУ ЗАДАЧИ, А ДЕТИ СОСТАВЛЯЮТ ВЫРАЖЕНИЕ, СООТВЕТСТВУЮЩЕЕ ДАННОМУ СЮЖЕТНОМУ СМЫСЛУ.

2 ЭТАП. ОСНОВНОЙ ЗАДАЧЕЙ УЧИТЕЛЯ НА ДАННОМ ЭТАПЕ ЯВЛЯЕТСЯ ВВЕДЕНИЕ ПОНЯТИЯ «ОСНОВАНИЕ ДЛЯ СОСТАВЛЕНИЯ УРАВНЕНИЯ», ВВЕДЕНИЕ АЛГОРИТМА РАССУЖДЕНИЙ И РАЗВЕРНУТОЙ ФОРМЫ ЗАПИСИ РЕШЕНИЯ ЗАДАЧИ АЛГЕБРАИЧЕСКИМ МЕТОДОМ.

ДЕЯТЕЛЬНОСТЬ УЧАЩИХСЯ МОЖЕТ БЫТЬ ОРГАНИЗОВАНА ПО СЛЕДУЮЩЕМУ ПЛАНУ.

1.ДАТЬ ТЕКСТ ЗАДАЧИ

2. ПРЕДЛОЖИТЬ ОБОЗНАЧИТЬ ЧЕРЕЗ Х НЕИЗВЕСТНУЮ ВЕЛИЧИНУ, ЗНАЧЕНИЕ КОТОРОЙ ТРЕБУЕТСЯ НАЙТИ В ВОПРОСЕ ЗАДАЧИ. СОСТАВИТЬ РЯД ВЫРАЖЕНИЙ ПО ТЕКСТУ ЗАДАЧИ И ОПРЕДЕЛИТЬ ИХ СЮЖЕТНЫЙ СМЫСЛ.

3. НАЙТИ ВЫРАЖЕНИЯ С ОДНИМ И ТЕМ ЖЕ СЮЖЕТНЫМ СМЫСЛОМ. СООБЩИТЬ ДЕТЯМ, ЧТО ЕСЛИ ВЫРАЖЕНИЯ, СОСТАВЛЕННЫЕ ПО ТЕКСТУ ОДНОЙ И ТОЙ ЖЕ ЗАДАЧЕ ИМЕЮТ ОДИН И ТОТ ЖЕ СЮЖЕТНЫЙ СМЫСЛ, ТО ОНИ РАВНЫ.

4. СОСТАВИТЬ РАВЕНСТВО ИЗ ДВУХ ВЫРАЖЕНИЙ С ОДИНАКОВЫМ СЮЖЕТНЫМ СМЫСЛОМ, В ОДНО ИЗ КОТОРЫХ ВХОДИТ ПЕРЕМЕННАЯ Х.

5. ВМЕСТЕ С ДЕТЬМИ ОПРЕДЕЛИТЬ, ЧТО ДАННАЯ ЗАПИСЬ В МАТЕМАТИКЕ НАЗЫВАЕТСЯ УРАВНЕНИЕМ.

6. РЕШИТЬ ДАННОЕ УРАВНЕНИЕ И УСТАНОВИТЬ, ЧТО ЗНАЧЕНИЕ Х И ЕСТЬ ОТВЕТ НА ВОПРОС ЗАДАЧИ.

7. СООБЩИТЬ ДЕТЯМ, ЧТО СЮЖЕТНЫЙ СМЫСЛ ВЫРАЖЕНИЙ, КОТОРЫЕ МЫ ИСПОЛЬЗОВАЛИ ПРИ СОСТАВЛЕНИИ УРАВНЕНИЙ, БУДЕМ НАЗЫВАТЬ ОСНОВАНИЕМ ДЛЯ СОСТАВЛЕНИЯ УРАВНЕНИЯ, А МЕТОД РЕШЕНИЯ ЗАДАЧИ, КОТОРЫЙ ИСПОЛЬЗОВАЛСЯ В ДАННОМ СЛУЧАЕ, В МАТЕМАТИКЕ НАЗЫВАЮТ АЛГЕБРАИЧЕСКИМ, ПОСКОЛЬКУ ДЛЯ РЕШЕНИЯ ЗАДАЧИ МЫ ИСПОЛЬЗОВАЛИ АЛГЕБРАИЧЕСКОЕ ПОНЯТИЕ – УРАВНЕНИЕ.

8. ДАЛЕЕ ДЕТЯМ ПРЕДЛАГАЕТСЯ РЕШИТЬ ЕЩЕ ОДНУ ЗАДАЧУ АЛГЕБРАИЧЕСКИМ МЕТОДОМ, ЗАПОМНИТЬ АЛГОРИТМ РАССУЖДЕНИЙ И ПОЛНУЮ ФОРМУ ЗАПИСИ РЕШЕНИЯ ЗАДАЧИ АЛГЕБРАИЧЕСКИМ МЕТОДОМ.

9. РЕШИВ ВТОРУЮ ЗАДАЧУ, УЧИТЕЛЬ ПРЕДЛАГАЕТ УЧАЩИМСЯ ПРОВЕРИТЬ ПРАВИЛЬНОСТЬ РЕШЕНИЯ ЭТОЙ ЗАДАЧИ. ПРЕДЛАГАЕТ ВСПОМНИТЬ ВСЕ ИЗВЕСТНЫЕ ДЕТЯМ СПОСОБЫ ПРОВЕРКИ ПРАВИЛЬНОСТИ РЕШЕНИЯ ЗАДАЧИ, КОТОРЫЕ ИСПОЛЬЗОВАЛИСЬ ДЕТЬМИ РАНЕЕ (СОСТАВЛЕНИЕ И РЕШЕНИЕ ОБРАТНОЙ ЗАДАЧИ, РЕШЕНИЕ ЗАДАЧИ ДРУГИМ СПОСОБОМ, ПРИКИДКА РЕЗУЛЬТАТА И Т.Д.). СООБЩАЕТ ДЕТЯМ НОВЫЙ СПОСОБ ПРОВЕРКИ ПРАВИЛЬНОСТИ РЕШЕНИЯ ЗАДАЧИ, КОТОРЫЙ ИСПОЛЬЗУЕТСЯ В ТОМ СЛУЧАЕ, КОГДА ЗАДАЧА РЕШАЕТСЯ АЛГЕБРАИЧЕСКИМ МЕТОДОМ. СУТЬ ЭТОГО СПОСОБА СОСТОИТ В ТОМ, ЧТО ПО ДАННОЙ ЗАДАЧЕ СОСТАВЛЯЕТСЯ УРАВНЕНИЕ ПО НОВОМУ ОСНОВАНИЮ. ЕСЛИ ПОСЛЕ РЕШЕНИЯ ЭТОГО УРАВНЕНИЯ ПОЛУЧАЕТСЯ ТО ЖЕ САМОЕ ЗНАЧЕНИЕ Х, ЧТО И В ПЕРВОМ УРАВНЕНИИ, ТО ДЕЛАЕТСЯ ЗАКЛЮЧЕНИЕ О ПРАВИЛЬНОСТИ РЕШЕНИЯ ЗАДАЧИ.

10. СОПОСТАВЛЯЯ РЕШЕНИЯ ЗАДАЧ, УЧИТЕЛЬ В ПРОЦЕССЕ ФРОНТАЛЬНОЙ БЕСЕДЫ С ДЕТЬМИ ОБОБЩАЕТ АЛГОРИТМ РЕШЕНИЯ ЗАДАЧ АЛГЕБРАИЧЕСКИМ МЕТОДОМ:

−         ОБОЗНАЧЕНИЕ БУКВОЙ НЕИЗВЕСТНОЙ ВЕЛИЧИНЫ;

−         СОСТАВЛЕНИЕ ВЫРАЖЕНИЙ;

−         ВЫБОР ОСНОВАНИЯ ДЛЯ СОСТАВЛЕНИЯ УРАВНЕНИЯ;

−         СОСТАВЛЕНИЕ УРАВНЕНИЯ;

−         РЕШЕНИЕ УРАВНЕНИЯ;

−         ПРОВЕРКА ПРАВИЛЬНОСТИ РЕШЕНИЯ ЗАДАЧИ

3 ЭТАП. ЗАКРЕПЛЕНИЕ МАТЕРИАЛА. ОСНОВНЫЕ ЗАДАЧИ ЭТОГО ЭТАПА: ОБЕСПЕЧИТЬ ОСОЗНАННОЕ ВЫПОЛНЕНИЕ КАЖДОГО ПУНКТА АЛГО-РИТМА РЕШЕНИЯ ЗАДАЧАМ, ПОСТЕПЕННО УВЕЛИЧИВАЯ ДОЛЮ САМОСТОЯТЕЛЬНОСТИ В ЕГО ВЫПОЛНЕНИИ, ПЕРЕЙТИ ОТ РАЗВЕРНУТОЙ ЗАПИСИ ВСЕГО ПРОЦЕССА РАССУЖДЕНИЙ К СОКРАЩЕННОЙ, СФОРМИРОВАТЬ УМЕ-НИЕ ОСУЩЕСТВЛЯТЬ САМОКОНТРОЛЬ И ВЗАИМОКОНТРОЛЬ ЗА ПРАВИЛЬ-НОСТЬЮ ВЫПОЛНЕНИЯ КАЖДОГО ПУНКТА ПЛАНА.

РЕАЛИЗАЦИЯ ЗАДАЧ, СТОЯЩИХ НА ДАННОМ ЭТАПЕ ОБУЧЕНИЯ РЕШЕНИЮ ЗАДАЧ АЛГЕБРАИЧЕСКИМ МЕТОДОМ, МОЖЕТ БЫТЬ ДОСТИГНУТА ПУТЕМ ИСПОЛЬЗОВАНИЯ СЛЕДУЮЩИХ ПРИЕМОВ:

−        ОРГАНИЗАЦИЯ ФРОНТАЛЬНОЙ БЕСЕДЫ С ИСПОЛЬЗОВАНИЕМ СИСТЕМЫ ЦЕЛЕСООБРАЗНО ПОДОБРАННЫХ ВОПРОСОВ, НАПРАВЛЕННЫХ НА ВЫЯВЛЕНИЕ СТЕПЕНИ ОСОЗНАННОСТИ ДЕЙСТВИЙ, ОСУЩЕСТВЛЯЕМЫХ НА КАЖДОМ ЭТАПЕ АЛГОРИТМА РЕШЕНИЯ ЗАДАЧ АЛГЕБРАИЧЕСКИМ МЕТОДОМ;

−        ОРГАНИЗАЦИЮ ГРУППОВОЙ РАБОТЫ, ПРЕДПОЛАГАЮЩЕЙ ПОИСК И ЗАЩИТУ ПРАВИЛЬНОСТИ ПРОДЕЛАННЫХ ГРУППОЙ ДЕЙСТВИЙ ПРИВОДЯЩИХ К РЕШЕНИЮ ЗАДАЧИ АЛГЕБРАИЧЕСКИМ МЕТОДОМ;

−        ПОДБОР ПОСТЕПЕННО УСЛОЖНЯЮЩИХСЯ ЗАДАНИЙ, ОБЕСПЕЧИВАЮЩИХ ОТРАБОТКУ ВСЕХ ДЕЙСТВИЙ, ВХОДЯЩИХ В СОСТАВ СПОСОБА РЕШЕНИЯ ЗАДАЧ АЛГЕБРАИЧЕСКИМ МЕТОДОМ.