Задачи оптимизации в Excel

Задачи оптимизации в Excel

Пример решения задачи по теории игр

ЗАДАНИЕ.  

Намечается крупномасштабное производство легковых автомобилей. Имеются четыре варианта проекта автомобиля Rj. Определена экономическая эффективность К - каждого проекта в зависимости от рентабельности производства. По истечении трех сроков Si рассматриваются как некоторые состояния среды (природы). Значения экономической эффективности для различных проектов и состояний природы приведены в следующей таблице (д. е.):

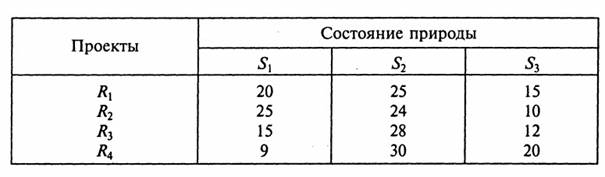
Выберите оптимальное решение в соответствии с критериями Лапласа, Вальда, Сэвиджа и Гурвица (при а = 0,5).

РЕШЕНИЕ.  

Критерий пессимизма-оптимизма Лапласа.

В основе критерия лежит предположение: поскольку о состояниях обстановки ничего не известно, то их можно считать равновероятными.

Если статистик не располагает объективной информацией об априорных вероятностях q_j состояний природы П_j и считает в равной мере правдоподобными все состояния, то их вероятности полагают одинаковыми, т. е. q₁ = … = q_n = 1/n.

∑aij q j

20

19,66666667

18,33333333

19,66666667

q                            0,333333         0,333333         0,333333                                    

Оптимальное решение по данному критерию – проект R1

Критерий Вальда

Так как в данном примере a_ij представляет эффективность, т.е. выигрыш, то применяется максиминный критерий.

Критерий основывается на том, что если состояние обстановки неизвестно, нужно поступать самым осторожным образом, ориентируясь на минимальное значение эффективности каждой системы.

min a

ij

15

10

12

9

Из минимальных значений выбираем максимальное. 

Оптимальное решение по данному критерию – проект R1

Критерий минимального риска (Сэвиджа). 

Минимизирует потери эффективности при наихудших условиях. 

Для оценки систем на основе данного критерия матрица эффективности должна быть преобразовании в матрицу потерь (риска). 

Каждый элемент матрицы потерь определяется как разность между максимальным и текущим значениями оценок эффективности в столбце:

                                                                            ∆       =                   −       .

После преобразования матрицы используется критерий минимакса

Критерий пессимизма-оптимизма Гурвица.

Это критерий обобщённого максимина.

Для этого вводится коэффициент оптимизма α (0 ≤ α ≤ 1), характеризующий отношение к риску лица, принимающего решение. 

Эффективность систем находится как взвешенная с помощью коэффициента α (выбирается из субъективных соображений) сумма максимальной и минимальной оценок.

При α = 0 критерий Гурвица превращается в критерий Вальда При α = 1 – в критерий крайнего оптимизма При 0 < α < 1 получается нечто среднее.

H = max{αmax a_ij +(1−α)min a_ij }

                                                                                          maxa_ij                                                         min a_ij αmax a_ij + (1−α)min a_ij

                                                                                        15                   25          20

                                                                                        10                   25          17,5

                                                                                        12                   28          20

                                                                                        9                     30          19,5

Оптимальное решение по данному критерию – проект R1 По всем критериям рекомендовался выбор проекта R1