Задачи оптимизации в Excel
Задача о кондитерских изделиях
ЗАДАНИЕ.
Для изготовления одного пирожка требуется 0,8 ед. начинки и 4 ед. теста, одного пирожного 4 ед. начинки и 0,5 ед. теста, одного рулета 2 ед. начинки и 2,5 ед. теста. Сколько пирожков, пирожных и рулетов нужно сделать кондитерской, если в наличии имеется 120 ед. теста и 300 ед. начинки? Определите доход от реализации кондитерских изделий, если доход от продажи одного пирожка составляет 3 рубля, одного пирожного 2 рубля, одного рулета 1,5.
Для решения задачи используется ППП Excel.
РЕШЕНИЕ.
Пусть x1 - количество изготавливаемых пирожков, x2 - количество изготавливаемых пирожных, x3 - количество рулетов.
Для приготовления изделий используется 0.8x1 + 4x2 + 2x3 единиц начинки и
4x1 + 0.5x2 + 2.5x3 единиц теста.
Очевидно, что количество используемых начинки и теста не может превышать имеющийся в наличии запас, поэтому:
0.8x1 + 4x2 + 2x3 ≤ 300
4x1 + 0.5x2 + 2.5x3 ≤ 120
Кроме того количество изготавливаемых пирожков, пирожных и рулетов не может быть отрицательным числом, т.е.: x1 ≥ 0,x2 ≥ 0,x3 ≥ 0
Кроме того, количество кондитерских изделий должно быть целым числом:
x1,x2,x3−целые
Доход от реализации изделий составит: 3x1 + 2x2 +1.5x3. Цель предприятия – увеличение дохода, поэтому Z = 3x1 + 2x2 +1.5x3 → max
Получили математическую модель задачи
Z = 3x1 + 2x2 +1.5x3 → max
При условиях
0.8x1 + 4x2 + 2x3 ≤ 300 4x1 + 0.5x2 + 2.5x3 ≤ 120 x1 ≥ 0,x2 ≥ 0,x3 ≥ 0 x1,x2,x3−целые
Решим задачу с помощью EXCEL
В целях нахождения решения задачи с помощью этого модуля предварительно составим в книге Microsoft Excel форму, содержащую исходные данные.
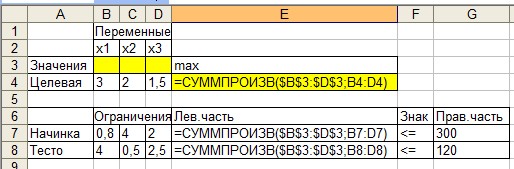
Количество соответствующих переменных предполагаем получить в ячейках В3:D3. В ячейке E4 введена формула, по которой будет рассчитан доход от реализации. В ячейках Е7: Е8 введены формулы для расчета значений левой части ограничений.
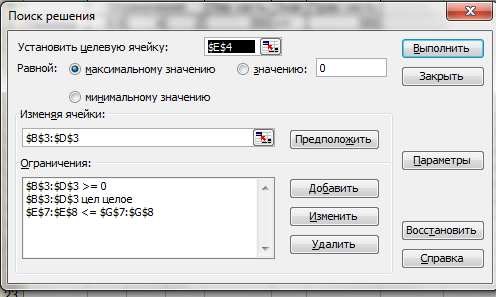
Запускаем процедуру оптимизации. В меню Сервис выбираем пункт Поиск решения.
В поле Установить целевую ячейку вводим координаты ячейки Е4, которую необходимо максисизировать. Поле нужного варианта оптимизации выделяем указателем.
В поле Изменяя ячейки вводим координаты ячеек, в которых содержатся значения переменных.
В поле Ограничения вводим все граничные условия задачи.
Отмечаем в окне Параметры соответствующим флажком, что решаемая задача является задачей линейного программирования:
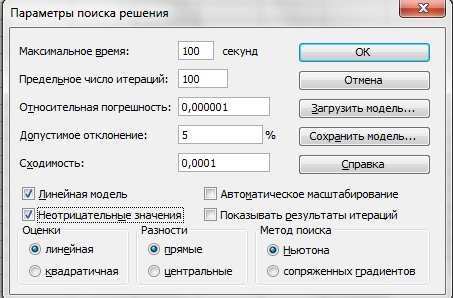
Запускаем процесс оптимизации нажатием кнопки Выполнить.
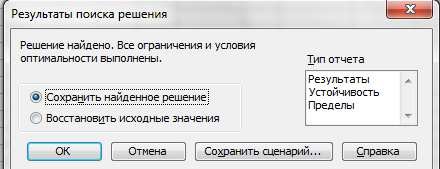
Полученные результаты решения рассматриваемой задачи выглядят так:
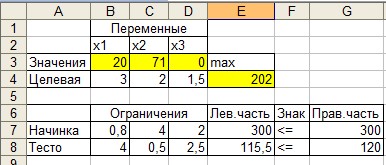
Итак, максимальный доход составит 205 руб. Для этого надо изготавливать: 20 пирожков и 71 пирожное, рулеты изготавливать не надо.
При данном плане выпуска останется недоиспользованным тесто в количестве 4,5ед.
Задачи оптимизации в Excel
Доход от реализации изделий составит: 3 x 1 + 2 x 2 + 1
В поле Установить целевую ячейку вводим координаты ячейки
Полученные результаты решения рассматриваемой задачи выглядят так:
© ООО «Знанио»
С вами с 2009 года.
