Задачи с решениями по теме "Окружность".

Задача 1. Правильный треугольник ABC со стороной, равной 3, вписан в окружность. Точка D лежит на окружности, причем длина хорды AD равна  (рис. 10). Найти длины хорд BD и CD.

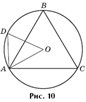
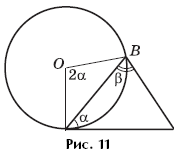
Задача 2. Окружность радиуса R проходит через вершины A и B треугольника ABC и касается прямой AC в точке A (рис. 11). Найти площадь треугольника ABC, зная, что ∠ABC = β, ∠CAB = α.

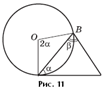
Задача 3. Вокруг треугольника ABC описана окружность. Медиана AD продолжена до пересечения с этой окружностью в точке E (рис. 12). Известно, что AB + AD = DE, угол BAD равен 60° и AE = 6. Найти площадь треугольника ABC.

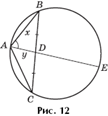
Задача 4. На стороне AC остроугольного треугольника ABC взята точка D так, что AD=1, DC = 2 и BD является высотой треугольника ABC. Окружность радиуса 2, проходящая через точки A и D, касается в точке D окружности, описанной около треугольника BDC (рис. 13). Найти площадь треугольника ABC.

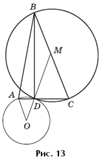
Задача 5. Дан треугольник ABC, в котором BC = 5. Окружность проходит через вершины B и C и пересекает сторону AC в точке K так, что CK = 3, KA = 1. Известно, что косинус угла ACB равен  (рис. 14). Найти отношение радиуса данной окружности к радиусу окружности, вписанной в треугольник ABK.

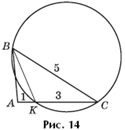
Задача 6. В треугольнике ABC известны стороны AB = 6, BC = 4, AC = 8. Биссектриса угла C пересекает сторону AB в точке D. Через точки A, D, C проведена окружность, пересекающая сторону BC в точке E (рис. 15). Найти площадь треугольника ADE.

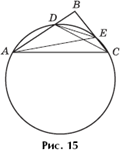
Задача 7. Вокруг треугольника ABC со сторонами  AC = 20 и углом B, равным 45°, описана окружность. Через точку C проведена касательная к окружности, пересекающая продолжение стороны AB за точку A в точке D (рис. 16). Найти площадь треугольника BCD.

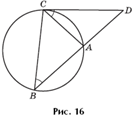
Задача 8. В окружность радиуса 17 вписан четырехугольник, диагонали которого взаимно перпендикулярны и находятся на расстоянии 8 и 9 от центра окружности (рис. 17). Найти длины сторон четырехугольника.

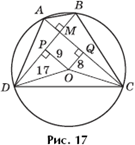
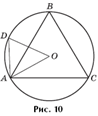
Задача 9. Пятиугольник ABCDE вписан в окружность единичного радиуса (рис. 18). Известно, что  и BC = CD. Чему равна площадь пятиугольника?

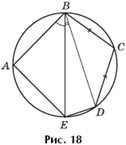
Задача 10. Выпуклый четырехугольник ABCD вписан в окружность. Диагональ AC является биссектрисой угла BAD и пересекается с диагональю BD в точке K (рис. 19). Найти длину отрезка KC, если BC = 4, а AK = 6.

Решения задач № 1-10 (разбор, ответ)

Задача 1. Правильный треугольник ABC со стороной, равной 3, вписан в окружность. Точка D лежит на окружности, причем длина хорды AD равна  (рис. 10). Найти длины хорд BD и CD.

Решение.

Легко видеть, что радиус окружности, описанной около правильного треугольника со стороной a, равен Значит, радиус данной окружности равен . Пусть O — центр данной окружности. В треугольнике AOD все стороны равны. Поэтому ∠DAO = 60°. Кроме того, так как треугольник ABC — правильный, то ∠OAC = 30°.
Значит, ∠DAC = 90°, и треугольник DAC — прямоугольный. Следовательно, CD — диаметр окружности, и  Значит, и треугольник BCD прямоугольный, откуда по теореме Пифагора находим, что  Ясно, что при переобозначении точек B и C получим, что 

Ответ:  и 

Задача 2. Окружность радиуса R проходит через вершины A и B треугольника ABC и касается прямой AC в точке A (рис. 11). Найти площадь треугольника ABC, зная, что ∠ABC = β, ∠CAB = α.

Решение. Угол α между касательной AC и хордой AB, выходящими из точки A окружности, равен половине угловой величины дуги AB и, значит, равен любому вписанному углу, опирающемуся на ту же дугу. Поэтому мы можем применить теорему синусов: AB = 2Rsin α.
Рассмотрим треугольник ABC, к которому также применим теорему синусов:

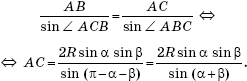
Следовательно,

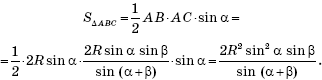
Ответ: 

Задача 3. Вокруг треугольника ABC описана окружность. Медиана AD продолжена до пересечения с этой окружностью в точке E (рис. 12). Известно, что AB + AD = DE, угол BAD равен 60° и AE = 6. Найти площадь треугольника ABC.

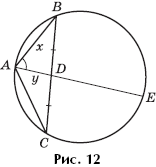
Решение. Пусть AB = x, AD = y, тогда, согласно условию задачи, DE = x + y. Так как в окружности произведения отрезков двух пересекающихся хорд равны, имеем:
AD∙DE = BD∙DC ⇔ 
Применим к треугольнику ABD теорему косинусов:
BD² = AB² + AD² – 2AB∙AD∙cos ∠BAD ⇔
⇔ ⇔ x2 = 2xy ⇔ x = 2y.
Условие AE = 6 дает равенство x + 2y = 6. Подставляя в него x = 2y, находим:  x = 3. Искомая площадь равна 

Ответ: 

Задача 4. На стороне AC остроугольного треугольника ABC взята точка D так, что AD = 1,
DC = 2 и BD является высотой треугольника ABC. Окружность радиуса 2, проходящая через точки A и D, касается в точке D окружности, описанной около треугольника BDC (рис. 13). Найти площадь треугольника ABC.

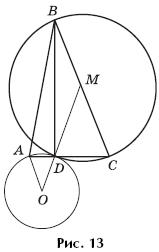
Решение. Треугольник BCD — прямоугольный, поэтому центр описанной около него окружности есть середина M стороны BC. Пусть O — центр окружности радиуса 2, проходящей через A и D. Так как данные окружности касаются, то точки O, D, M лежат на одной прямой. А из равенства углов ADO и CDM, в силу равнобедренности треугольников ADO и CDM, следует подобие этих треугольников. Значит, DM = 4 и BC = 2 DM = 8.Применив теорему Пифагора к треугольнику BCD, получим, что  Следовательно,

Ответ: 

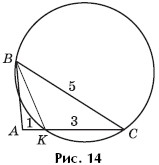
Задача 5. Дан треугольник ABC, в котором
BC = 5. Окружность проходит через вершины B и C и пересекает сторону AC в точке K так, что
CK = 3, KA = 1. Известно, что косинус угла ACB равен  (рис. 14). Найти отношение радиуса данной окружности к радиусу окружности, вписанной в треугольник ABK.

Решение. Применим к треугольнику ABC теорему косинусов:
AB² = BC² + AC² – 2BC∙AC∙cos ∠ACB = 9 ⇒
⇒ AB = 3.
Следовательно, треугольник ABC — прямоугольный (так как его стороны равны 3, 4, 5). Треугольник ABK также прямоугольный, применив к нему теорему Пифагора, получим, что  Значит, радиус вписанной в треугольник ABK окружности равен

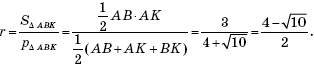
Окружность, данная в условии задачи, описана около треугольника BCK. По теореме синусов ее радиус равен

Тогда искомое отношение равно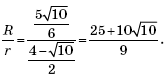 

Ответ: 

Задача 6. В треугольнике ABC известны стороны AB = 6, BC = 4, AC = 8. Биссектриса угла C
пересекает сторону AB в точке D. Через точки A, D, C проведена окружность, пересекающая сторону BC в точке E (рис. 15). Найти площадь треугольника ADE.

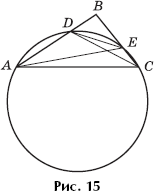
Решение. Биссектриса CD угла ACB делит сторону AB на отрезки, пропорциональные прилежащим сторонам, поэтому AD = 4 и BD = 2. Далее, углы DAE и DCE равны, как опирающиеся на одну и ту же дугу, и аналогично равны углы AED и ACD. Но ∠ACD = ∠DCE, поэтому все четыре названных угла равны. Следовательно, треугольник ADE — равнобедренный и DE = 4.
Найдем синус угла ADE. Так как четырехугольник ADEC вписан в окружность, то
∠ADE + ∠ACE = 180°, sin ∠ADE = sin ∠ACE.
Применим к треугольнику ABC теорему косинусов:

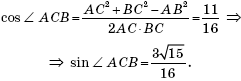
Значит, 

Ответ: 

Задача 7. Вокруг треугольника ABC со сторонами  AC = 20 и углом B, равным 45°, описана окружность. Через точку C проведена касательная к окружности, пересекающая продолжение стороны AB за точку A в точке D (рис. 16). Найти площадь треугольника BCD.

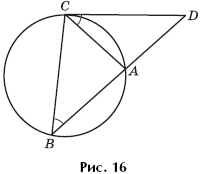
Решение. Угол ABC равен половине угловой величины дуги AC, как вписанный угол, опирающийся на эту дугу. Угол ACD также равен половине угловой величины дуги AC, как угол между касательной и хордой. Следовательно, эти углы равны, и треугольники DBC и DCA подобны по двум углам. Площади этих треугольников относятся как квадрат коэффициента подобия. Найдем этот коэффициент, он равен BC : AC. Пусть BC = 10x, тогда, применив к треугольнику ABC теорему косинусов, получим:

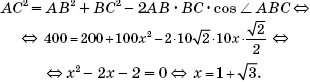
Значит, 

Поэтому



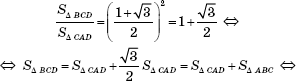
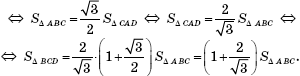
С другой стороны, легко вычислить

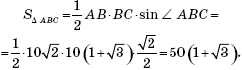
Значит, 

Ответ: 

Задача 8. В окружность радиуса 17 вписан четырехугольник, диагонали которого взаимно перпендикулярны и находятся на расстоянии 8 и 9 от центра окружности (рис. 17). Найти длины сторон четырехугольника.

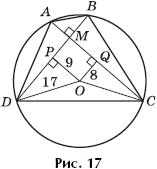
Решение. Обозначим исходный четырех­угольник через ABCD таким образом, чтобы точка B лежала на меньшей дуге AC, а точка A лежала на меньшей дуге BD. Пусть O — центр окружности, OQ и OP — перпендикуляры, опущенные из центра окружности на хорды AC и BD соответственно, M — точка пересечения AC и BD. Тогда AQ = QC, BP = PD, OQMP — прямоугольник со сторонами OQ = PM = 8 и
OP = QM = 9. Применим к треугольнику COQ теорему Пифагора:

Аналогично из треугольника ODP получим, что

Значит,

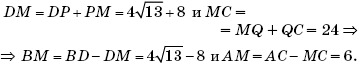
Находим стороны четырехугольника ABCD, пользуясь теоремой Пифагора:

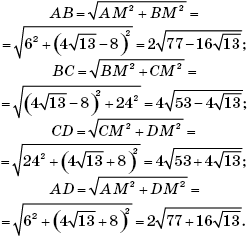
Ответ: 

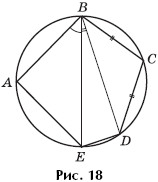
Задача 9. Пятиугольник ABCDE вписан в окружность единичного радиуса (рис. 18).
Известно, что  и BC = CD. Чему равна площадь пятиугольника?

Решение. Пусть O — центр данной окружности. Так как стороны треугольника AOB равны 1, 1 и  то этот треугольник прямоугольный, и угол AOB равен . Поскольку угол ABE равен , то угол AOE также равен , и BE — диаметр окружности. Угол EBD равен  следовательно, угол EOD равен  а так как BC = CD, то 
Итак, пятиугольник ABCDE состоит из двух прямоугольных и трех равносторонних треугольников. Его площадь равна

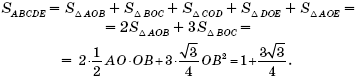
Ответ: 

Задача 10. Выпуклый четырехугольник ABCD вписан в окружность. Диагональ AC является биссектрисой угла BAD и пересекается с диагональю BD в точке K (рис. 19). Найти длину отрезка KC, если BC = 4, а AK = 6.

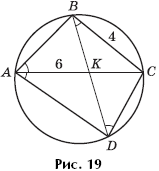
Решение. Так как AC — биссектриса угла BAD, то угол BAC равен углу CAD. С другой стороны, углы CAD и CBD равны (как вписанные, опирающиеся на одну и ту же дугу). Значит, угол BAC равен углу CBK. Следовательно, треугольник ABC подобен треугольнику BCK (по двум углам). Имеем: 

Ответ: 2.