Задание 22 (ОГЭ)

Задачи на проценты, сплавы и смеси:

1.      Смешав 60%−ый и 30%−ый растворы кислоты и добавив 5 кг чистой воды, получили 20%−ый раствор кислоты. Если бы вместо 5 кг воды добавили 5 кг 90%−го раствора той же кислоты, то получили бы 70%−ый раствор кислоты. Сколько килограммов 60%−го раствора использовали для получения смеси?

          Решение:

Пусть x кг и y кг — массы первого и второго растворов, взятые при смешивании. Тогда х+у+5 кг — масса полученного раствора, содержащего 0,6х+0,3у кг кислоты. Концентрация кислоты в полученном растворе 20%, откуда

Решим систему двух полученных уравнений:

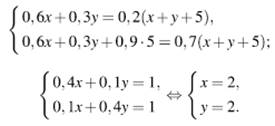
     Ответ: 2 кг.

2.      Име­ет­ся два спла­ва с раз­ным со­дер­жа­ни­ем меди: в пер­вом со­дер­жит­ся 60%, а во вто­ром — 45% меди. В каком от­но­ше­нии надо взять пер­вый и вто­рой спла­вы, чтобы по­лу­чить из них новый сплав, со­дер­жа­щий 55% меди?

Ответ: 2:1

3.      Свежие фрукты содержат 80% воды, а высушенные — 28%. Сколько сухих фруктов получится из 288 кг свежих фруктов?

Ответ: 80 кг

4.      Имеются два сосуда, содержащие 4 кг и 16 кг раствора кислоты различной концентрации. Если их слить вместе, то получится раствор, содержащий 57% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 60% кислоты. Сколько килограммов кислоты содержится в первом растворе?

Ответ: 2,6 кг

Задачи на движение по прямой:

1.      Из пунк­тов А и В, рас­сто­я­ние между ко­то­ры­ми 19 км, вышли од­но­вре­мен­но нав­стре­чу друг другу два пе­ше­хо­да и встре­ти­лись в 9 км от А. Най­ди­те ско­рость пешехода, шед­ше­го из А, если известно, что он шёл со скоростью, на 1 км/ч большей, чем пешеход, шед­ший из В, и сде­лал в пути по­лу­ча­со­вую остановку.

        Решение:

Пусть скорость пешехода, шедшего из пункта A, равна х км/ч, х>1. Тогда скорость пешехода, шедшего из пункта B, равна (х-1) км/ч.   Составим таблицу по данным задачи:

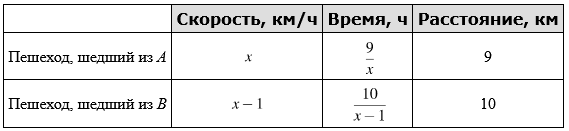
Так как пешеход, шедший из A, сделал по пути остановку на  ч., а вышли пешеходы одновременно, можно составить следующее уравнение:

Ответ: 6 км/ч.

2.      Расстояние между го­ро­да­ми А и В равно 490 км. Из го­ро­да А в город В со ско­ро­стью 55 км/ч вы­ехал пер­вый автомобиль, а через час после этого нав­стре­чу ему из го­ро­да В вы­ехал со ско­ро­стью 90 км/ч вто­рой автомобиль. На каком рас­сто­я­нии от го­ро­да А ав­то­мо­би­ли встретятся?

Ответ: 220 км

3.      Из пунк­та А в пункт В, рас­сто­я­ние между ко­то­ры­ми 13 км, вышел пе­ше­ход. Од­но­вре­мен­но с ним из В в А вы­ехал ве­ло­си­пе­дист. Ве­ло­си­пе­дист ехал со ско­ро­стью, на 11 км/ч боль­шей ско­ро­сти пе­ше­хо­да, и сде­лал в пути по­лу­ча­со­вую оста­нов­ку. Най­ди­те ско­рость пе­ше­хо­да, если из­вест­но, что они встре­ти­лись в 8 км от пунк­та В.

Ответ: 5 км/ч

4.      Два че­ло­ве­ка од­но­вре­мен­но от­прав­ля­ют­ся из од­но­го и того же места по одной до­ро­ге на про­гул­ку до опуш­ки леса, на­хо­дя­щей­ся в 3,7 км от места от­прав­ле­ния. Один идёт со ско­ро­стью 3,3 км/ч, а дру­гой — со ско­ро­стью 4,1 км/ч. Дойдя до опуш­ки, вто­рой с той же ско­ро­стью воз­вра­ща­ет­ся об­рат­но. На каком рас­сто­я­нии от точки от­прав­ле­ния про­изойдёт их встре­ча?        Ответ: 3,3 км

Задачи на движение по воде:

1.      Расстояние между при­ста­ня­ми А и В равно 80 км. Из А в В по те­че­нию реки от­пра­вил­ся плот, а через 2 часа вслед за ним от­пра­ви­лась яхта, которая, при­быв в пункт В, тот­час по­вер­ну­ла об­рат­но и воз­вра­ти­лась в А. К этому вре­ме­ни плот про­шел 22 км. Най­ди­те ско­рость яхты в не­по­движ­ной воде, если ско­рость те­че­ния реки равна 2 км/ч. Ответ дайте в км/ч.

            Решение.

Пусть искомая скорость равна v км/ч, v > 2. Cоставим таблицу по данным задачи:

      Таким образом, скорость яхты в неподвижной воде равна 18 км/ч.
     Ответ: 18 км/ч.

2.      Ту­ри­сты про­плы­ли на лодке от ла­ге­ря не­ко­то­рое рас­сто­я­ние вверх по те­че­нию реки, затем при­ча­ли­ли к бе­ре­гу и, по­гу­ляв 2 часа, вер­ну­лись об­рат­но через 6 часов от на­ча­ла пу­те­ше­ствия. На какое рас­сто­я­ние от ла­ге­ря они от­плы­ли, если ско­рость те­че­ния реки равна 3 км/ч, а соб­ствен­ная ско­рость лодки 6 км/ч?

Ответ: 9 км

3.      От при­ста­ни А к при­ста­ни В, рас­сто­я­ние между ко­то­ры­ми равно 153 км, от­пра­вил­ся с по­сто­ян­ной ско­ро­стью пер­вый теп­ло­ход, а через 4 часа после этого сле­дом за ним, со ско­ро­стью, на 16 км/ч боль­шей, от­пра­вил­ся вто­рой. Най­ди­те ско­рость пер­во­го теп­ло­хо­да, если в пункт В оба теп­ло­хо­да при­бы­ли од­но­вре­мен­но.

Ответ:18 км/ч

Задачи на совместную работу:

1.      На из­го­тов­ле­ние 231 де­та­ли уче­ник тра­тит на 11 часов больше, чем ма­стер на из­го­тов­ле­ние 462 таких же деталей. Известно, что уче­ник за час де­ла­ет на 4 де­та­ли меньше, чем мастер. Сколь­ко де­та­лей в час де­ла­ет ученик?

Решение.

Предположим, что ученик делает х деталей в час, x>1. Тогда мастер делает х+4 детали в час.

Составим таблицу по данным задачи:

Корни полученного квадратного уравнения: −28 и 3. Отбрасывая отрицательный корень, находим, что ученик делает в час 3 детали.

Ответ: 3.

2.      Дима и Саша вы­пол­ня­ют оди­на­ко­вый тест. Дима от­ве­ча­ет за час на 12 во­про­сов теста, а Саша — на 22. Они од­но­вре­мен­но на­ча­ли от­ве­чать на во­про­сы теста, и Дима за­кон­чил свой тест позже Саши на 75 минут. Сколь­ко во­про­сов со­дер­жит тест?

Ответ: 33

3.      Две трубы на­пол­ня­ют бас­сейн за 8 часов 45 минут, а одна пер­вая труба на­пол­ня­ет бас­сейн за 21 час. За сколь­ко часов на­пол­ня­ет бас­сейн одна вто­рая труба?

Ответ: 15 ч