Замечательные свойства трапеции

I.Замечательные отрезки в трапеции.

Для начала я обозначу некоторые очень важные факты об отрезках в трапеции.

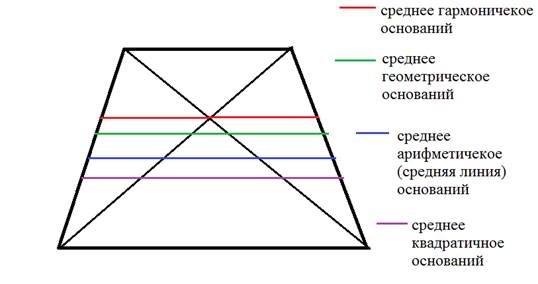
1.     Во всякой трапеции середины оснований, точка пересечения диагоналей и точка пересечения продолжения боковых сторон лежат на одной прямой.

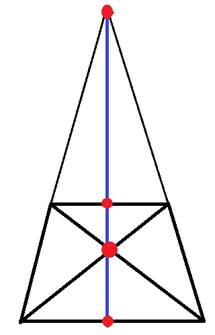
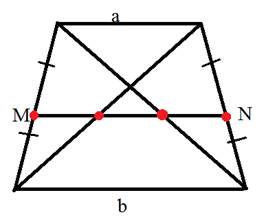
2.     Во всякой трапеции середины боковых сторон и середины диагоналей лежат на одной прямой, называемой средней линией трапеции или среднем арифметическим оснований.

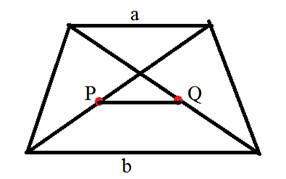
3.     Отрезок, соединяющий середины диагоналей трапеции, равен полуразности оснований.

4.     Отрезок, параллельный основаниям и разбивающий трапецию на две равновеликие трапеции, равен среднему квадратичному оснований:

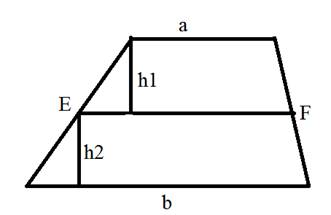
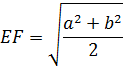
5.     Отрезок,разбивающий трапецию на две подобные трапеции, имеет длину, равную среднему геометрическому длин оснований.

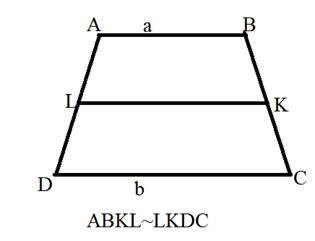
6.      Отрезок, проходящий через точку пересечения диагоналей параллельно основаниям, равен среднему гармоническому оснований.

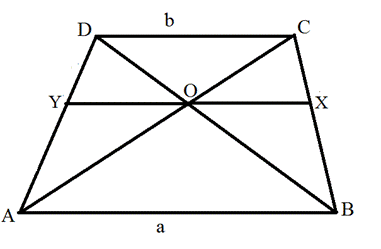
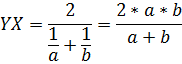
Между средними отрезками выполняются следующие соотношения

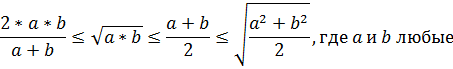
Доказательства этих фактов я не считаю нужным и уместным приводить в докладе, так как любой уважающий себя школьник должен их знать и уметь делать самостоятельно

Теперь, когда мы знаем эти, весьма важные, факты преступим к решению поистине прекрасных задач.

Задача 1:ABCD- трапеция, отрезок MN параллелен основаниям трапеции; AD=11,BC=3,MN=8.Может  ли быть x:y=4:3?

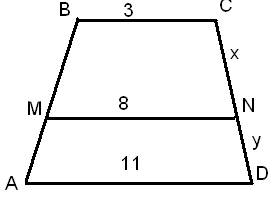
Решение:

Применим приём достраивания.

Построим CF║BA, NE║BA. По построению MBCF и AMNE- параллелограммы, тогда имеем MF=3,FN=5,AE=8 и ED=3.

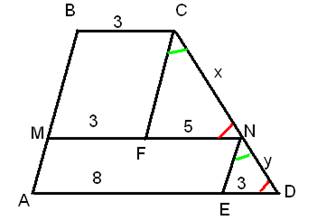
Рассмотрим ∆FCN ~∆END( ∟FCN=∟END, ∟FNC=∟EDN, как накрестлежащие). Из подобия следует, что x:y=5:3, следовательно такого соотношения, как указанно в условии не может быть.

Ответ: не может быть.

Задача 2

ABCD- трапеция,MN║AD, MN=4; точка О ,пересечения диагоналей, находится вдвое дальше от меньшего основания, чем от средней линии. Чему равны основания трапеции?

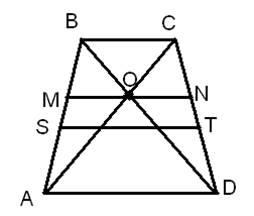
Решение

ПустьAD=a, BC=b.

1.      Из 6 свойства трапеции, а именно, отрезок , проходящий через точку пересечения диагоналей параллельно основаниям, равен среднему гармоническому длин оснований трапеции. Следовательно, MN=.

2.     Пусть ST- средняя линия и через точку О проведена прямая EF, перпендикулярная к основаниям.

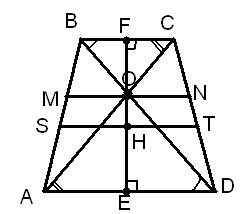
EF- высота трапеции, обозначим EF=h. Очевидно, что средняя линия делит высоту трапеции пополам EH=FH=h

∆BOC~∆DOA(по двум накрестлежащим углам)→

∆OFC~∆OEA(по двум углам)→

FO+OE=h, OE=, тогда находим FO=. По условию FH=FO+½FO=FO, следовательноFO= и тогда , откуда имеем a=2b.

3.    Подставляем a=2b в равенство , находим b=3 и а=6.

Ответ: a=6;b=3.

II Метод площадей

Для того, чтобы решать задачи, где рассматривается площадь трапеции, необходимо помнить несколько очень важных утверждений:

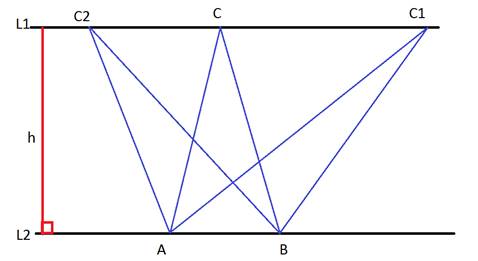
1.Если прямаяL1║L2, то S∆_ABC=S∆_AC1B=S∆_AC2B.

Доказательство:

Это очень легко доказать: площадь треугольника можно вычислить по формуле . Высоты у всех треугольников одинаковы, так как расстояние между параллельными прямыми всегда одинаково; треугольники имеют общее основание. Из этих двух фактов следует, что S∆_ABC=S∆_AC1B=S∆_AC2B.

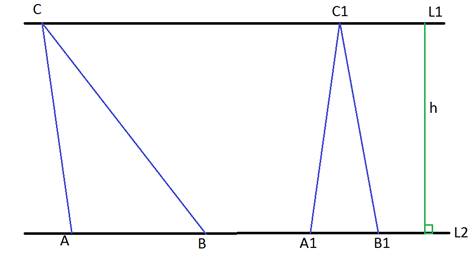
2.Если прямаяL1║L2 и треугольники не имеют общегооснования,  то

 .

Доказательство:

 Высоты у этих треугольников равные, следовательно, площади этих треугольников относятся, как их снования.

А сейчас немного отвлечёмся от трапеции и перенесёмся в треугольник. Возьмём на рассмотрение одну очень красивую и важную задачу, которая поможет  нам в понимании следующей задачи с трапецией. Когда я первый раз увидела эту задачу , она мне сразу же понравилась своей изящностью рисунка и простой гениальностью решения.

Задача 3:

Через точку М, лежащую внутри треугольника АВС проведены три прямые, параллельные его сторонам. При этом образовались три треугольника(см.рис.), площади которых равны S1,S2,S3. Найдите площадь треугольника АВС.

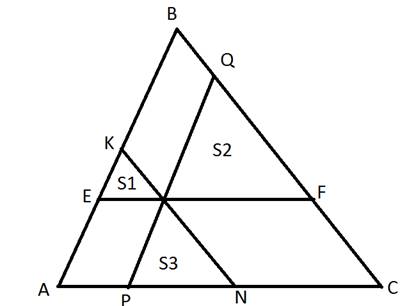
Решение:

Легко видеть, что ∆EKM,∆MQF и ∆PMNподобны ∆АВС. Пусть Sплощадь треугольника АВС, тогда ;; .

Отсюда находим

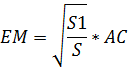
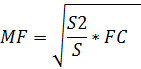
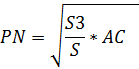
Так какEM=AP, MF=NC , тоEM+PN+MF=AP+PN+NC=AC. Таким образом ,, откуда следует

Ответ:

Мне захотелось убедиться, возможно ли в трапеции  похожее соотношение площадей. И действительно в трапеции нашёлся похожий случай. Рассмотрим его в следующей задачи.

Задача 4:

Дана трапеция ABCD; в трапеции проведены диагонали, пересекающиеся в точке О. Выразите площадь трапеции из площадей образовавшихся треугольников.

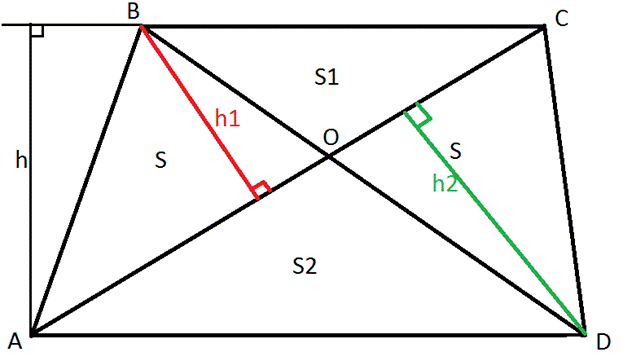
Решение:

1.Пусть площадь ∆AOB и ∆CODравныS. Площадь треугольника BOC равна S1 ,  а площадь треугольника DOA равна S2.

2. Докажем, что S∆_AOB=S∆_COD.

∆ABC и ∆DBC имеют общее основание BCи общую высотуh (т.к.BC║AD по свойству трапеции). Поскольку мы уже знаем , что треугольники имеющие общее основание и высоту имеют равные площади, следовательно, S∆_ABC=S∆_DBC . Заметим, что ∆ABC и ∆DBC имеют один общий элемент- ∆BOC, следовательно, если вычесть из площадей искомых треугольников площадь ∆BOC мы получим два, равных по площади треугольника. Значит, S∆_AOB=S∆_COD.

3. Рассмотрим ∆AOB и ∆BOC, они имеют общую высоту h1, но имеют различные основания, поскольку мы знаем, что площади треугольников имеющих общую высоты относятся как их основания:

4. Рассмотрим ∆AOD и ∆ COD, они имеют общую высоту h2, но имеют различные основания, поскольку мы знаем, что площади треугольников имеющих общую высоты относятся как их основания:

5. Правые части равенств (1) и (2) одинаковы, следовательно одинаковы и правые части:

 

Ответ: площадь трапеции равна .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

III Замечательные задачи

Планиметрические задачи с трапецией встречаются не только в 9 и 10 классе, но и в 11. Для того, чтобы в 11 классе решать более сложные задачи необходимо получить базовые знания ещё в самом начале изучения планиметрии. Необходимо ещё с самых азов стараться полностью вникнуть в суть предложенных в учебнике задач. Ведь именно они есть основа других задач, более сложных и увлекательных. А теперь после такого небольшого лирического отступления рассмотрим задачу, которая встретилась на  диагностической работе по математике в 11 классе.

Задача 5:Площадь трапеции ABCD равна 810. Диагонали пересекаются в точке O. Отрезки, соединяющие середину P основания AD с вершинами B и C, пересекаются с диагоналями трапеции в точках M и N. Найдите площадь треугольника MON, если одно из оснований трапеции вдвое больше другого.

Рассмотрим первый случай.

1.Пусть AD=2BC.

2. ABCP и BCDP – параллелограммы (по построению), поэтому M и N– середины BP и CP, значит, CM и BN -  медианы ∆BPC

3. Пусть h – высота трапеции, ВС=a, AD=2a, OM=x. Тогда

4.ОС=2х (т.к. О- точка пересечения медиан треугольника BPC), поэтому AM=MC=3x, OA=AM+OM=3x+x=4x

Аналогично, , значит, ∆ MON~∆AOD с коэффициентом подобия. Следовательно,

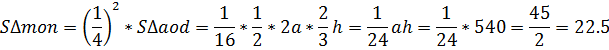
Рассмотрим 2 случай:

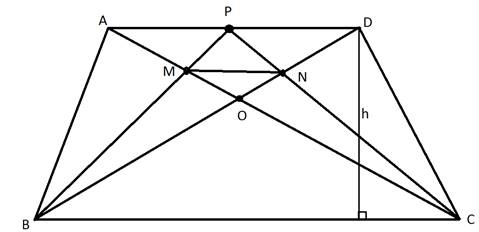
1.ПустьВС=2AD, h-  высота трапеции, AD=a, BC=2a, AM=3t.Тогда ah=540( см. 1 случай)

2.∆AOD~∆COB с коэффициентом подобия, а ∆AMP~∆CMB с коэффициентом подобия . Тогда,

, значит

Аналогично,

Следовательно,

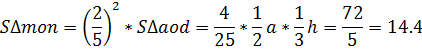
Ответ:S∆mon=22.5  или14.4

Задача 6

Я  не могла удержаться от соблазна представить моим слушателям решение одной  из самых красивых и простых  задач о трапеции . Она была представлена в методичке УРЭК « Трапеция. Некоторые методы решения задач»

Дано:

Диагонали трапеции равны 3 и 5 см , а отрезок, соединяющий середины оснований, равен 2 см . Найти площадь трапеции.

Решение

Выполним дополнительные построения: проведём отрезок CF, параллельный диагонали BD, проведём отрезок СКǁ MN.

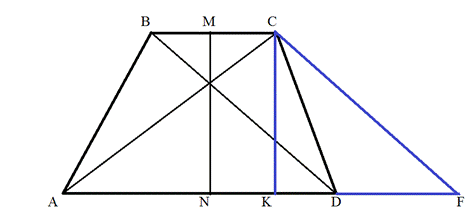
Получим параллелограммы MCKN и BCFD, следовательно, CK=MN, MC=NK , BC=DF , BD=CF. Тогда

Значит, СК- медиана треугольника ACF.

Докажем, что площадь исходной трапеции равна площади треугольника ACF.

Для вычисления площади треугольника ACF проведём следующие дополнительные построения: на прямой СК отложим КН=СК.

 Тогда ∆CKF=∆HKA ( по двум сторонам  и углу между ними). Поэтому AH=CF и площадь треугольника ACF равна площади треугольника ACH. По теореме обратной теореме Пифагора , убеждаемся, что треугольник АСН – прямоугольный. Находим его площадь

Ответ : S=6 см.

Это короткое и изящное решение приносит эстетическое удовольствие!

Задача 7

Дано:

В четырёхугольнике ABCD сторона АВ равна стороне ВС, диагональ АС равна стороне CD а ∟АСВ=∟ACD. Радиусы окружностей вписанных в треугольники АСВ и ACD, относятся как 3:4. Найдите отношение площадей этих треугольников.

Решение

Обозначим ∟АСВ=∟ACD=α. Прямые AB и CDпараллельны, так как ∟ВАС=∟АСВ=∟ACD, значит ABCD -  трапеция.

Высоты треугольников АВС и ACD, проведённые и з вершин соответственно С и А , равны, поэтому отношение площадей треугольников АВС и ACD равно отношению оснований АВ и CD трапеции.

Центры O и Q окружностей, вписанных в треугольники соответственно АВС и ACD, - точки пересечения биссектрис этих треугольников, поэтому ∟АСО=∟ACQ.

Пусть ОМ и QK – радиусы окружностей, проведённые в точки касания окружностей со стороной АС, N- середина основания AD равнобедренного треугольника ACD.

Прямоугольные треугольники CKQ и СМО подобны по двум углам, причём коэффициент подобия равен

Значит

Положим СК= 4х, СМ=3х. Точка М- середина основания АС равнобедренного треугольника АВС, поэтому

По теореме косинусов

Из прямоугольного треугольника ВМС находим, что

Значит, АВ=ВС= .Следовательно

Ответ : 9:14

Эта задача поистине прекрасна! В ней есть абсолютно всё: и подобие и и свойства фигур и даже тригонометрия!

А теперь напоследок мне хочется рассмотреть задачу по стереометрии, которая решается с помощью планиметрии. И как решается- просто блеск! Решение этой, казалось бы, сложной задачи оказывает весьма простым, но очень красивым.

Задача 8

Дано:

О- центр шара, вписанного в усечённый конус, ABCD- осевое сечение конуса, ОЕ┴CD , МК┴AD, MC=r, KD=R, OM=r_ш.

Доказать, что r ²_ш=R*r.

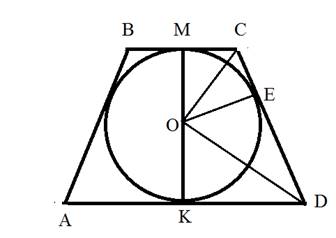
1.     Поскольку ОЕ┴ CD, то ОЕ=r_ш, поскольку радиус окружности - это перпендикуляр в точку касания.

2.      Отрезки касательных, проведённые и з одной точки равны, следовательно, МС=СЕ, KD=DE.

3.      Докажем что треугольник  OCD прямоугольный.

Во-первых, СО и DO биссектрисы по определению. Тогда пусть угол МСО=α , а угол KDO=β

Сумма односторонних углов при параллельных прямых BC и AD равна 180◦, то есть 2α+2β=180◦ ,следовательно α+β=90◦, следовательно треугольник  OCD прямоугольный.

4.     Рассмотрим треугольник OCD.

 ОЕ- высота в прямоугольном треугольнике , по определению ОЕ²=DE*EC, то есть r²_ш=R*r .

 ЧТД