Առնչություններ եռանկյան կողմերի և անկյունների միջև

Առնչություններ եռանկյան կողմերի և անկյունների միջև

    Եռանկյան ավելի մեծ կողմի դիմաց ընկած է ավելի մեծ անկյունը:

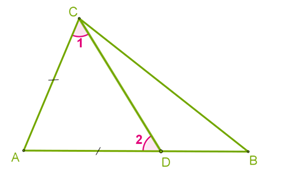
     Ապացույց:

    Դիցուք ABC եռանկյան մեջ AB կողմն ավելի մեծ է AC կողմից:

     Ապացուցենք, որ ∡C>∡B:

     Տեղադրենք AB կողմի վրա AC-ին հավասար հատված:

    Քանի որ AD<AB, ապա D կետն ընկած է A և B կետերի միջև:

    Հետևաբար, 1 անկյունը հանդիսանում է C անկյան մաս, և ուրեմն՝ ∡C>∡1

 2 անկյունը BDC եռանկյան արտաքին անկյունն է, ուստի ∡2>∡B

      ∡ 1=∡ 2՝ որպես ADC հավասարասրուն եռանկյան հիմքին առընթեր անկյուններ:

     Այսպիսով, ∡C>∡1=∡2>∡B    

     Այստեղից հետևում է, որ ∡C>∡B

     Տեղի ունի նաև հակառակ պնդումը.

     Եռանկյան ավելի մեծ անկյան դիմաց ընկած է ավելի մեծ կողմ:

    Հետևանքներ.

    Հետևանք 1.

    Եթե եռանկյան երկու անկյուններ հավասար են, ապա եռանկյունը հավասարասրուն է (հավասարասրուն եռանկյան հայտանիշ):

    Հետևանք 2.

    Եթե եռանկյան երեք անկյուններ հավասար են, ապա եռանկյունը հավասարակողմ է:

    Հետևանք 3.

    Ուղղանկյան եռանկյան ներքնաձիգն ավելի մեծ է էջից: