Վեկտորները տարածության մեջ

Վեկտորները տարածության մեջ

     Հարթաչափության դասընթացում տրված վեկտորի սահմանումը պահպանվում է նաև տարածության դեպքում:  AB վեկտորը (գրվում է ) A և B կետերով տրվող ուղղորդված հատված է, ընդ որում, առաջին կետը՝ A կետը, հանդիսանում է վեկտորի սկզբնակետը, իսկ  B-ն վերջնակետը:

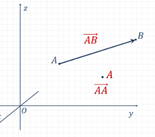
     Վեկտորները հաճախ նշանակում են նաև մի տառով՝ և այլն:

     և  երկու վեկտորներ կոչվում են համագիծ, եթե նրանք ընկած են զուգահեռ ուղիղների կամ միևնույն ուղղի վրա և տարագիծ՝ հակառակ դեպքում:

Եթե երկու ոչ զրոյական  և   վեկտորներ համագիծ են, ընդ որում AB և CD ճառագայթները համուղղված են, ապա և վեկտորները կոչվում են համուղղված,

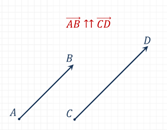
իսկ եթե ճառագայթները համուղղված չեն, ապա և վեկտորները կոչվում են հակուղղված:

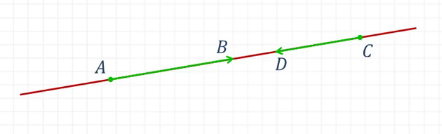
     Վեկտորները կոչվում են հավասար,  եթե նրանք համուղղված են, և նրանց երկարությունները հավասար են:

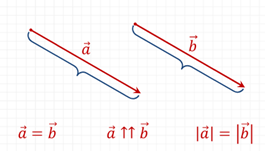
     Տարածության ցանկացած կետից կարելի է տեղադրել տրված վեկտորին հավասար միայն մեկ վեկտոր:

     Զրոյական վեկտորը, այսինքն 0 երկարությամբ վեկտորը, համարվում է ցանկացած վեկտորին համագիծ:

     –ն  վեկտորի երկարությունն է:

         հավասարությունը նշանակում է, որ  վեկտորը համագիծ է  վեկտորին և  , ընդ որում,  -ի ուղղությունը համընկնում է -ի ուղղության հետ, եթե  և ունի նրա հակադիր ուղղությունը, եթե

     Ցանկացած և վեկտորների համար և ցանկացած x և y թվերի համար տեղի ունեն հետևյալ հավասարությունները.

     Որպեսզի և  ոչ զրոյական վեկտորները լինեն համագիծ, անհրաժեշտ է և բավարար, որ գոյություն ունենա այնպիսի k թիվ, որ

   Նման կերպ, ինչպես հարթության դեպքում էր, սահմանվում է երկու վեկտորների գումարման գործողությունը՝

    Վեկտորների գումարման՝ հարթաչափության մեջ ուսումնասիրված հատկությունները տեղի ունեն նաև տարածության մեջ դիտարկվող վեկտորների համար: Վերհիշենք դրանք՝

:

    Երկու ոչ զրոյական վեկտորներ կոչվում են հակադիր, եթե նրանց երկարությունները հավասար են, և նրանք հակուղղված են:

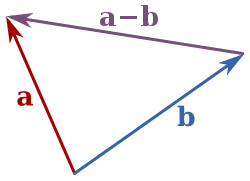
      և  վեկտորների տարբերություն կոչվում է այն վեկտորը, որի գումարը վեկտորի հետ հավասար է  վեկտորին:  և վեկտորների տարբերությունը կարելի է գտնել

բանաձևով, որտեղ -ն   վեկտորի հակադիրն է:

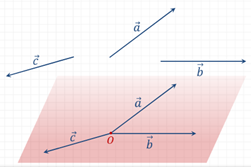
    և  երեք վեկտորներ տարածության մեջ կոչվում են համահարթ, եթե գոյություն ունի այդ երեք վերտորներին զուգահեռ հարթություն:

    Այլ կերպ ասած, վեկտորները համահարթ են, եթե գոյություն ունեն դրանց հավասար վեկտորներ, որոնք ընկած են մի հարթության մեջ, կամ որ նույնն է՝ եթե այդ վեկտորները կիրառենք (տեղադրենք) տարածության մի կետից, ապա դրանք կընկնեն մի հարթության մեջ:

    Երեք տարահարթ վեկտորների գումարը գտնելու համար կարելի է օգտվել զուգահեռանիստի կանոնից:

     Որպեսզի և  վեկտորները լինեն համահարթ, անհրաժեշտ է և բավարար, որ գոյություն ունենան x, y և z թվեր, որոնք միաժամանակ հավասար չեն 0, այնպես, որ

: