Պյութագորասի թեորեմը

Պյութագորասի թեորեմը

    Երկրաչափության ամենահայտնի թեորեմներից է Պյութագորասի թեորեմը, որի հայտնագործությունն ու ապացույցը վերագրվում է Պյութագորասին:

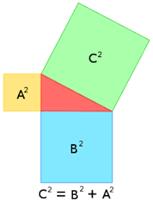
     Ուղղանկյուն եռանկյան ներքնաձիգի վրա կառուցված քառակուսու մակերեսը հավասար է նրա էջերի վրա կառուցված քառակուսիների մակերեսների գումարին:  

    Մաթեմատիկայի պատմության մեջ գոյություն ունեն պնդումներ այն մասին, որ այդ թեորեմը գիտեին դեռևս Պյութագորասից շատ առաջ: Մասնավորապես, եգիպտացիները գիտեին, որ 3, 4 և 5 կողմերով եռանկյունը ուղղանկյուն եռանկյուն է:  

Ներկայումս թեորեմը հնչում է այսպես՝

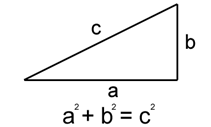
   Ուղղանկյուն եռանկյան ներքնաձիգի քառակուսին հավասար է եռանկյան էջերի քառակուսիների գումարին՝

   Հայտնի են այս թեորեմի բազմաթիվ ապացույցներ, սակայն ամենաակնառու ապացույցներից մեկը հիմնված է մակերեսների վրա:

   Տեղի ունի նաև Պյութագորասի թեորեմի հակադարձ թեորեմը, որը կիրառվում է որպես ուղղանկյուն եռանկյան հայտանիշ:

   Եթե եռանկյան մի կողմի քառակուսին հավասար է մյուս երկու կողմերի քառակուսիների գումարին, ապա այդ եռանկյունը ուղղանկյուն եռանկյուն է:

    Օրինակ

   Արդյո՞ք  8 սմ, 7 սմ և 9 սմ կողմերով եռանկյունը ուղղանկյուն եռանկյուն է: 

Ընտրում ենք մեծ կողմը և ստուգում Պյութագորասի թեորեմի տեղի ունենալը՝

Հետևաբար, եռանկյունը ուղղանկյուն չէ:

   Արդյո՞ք 5 սմ, 12 սմ և 13 սմ կողմերով եռանկյունը ուղղանկյուն եռանկյուն է: 

Ընտրում ենք մեծ կողմը և ստուգում Պյութագորասի թեորեմի տեղի ունենալը՝

169=144+25

    Հետևաբար, եռանկյունը ուղղանկյուն է: