Методические рекомендации к уроку

Тема урока "Числовые равенства и их свойства"

Цели обучения:

6.2.2.1

знать и применять свойства верных числовых равенств;

Критерии оценивания

Учащийся:

знает:

·         определение числового равенства;

·         свойства числовых равенств;

·         понятие о верных и неверных числовых равенствах;

умеет:

·         выполнять действия над числовыми равенствами, применяя их свойства.

Теоретический материал

Числовое равенство – это равенство, в обеих частях которого находятся числа и/или числовые выражения.

Основные свойства числовых равенств это: свойство рефлексивности, свойство симметричности, свойство транзитивности.

Дополнительные свойства числовых равенств это свойства действий над верными числовыми равенства. Числовое выражение в общем виде можно определить так:

1. Каждое число является числовым выражением.

2. Если А и В – числовые выражения, то (А) + (В); (А) – (В); (А) × (В): (А) : (В) тоже являются числовыми выражениями.

Число, полученное в результате выполнения всех указанных в числовом выражении арифметических действий, называют значением числового выражения.

a=a.

Если a= b, то b= a.

Если a= b и b= c, то a= c.

Если a= b, то a+c=b+ c.

Если a= b, то a⋅c= b·c.

Если a= b и с≠0, то a:c= b:c.

Если a = b,  a≠0  и b≠0, то 1a=1b.

Если a = b и c = d, то a⋅c= b·d.

Если a = b, то aⁿ = bⁿ.

Ход урока

Организационный момент. Актуализация опорных знаний.

Проверить домашнее задание.

Решить задания на повторение.

Приложение 1.

1. Найти значение произведения

А. .     В. .      С. .    D. .     Е. .

2. Найти значение выражения .

А. .     В. .    С. .     D. .   Е. .

3. Найти значение выражения  равно:

А. -23.        В. 23.      С. 37.           D. 21.          Е. -37.

4. Найти значение выражения  равно:

А. 19.         В. 5.           С. 3.            D. 9.            Е. 11.

5. Найти значение выражения 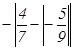 равно:

А. .   В. .     С.    D. .     Е. .

Совместно с учащимися определить тему и цели урока, "зону ближайшего развития".

Работа с классом. Разобрать примеры и обобщить понятия и свойства по теме.

Числовое равенство состоит из чисел, знака равенства и может содержать знаки действий и скобки.

Числовые равенства могут быть верными и неверными.

Число, полученное в результате выполнения всех указанных в числовом выражении арифметических действий, называют значением числового выражения.

К обеим частям верного числового равенства 22 - 6 = 24 - 8 прибавьте одно и то же число:

1) 8 2) 4.

Что получилось? (какие – верные или неверные равенства получились?)

Какой вывод можно сделать? (учащиеся формулируют вывод)

Свойство 1. Если к обеим частям верного числового равенства прибавить одно и то же число, то получим верное числовое равенство. Если a= b , то a+c = b+c

2) Обе части верного числового равенства 22 - 12 = 24 – 14 умножьте на одно и то же число: 1) 10 2) 2.

Проведите аналогичные размышления. (Какие – верные или неверные – равенства получились? Какой вывод можно сделать?)

Свойство 2. Если обе части верного числового равенства умножить или разделить на одно и то же число, то получим верное числовое равенство. Если a= b , то a ∙ c = b ∙ c;

а:с = b:с

Как из двух верных числовых равенств 22 – 9 = 24 – 11 и 24 – 11 = 45 – 32 получили числовое равенство 22 – 9 = 45 – 32

Какой вывод?

Свойство 3. Если a= b , b = с , то a = c.

Групповая работа. Объединить учащихся в разноуровневые малые группы. Раздать каждой группе карточки с заданиями.

Приложение 2

1) Составьте верные числовые равенства, используя изученные свойства.

2) Известно, что 5а = 15 и 3b = 6. Прибавьте к обеим частям равенства число 2:

5а+2 = 17 и 3b + 2 = 8
3) Известно, что 2а = 10 и 4b = 8. Прибавьте к обеим частям равенства число ( -2):

2а - ­2 = 8 и 4b-­2 = 6
4) Умножьте обе части равенства на 2:
а) 10а = 30 и 6b = 12;
б) 4а = ­20 и ­8b = ­16.
Учитель проходит по рядам, слушает, при необходимости задает дополнительные вопросы, корректирует решения учащихся, проверяет и оценивает похвалой работу групп, оказывает помощь слабоуспевающим.

Предоставить учащимся достаточно времени для выполнения заданий.

Проверить правильность ответов, провести анализ ошибок. Выслушать выводы учащихся по заданиям.

Каждая группа демонстрирует свой результат выполнения заданий.

Старший группы оценивает вклад каждого, выставляя отметку.

Индивидуальная работа. Для закрепления и оценки усвоения пройденного материала предложить учащимся задания. Каждый выполняет самостоятельно.

Приложение 3

I) Запишите верное числовое равенство, которое получится, если обе части равенства: 1)1,2∙(-7)= -8,4  умножить: а) на (-5); б) на 3;в) на 6

Ответ: 1.а.-8,4 = -8,4

-8,4 ∙ (-5) = -8,4 ∙ (-5)

42 = 42

б.-8,4 = -8,4

-8,4 ∙ (3) = -8,4 ∙ (3)

 -25,2 = - 25,2

в.-8,4 = -8,4

-8,4 ∙ (6) = -8,4 ∙ (6)

-50,4 = -50,4

2)5,4∙2=10,8  разделить: а) на-3; б) на 9;в) на 6

2. Получаем выражение: 10,8 = 10,8, каждую часть делим на нужное число, в результате получаем:

а. -3,6 = -3,6

б. 1,2 = 1,2

в. 1,8 = 1,8

II) Используя свойство верных числовых равенств: а = b и b = c, то a = c, из данных выражений составьте все возможные верные равенства:

1) 3² ∙8 ; 14,4:0,2 ; 100-28;

Ответ: 1) 3² ∙8 =14,4:0,2;

3² ∙8 =100-28

14,4:0,2=100-28

2)15∙1,4; 2³+13; 8,4 : 0,4

Ответ: 2) 15∙1,4= 2³+13;

15∙1,4= 8,4 : 0,4;

2³+13=8,4 : 0,4

3) 2,5∙12 ; 4,5:0,15 ; 8∙3+6

Ответ: 3) 2,5∙12 = 4,5:0,15;

2,5∙12 = 8∙3+6;

4,5:0,15 =  8∙3+6

все возможные равенства 

III) Используя свойства верных числовых равенств запишите верное числовое равенство которое получится если
1) к обеим частям равенства 3,6∙(-4)=72:(-5)
прибавить число а) -5,6; б) число
2)Обе части равенства 2,4 -12,9 = 63:(-6) умножить а) на -4; б) на 2.

Ответ:

1) а) 3,6∙(-4)-5,6 = 72:(-5)-5,6                      -20 = -20
б) 3,6∙(-4)+= 72:(-5)+                  -14,4+4,4 = -14,4+4,4 , -10 = -10
2) а) (2,4 -12,9)∙(-4) = 63:(-6)∙(-4)                    42 = 42
б) ( 2,4 -12,9)∙2 = 63:(-6) ∙2                          -21 = -21

IV) Запишите верное числовое равенство, которое получится, если к обеим частям данного равенства прибавить:

а) 1,3; б) -1,8; в) -11

1) 7,2+1,8=9                           

7,2+1,8+1,3=9+1,3                  7,2+1,8-1,8=9-1,8                     7,2+1,8-11=9-11

10,3 = 10,3                                 7,2 = 7,2                                      -2 = -2

2) 1,4∙5=7

1,4∙5+1,3 = 7+1,3                      1,4∙5-1,8 = 7-1,8                          1,4∙5-11 = 7-11                     

8,3=8,3                                      5,2=5,2                                     -4=-4

3) 6-1,3=4,7

6-1,3+1,3=4,7+1,3                   6-1,3-1,8=4,7-1,8                      6-1,3-11=4,7-11

6=6                                          2,9=2,9                                      -6,3=-6,3

V) Запишите верное числовое равенство, которое получиться, если обе части равенства умножить: а) на -5; б) на 3; в) на 0,5

1) а) 1,2 ∙ (-7) =-8,4

1,2 ∙ (-7) ∙ (-5) =-8,4 ∙ (-5)

42=42

б) 12 ∙ (-7) =-8,4,

1,2 ∙ (-7) ∙ 3 =-8,4 ∙ 3

-25,2=-25,2

в) 1,2 ∙ (-7) =-8,4

1,2 ∙ (-7) ∙ 0,5 =-8,4 ∙ 0,5

4,2=4,2

VI) Запишите верное числовое равенство, которое получится, если к обеим частям данного равенства прибавить:

а) 1,3; б) -1,8; в) -11

4) 9:1,8=5                           

9:1,8+1,3=5+1,3                     9:1,8-1,8=5-1,8                         9:1,8-11=5-11

6,3=6,3                                   3,2=3,2                                      -6=-6

VII) Запишите верное числовое равенство, которое получиться, если обе части равенства умножить: а) на -5; б) на 3; в) на 0,5

а) 5,4 ∙ 2 =10,8

5,4 ∙ 2 ∙ (-5) =10,8∙ (-5)

54=54

б) 5,4 ∙ 2 =10,8

5,4 ∙ 2 ∙ 3 =10,8 ∙ 3

32,4=32,4

в) 5,4 ∙ 2 =10,8

5,4 ∙ 2 ∙ 0,5 =10,8 ∙ 0,5

5,4=5,4

После окончания выполнения, попросить обменяться тетрадями соседей. Взаимопроверка по ключу. Собрать информацию о выполнении. Разобрать примеры при решении которых были затруднения.

Беседа. Рефлексия.

Домашнее задание.  Знать определения, решить из уровня В учебного пособия "Математика 6" №...№.

На уроке предусмотрена дифференциация в виде работы в разнородных парах (разного уровня обучаемости).

Предусмотрена взаимопроверка по ключу, в ходе которой оценивается умение учеников применять теоретические знания. В ходе групповой деятельности при выполнении задании оцениваются умение находить результат, а также решать задания по теме, опираясь на понятие и свойства, изученные на данном уроке и прошлый опыт.

Запланированы виды деятельности на уроке, способствующие передвижению учащихся по классу, поэтому необходимо обеспечить безопасность. Следить за осанкой учащихся.

Литература:

"Математика 6", Абылкасымова А.Е., Кучер Т.П., Жумагулова З.А.;

"Математика 6", Алдамуратова Т.А, Байшоланов Т.С.;

Самостоятельные и контрольные работы, Ершова А.П., Голобородько В.В. 

Интернет ресурсы:

http://www.yaklass.ru

https://school-assistant.ru